Whether teaching remedial, mainstream, or honors classes, in a segregated or integrated program, these interactive animations bring to life algebra/geometry topics from pre-algebra through pre-calculus. Algebra In MotionTM animations have a basic license for 4 on-site computers at 1 school to use at a variety of levels (other licenses are available instead). They perform equally well on either the Windows or Macintosh platform. Although a detailed instruction manual is included (PDF format), most of the animations can be successfully run simply using the on-screen information.
NOTE: The animations are data files written in The Geometer’s Sketchpad, so Sketchpad must reside on your computer for the files to run – see full explanation in “Requirements” on the home page.
Galleries below are titled:
The Basics
Introducing the Coordinate Plane & Graphing
Multiplication & Factoring
Geometry
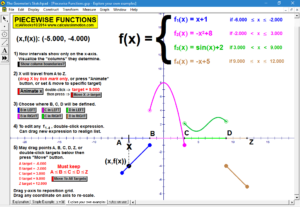
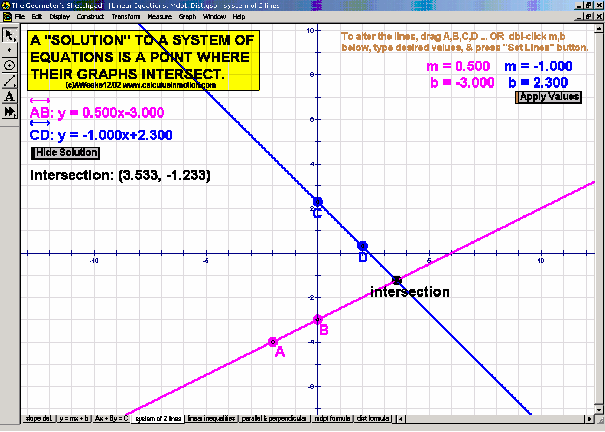
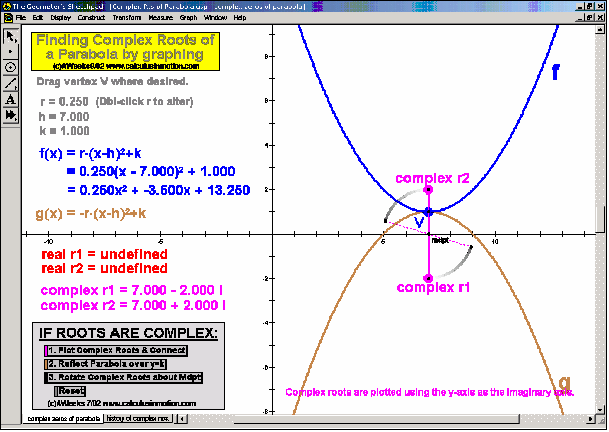
Connecting Solutions to Graphs
Advanced Graphing
Conics & Their Applications
Trigonometry
Theorems
More Applications & Vertical Teaming
THE BASICS
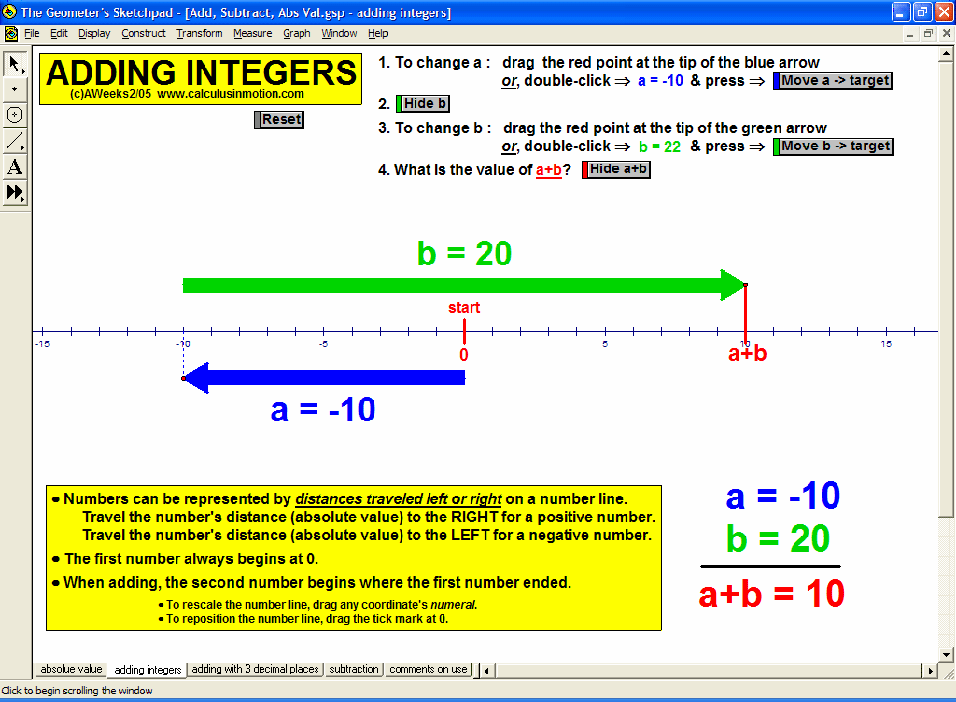
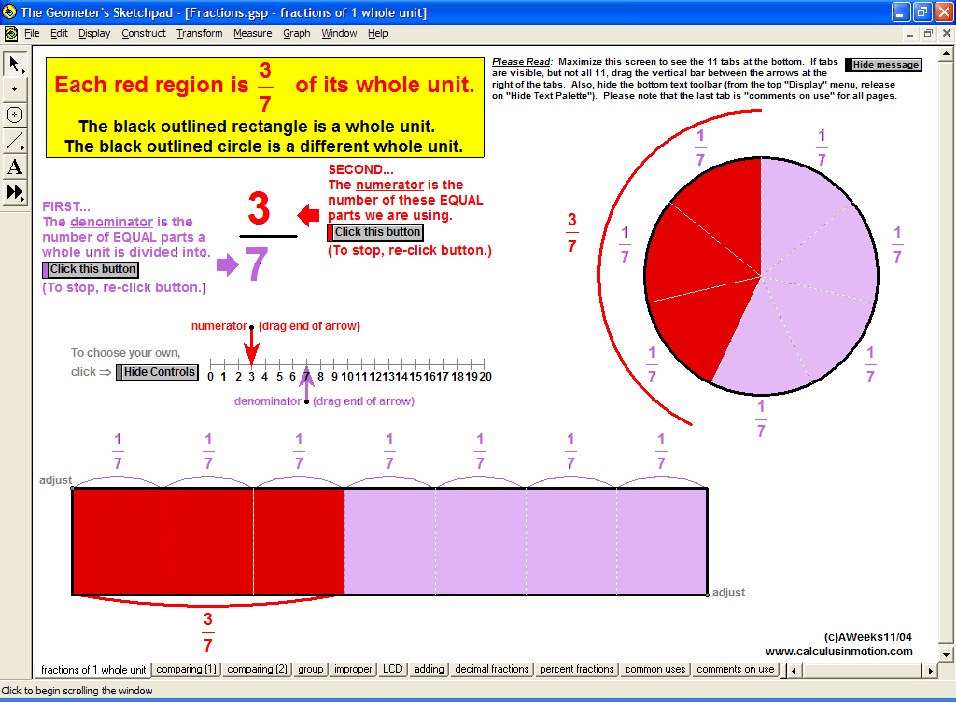
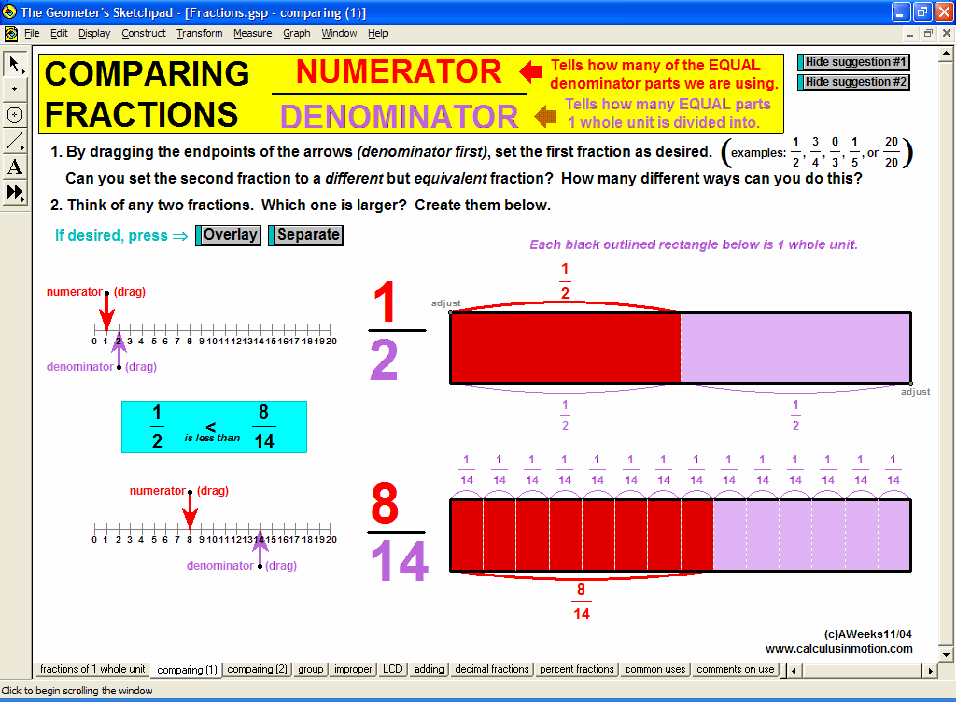
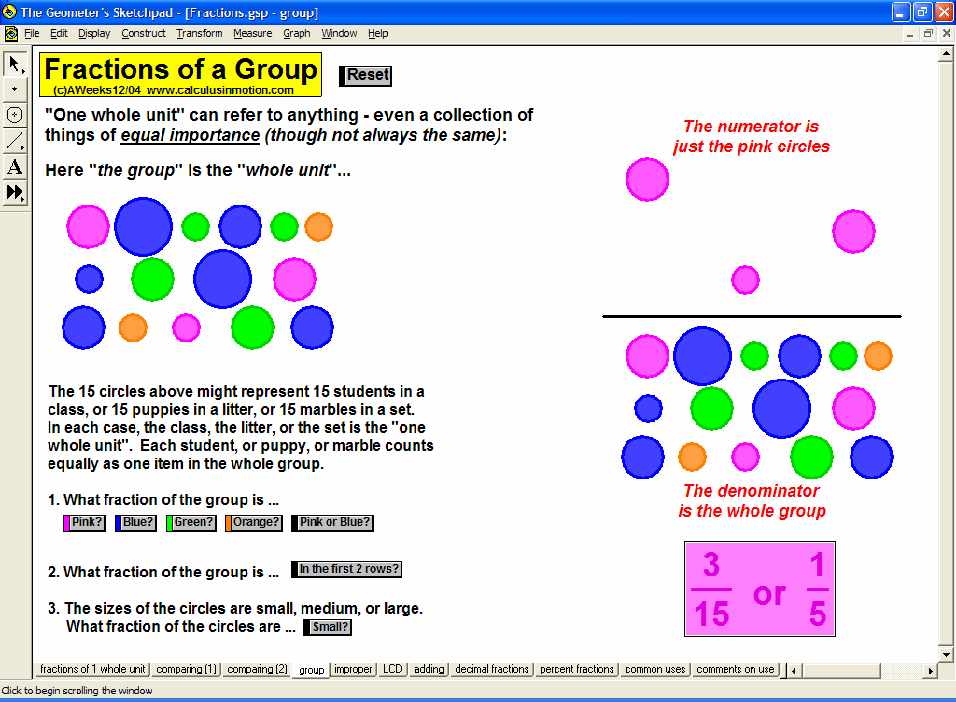
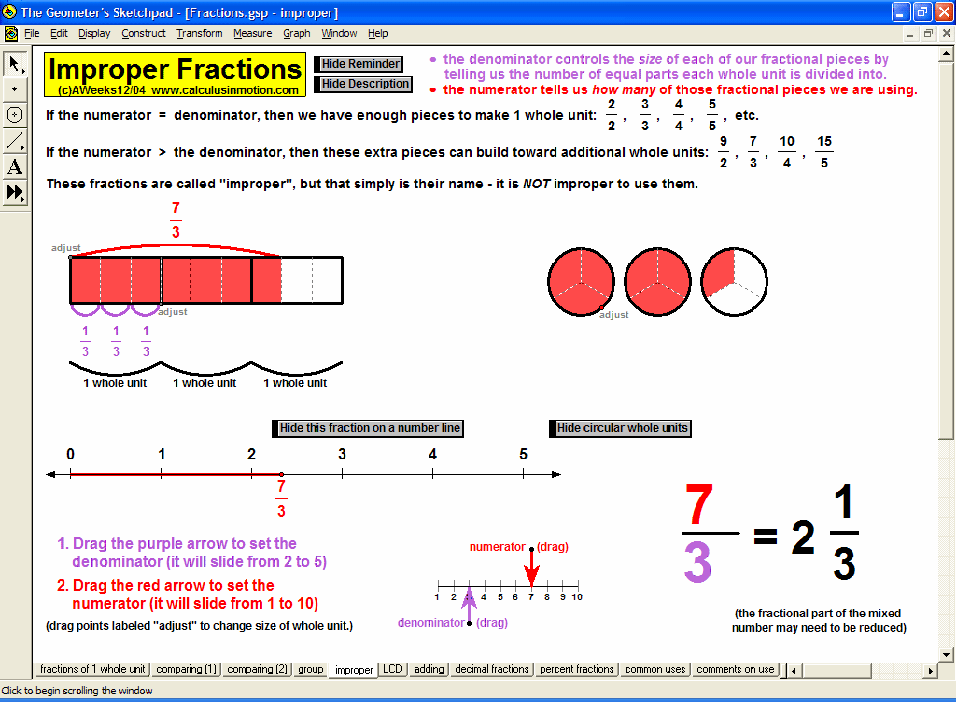
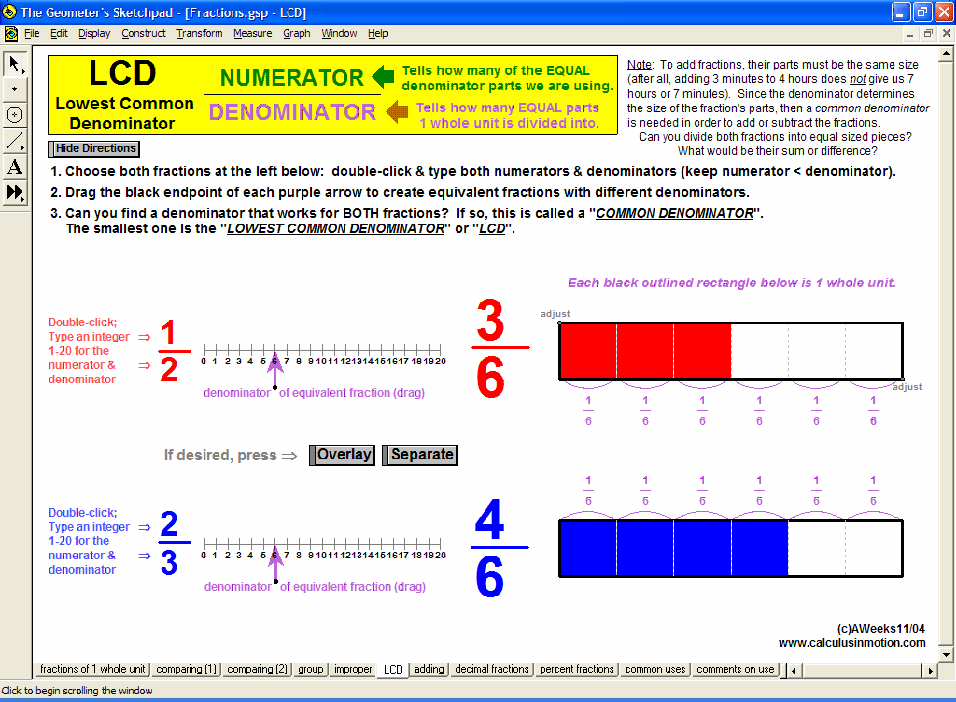
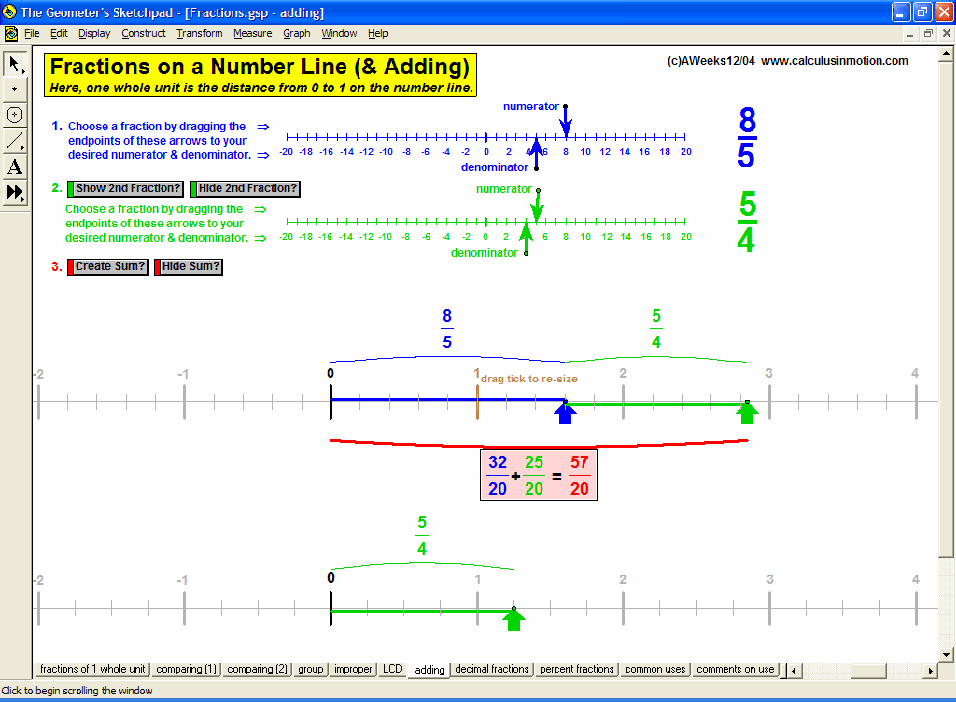
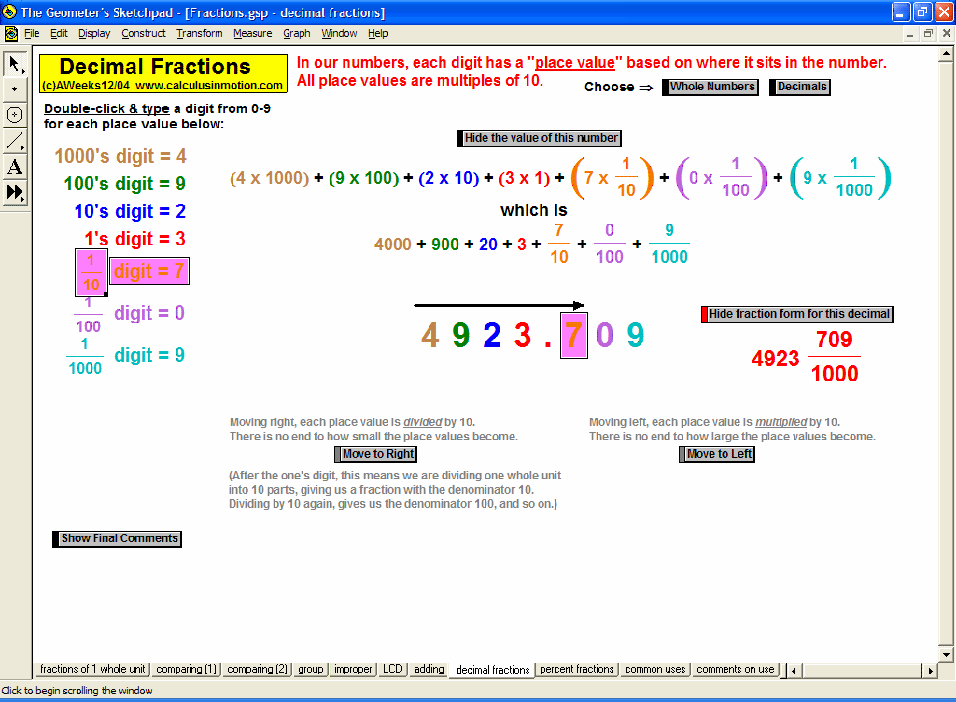
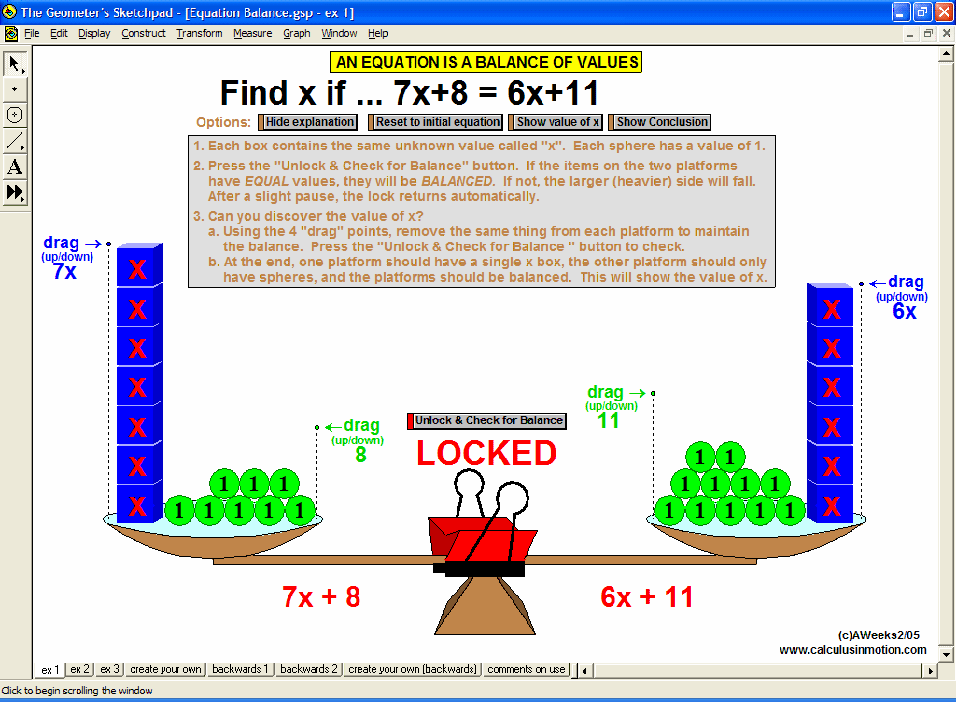
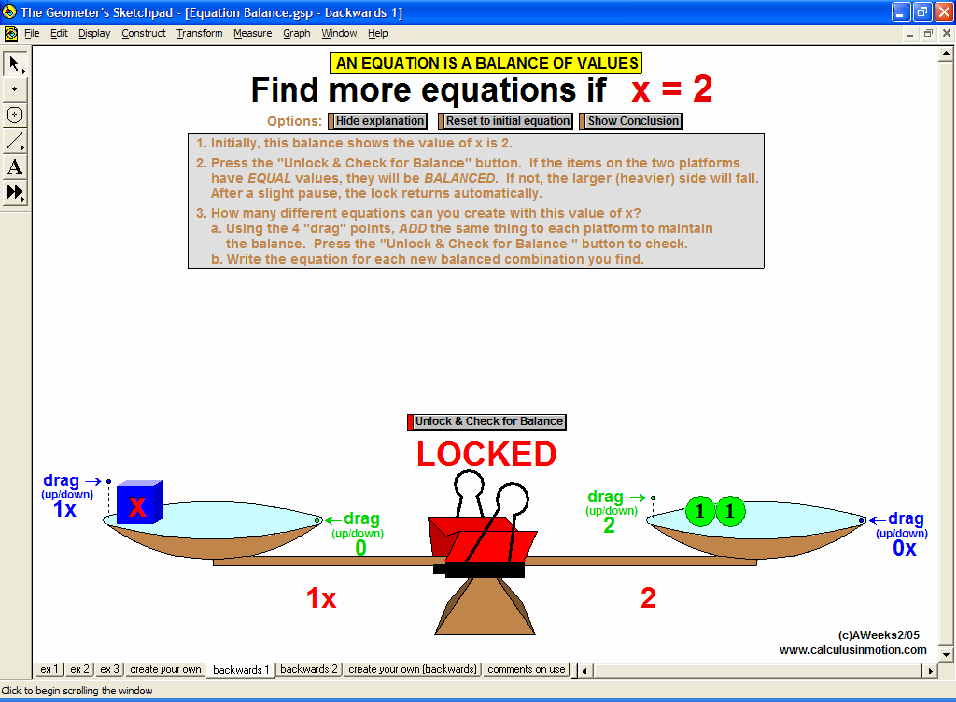
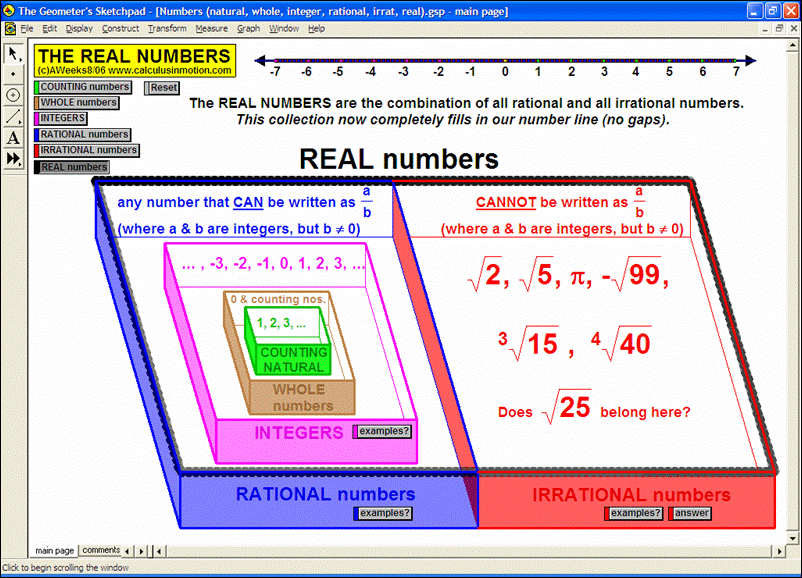
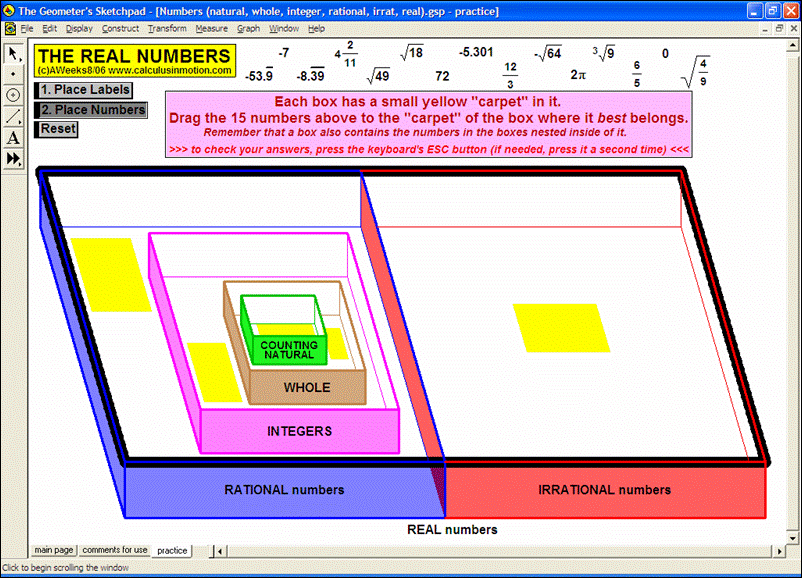
Visually explore or review fractions (meanings, comparisons, improper, LCD, adding, decimals, percents), signed number operations, absolute value, and introduce the concept of an equation as a balance of values and use that balance to solve preset equations or create your own.
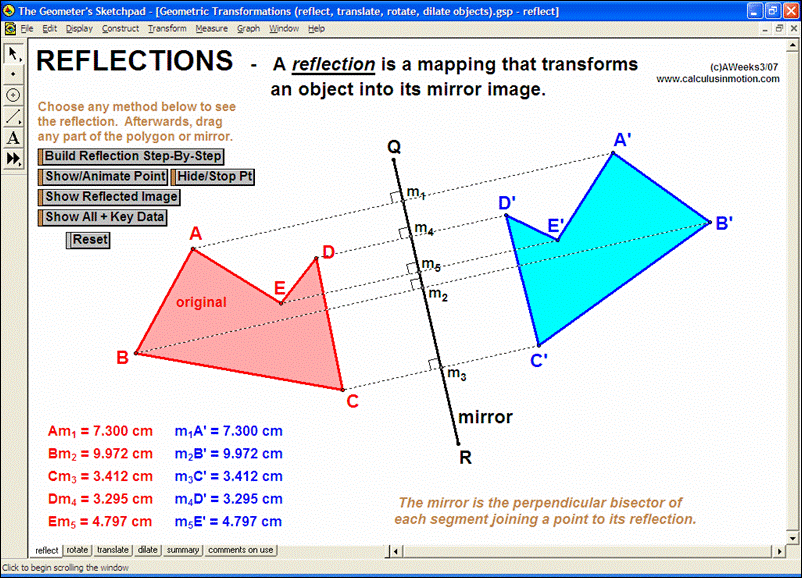
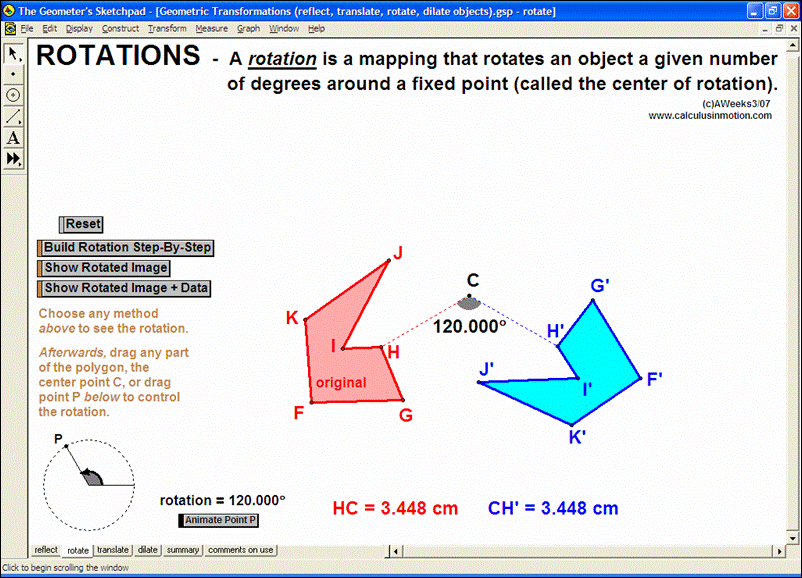
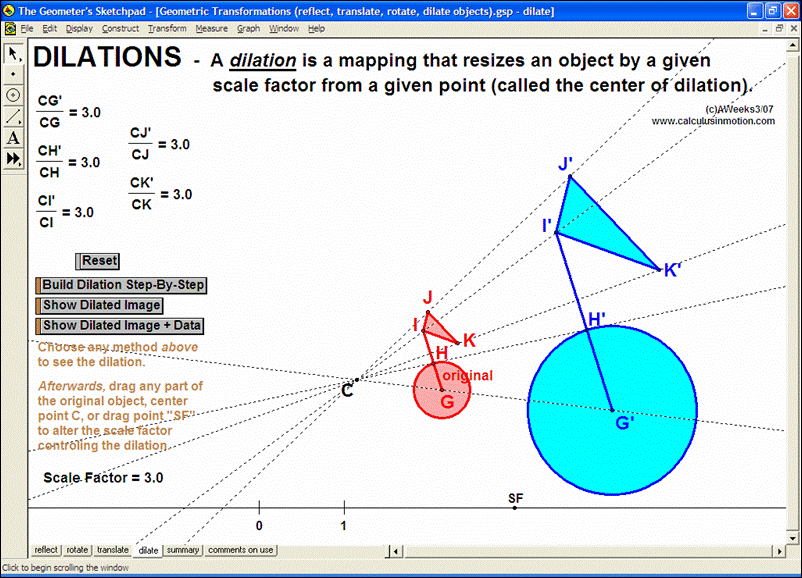
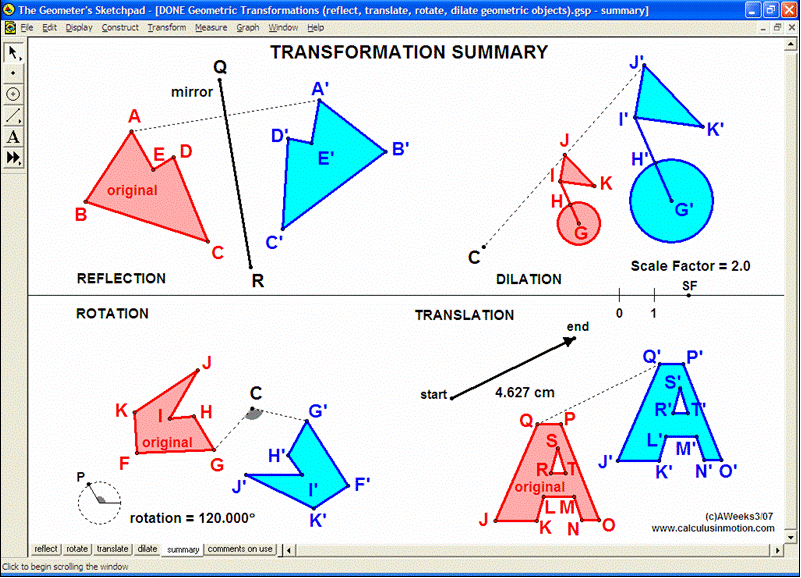
Geometric Transformations – Translate, Reflect, Rotate, Dilate, Summary, and an example using reflection
INTRODUCING THE COORDINATE PLANE & GRAPHING
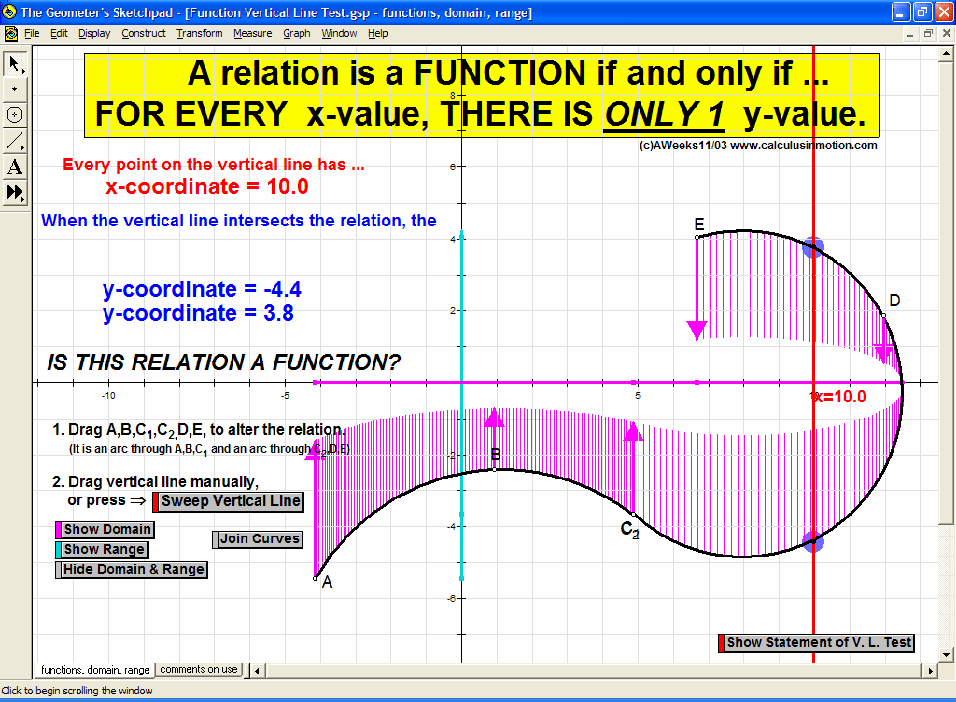
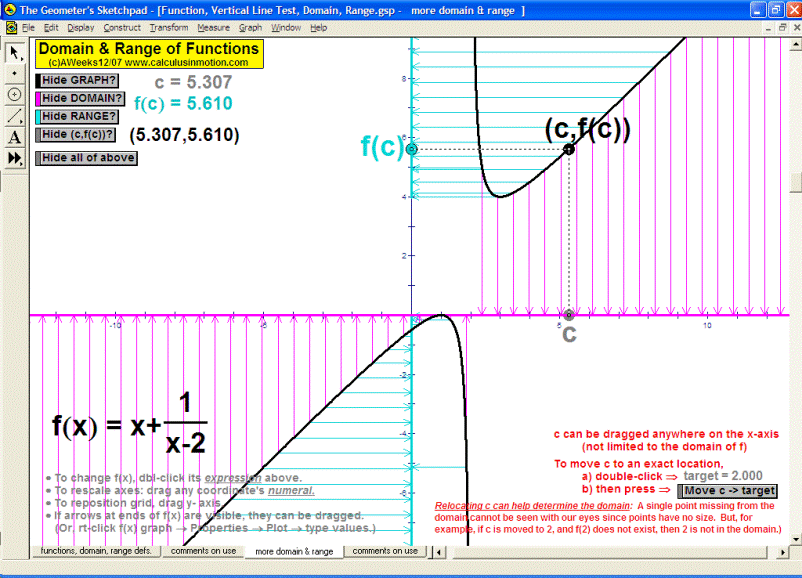
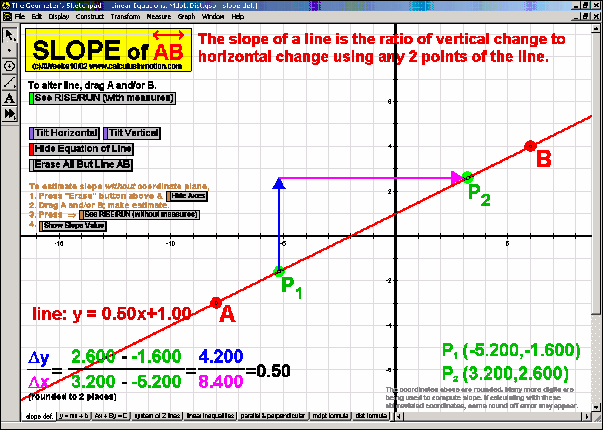
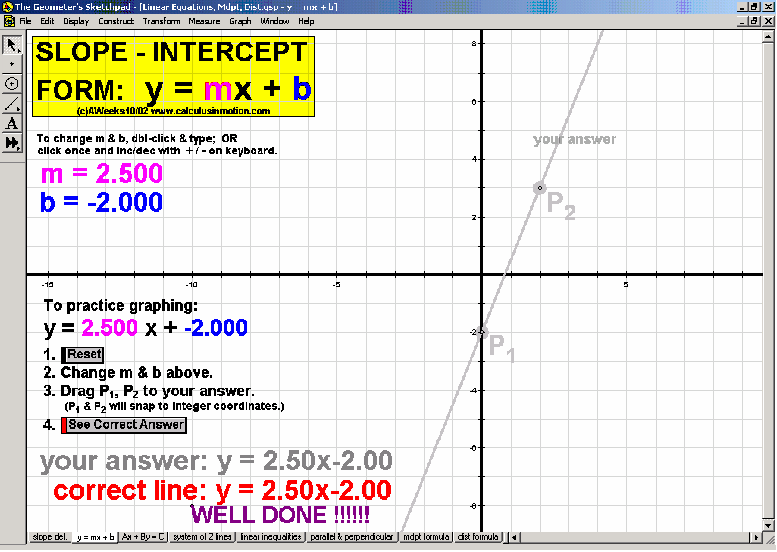
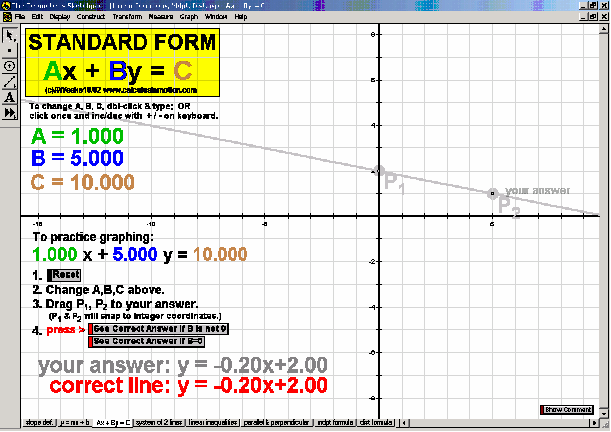
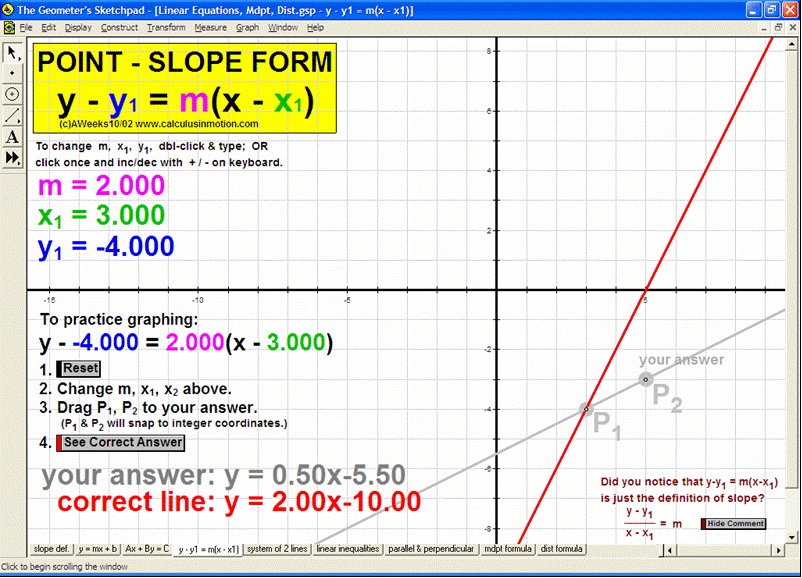
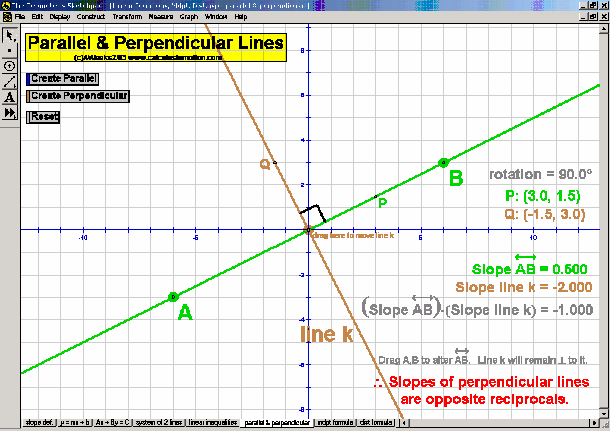
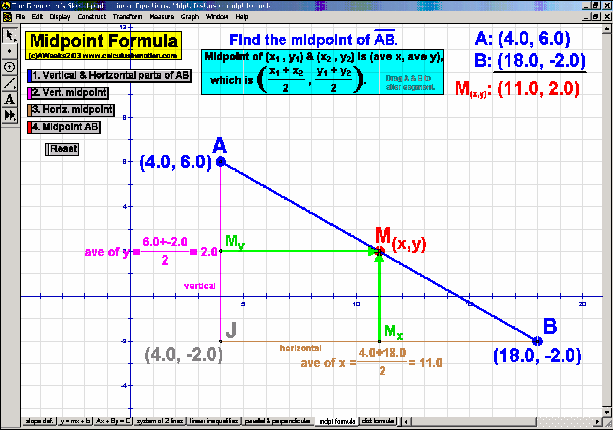
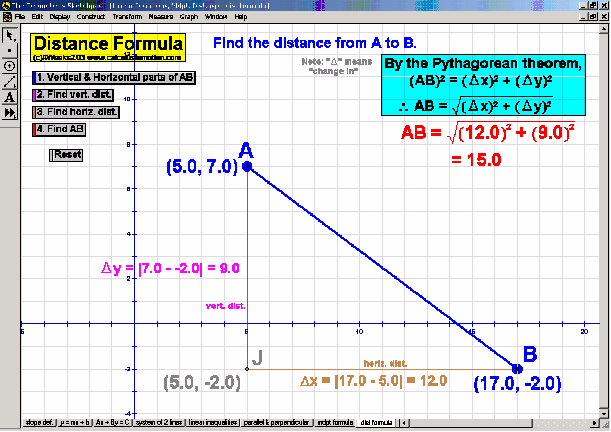
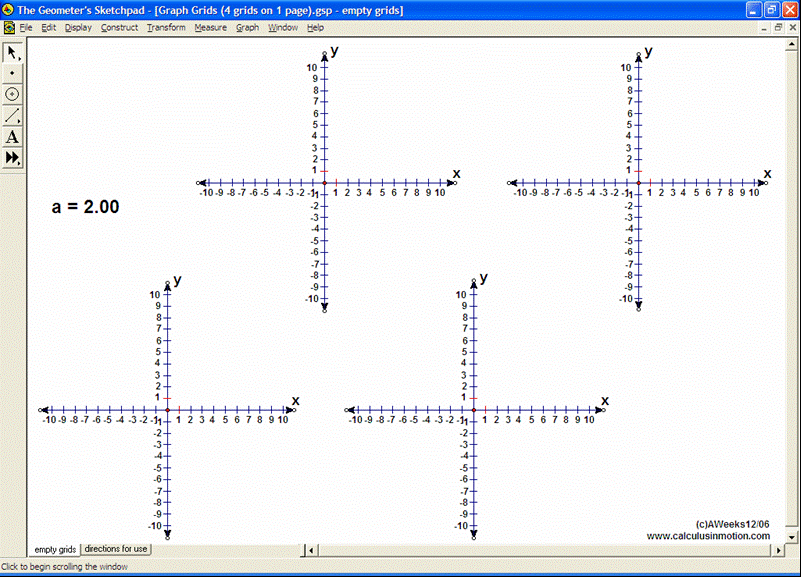
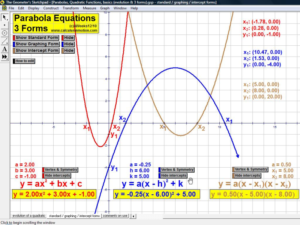
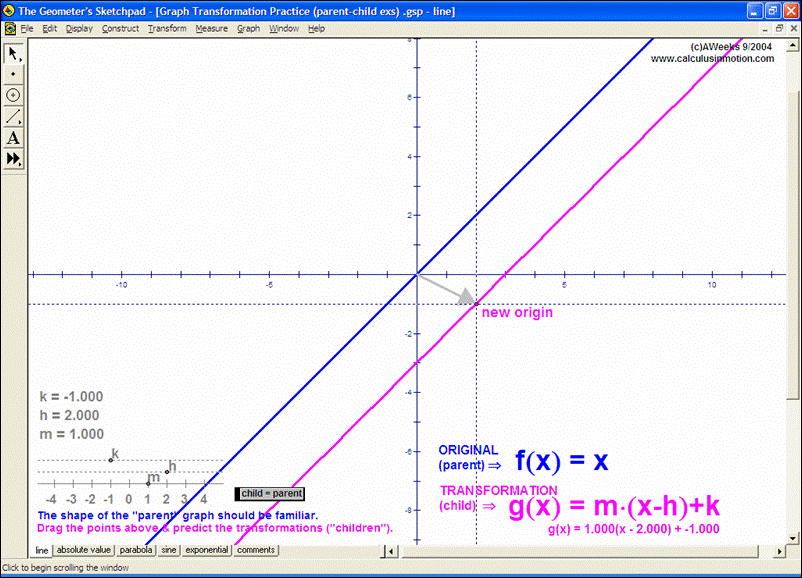
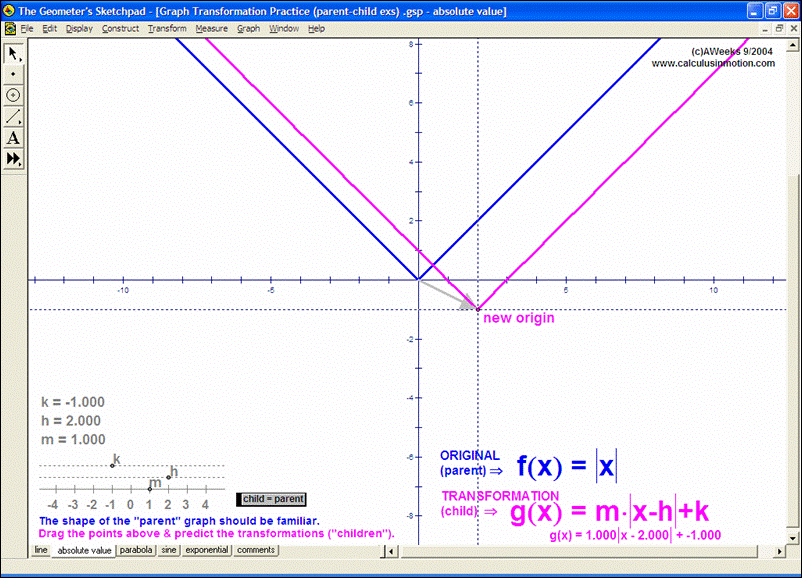
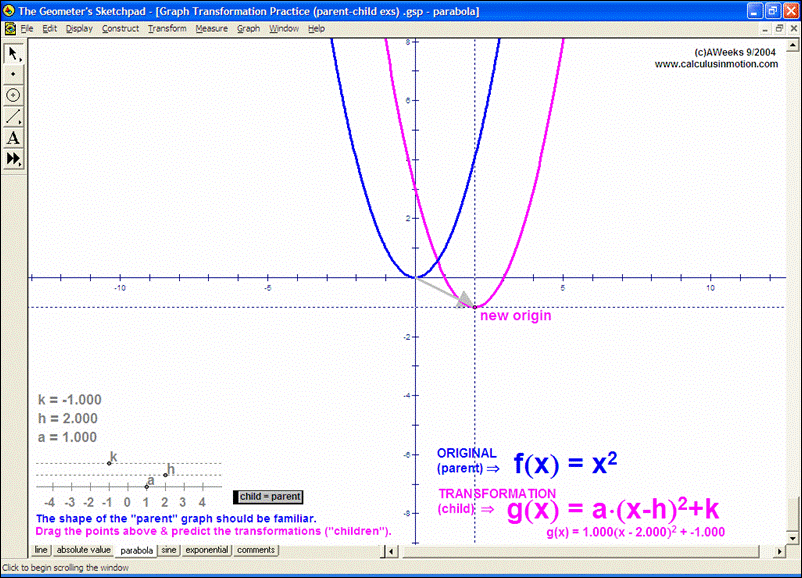
Introduce students to the basic vocabulary and characteristics of the coordinate plane (+ history). Dynamically display the definition of slope. Practice graphing lines from y = mx+b, Ax+By = C, and y-y1 = m(x-x1) forms. Explore the relationship of parallel and perpendicular lines to slope. Develop the formulas for midpoint and distance. Test relations using an animated vertical line test. Present 4 different graphing grids on the same screen.
MULTIPLICATION & FACTORING
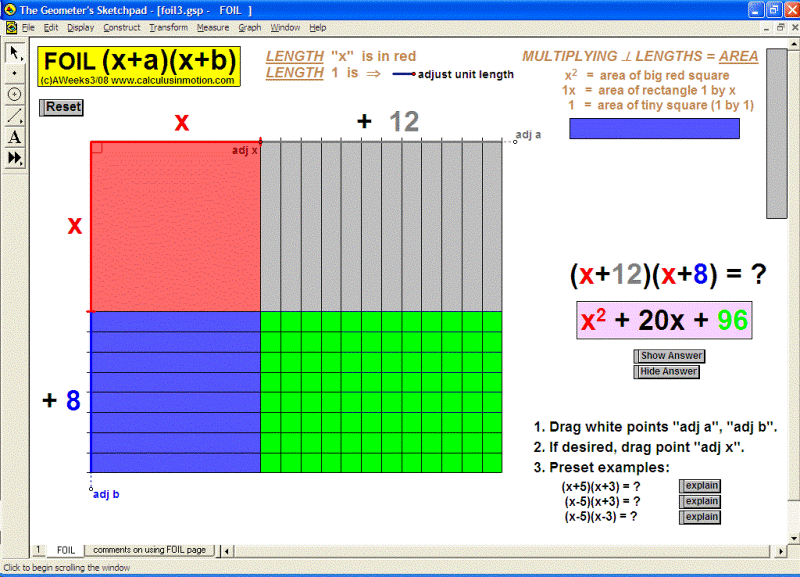
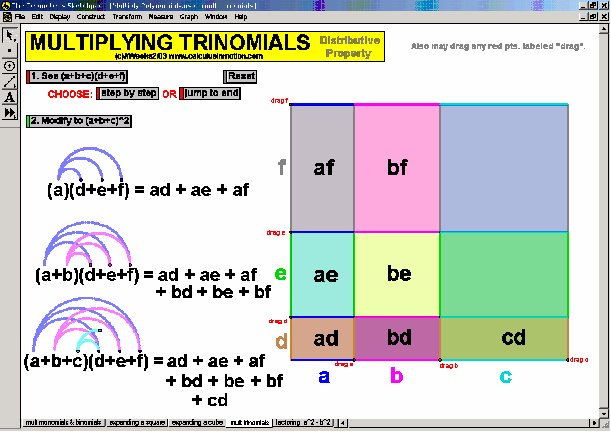
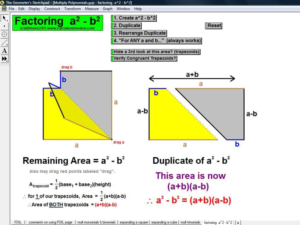
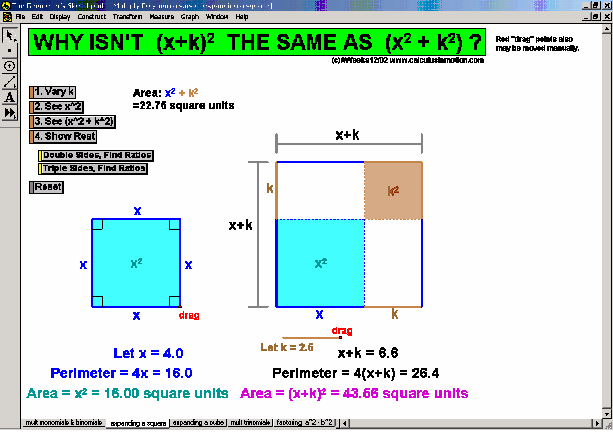
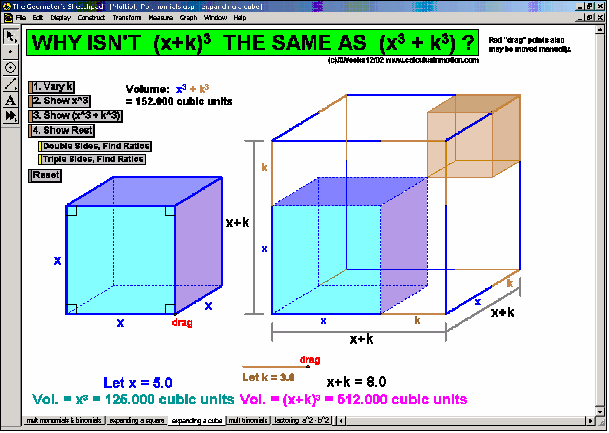
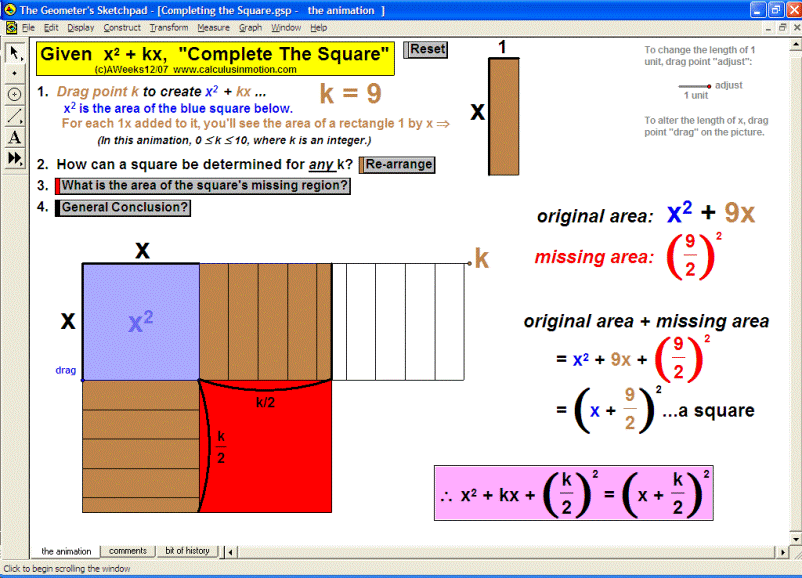
The distributive property is geometrically demonstrated for products of all combinations of monomials, binomials, and trinomials. The factored form of a2 – b2 is developed and proved. Special emphasis is given to (x+h)2 ≠ x2+h2 and (x+h)3 ≠ x3+h3. “Completing the square” is modeled physically.
GEOMETRY – added in 2016
ANGLES
definitions of all types of single angles and angle pairs, including all transversal angles
TRIANGLES
all parts and definitions; the 180 degree sum; the Exterior Angle Theorem; SSS, ASA, AAS, and SAS; the Isosceles Triangle Theorem;
visualizing overlapping triangles; altitudes, medians, and angle bisector segments along with the centers they determine and the characteristics of the loci of those centers including the Euler Line and the 9-point circle; the Triangle Inequality Theorem; the Geometric Mean; 30-60-90 degree triangles; and 45-45-90 degree triangles
CIRCLES
all parts and definitions; the circle’s equation in the coordinate plane; major vs. minor arcs & semicircles; central angles; inscribed angles; angles whose vertices are in the interior or exterior of the circle; quadrilaterals inscribed in circles; chord, secant, tangent properties and theorems; rolling out pi; arc lengths and sector areas; plus a few extra explorations for students who need a bit of a challenge
QUADRILATERALS, POLYGONS, SOLIDS
definitions and properties of each in the “family” of quadrilaterals (trapezoid, parallelogram, rhombus, rectangle, square) plus a summary;
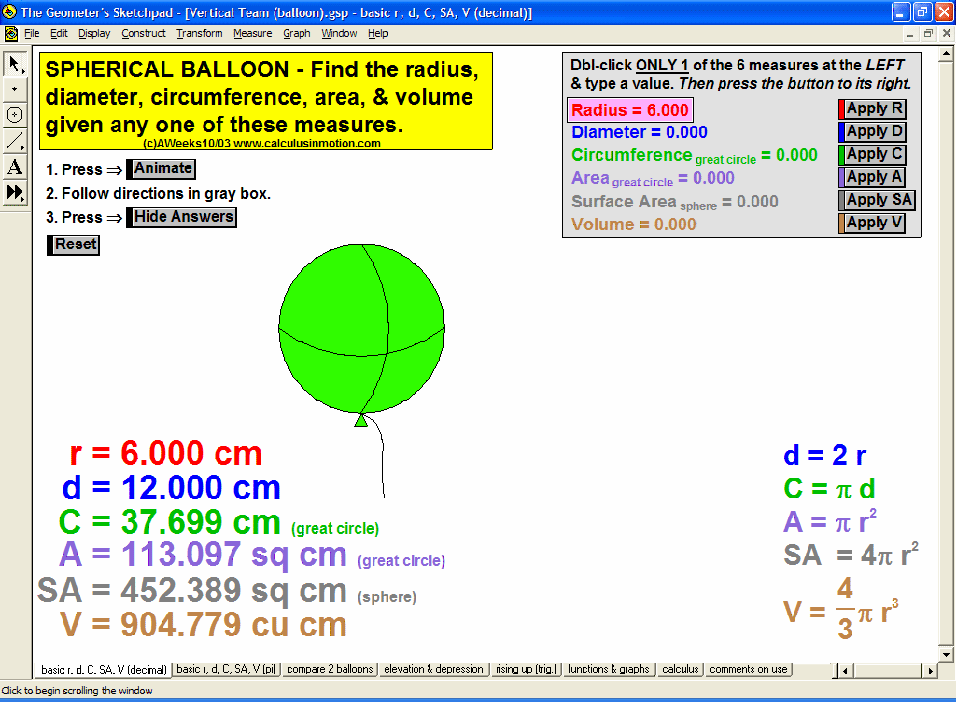
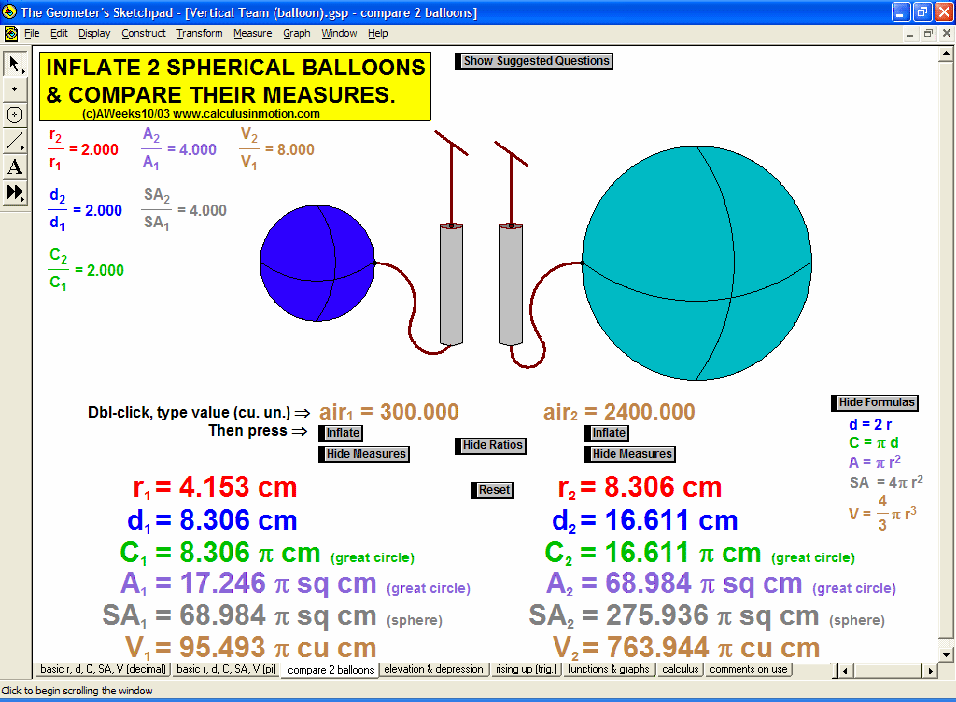
sums of interior and exterior angles in polygons; regular n-gons; all area formulas; definitions, properties, volumes and surface areas of prisms, cylinders, pyramids, cones, and spheres
For a quick view of these 40 new geometry-specific animations added to the Algebra In Motion collection in 2016, see them in action in the “GEOMETRY” video accessible from the “Videos” link in the menu bar.
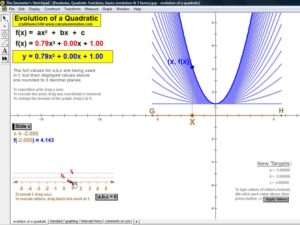
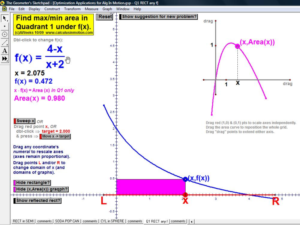
CONNECTING SOLUTIONS TO GRAPHS
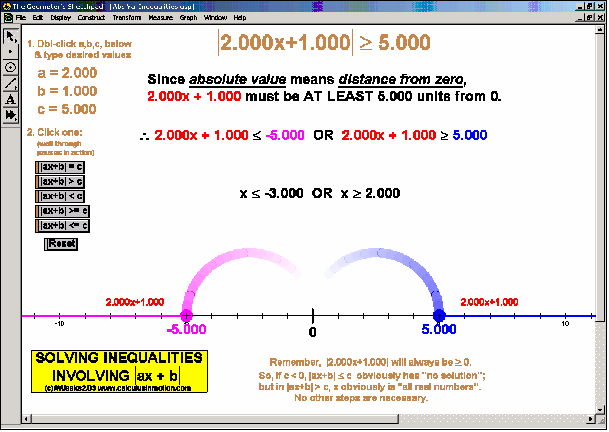
Reinforce meaningful understanding of solutions to sentences with absolute value, systems of 2 linear equalities or inequalities, and finding the roots of a quadratic equation (including complex roots) using its related parabola.
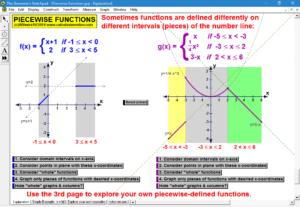
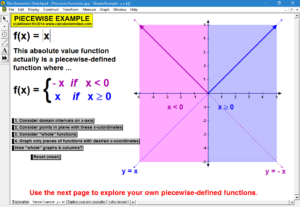
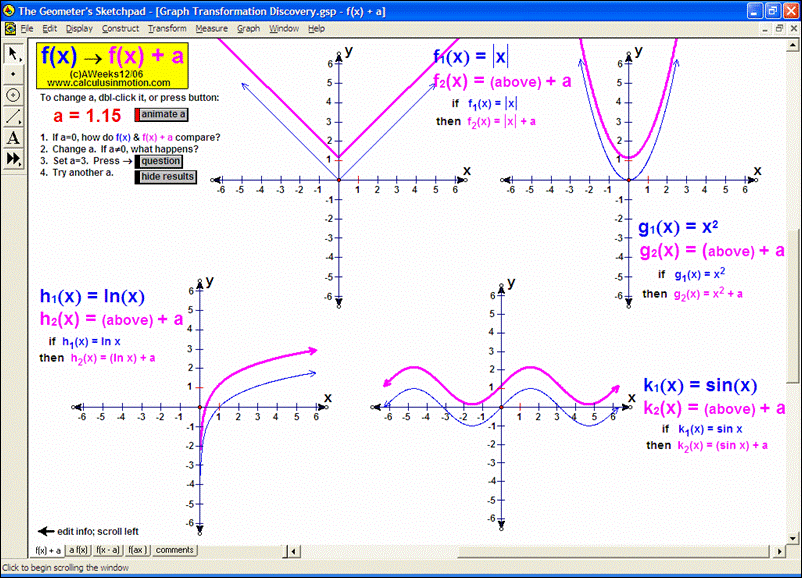
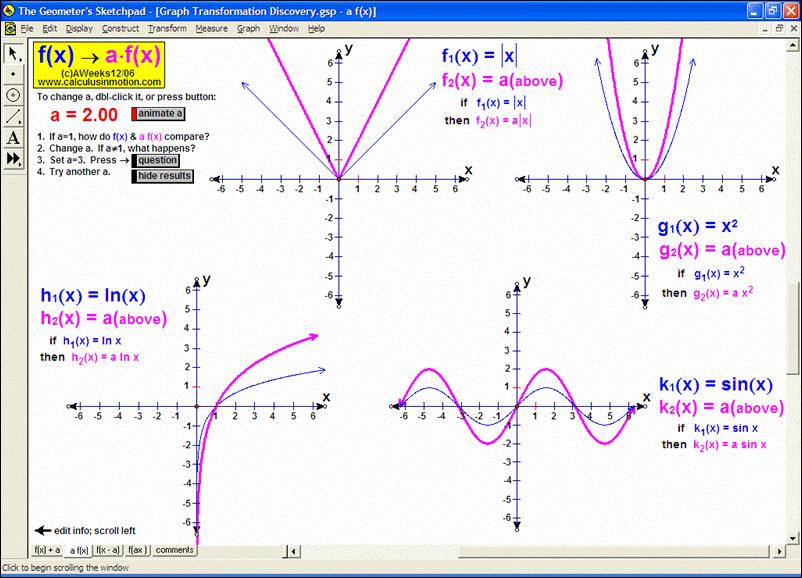
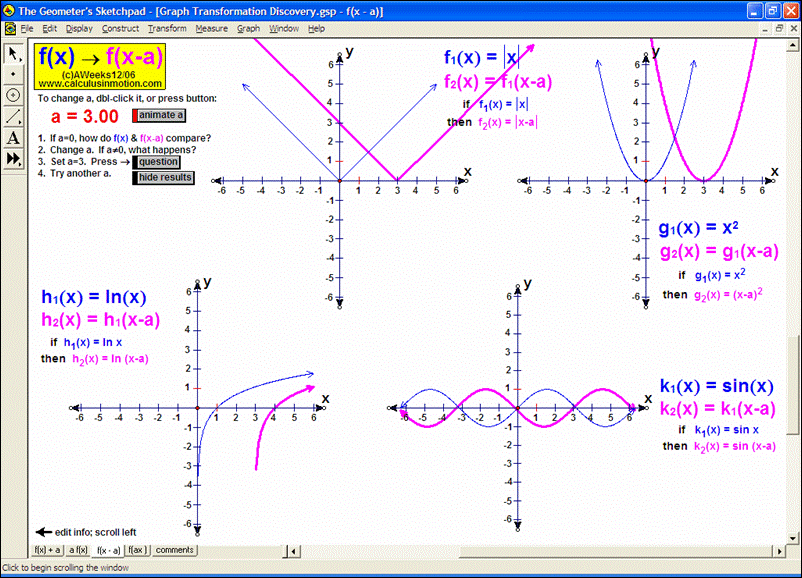
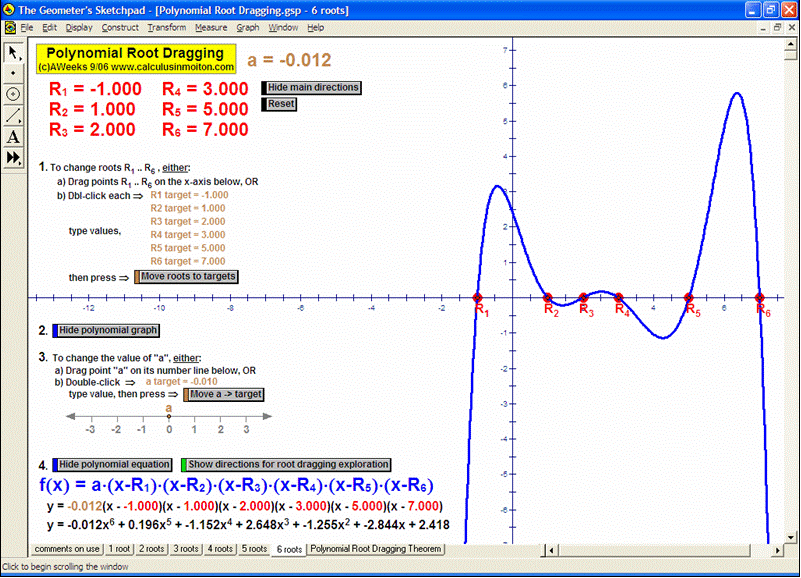
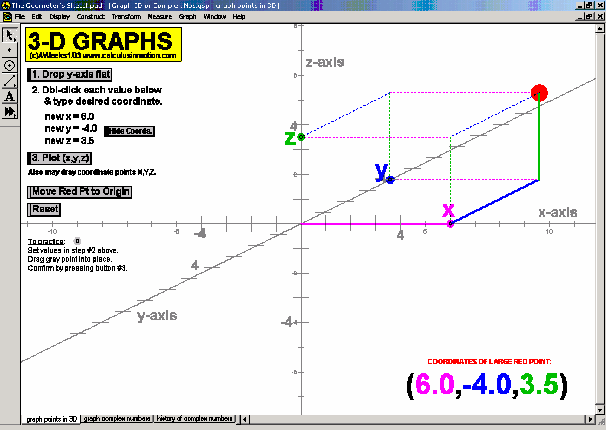
ADVANCED GRAPHING
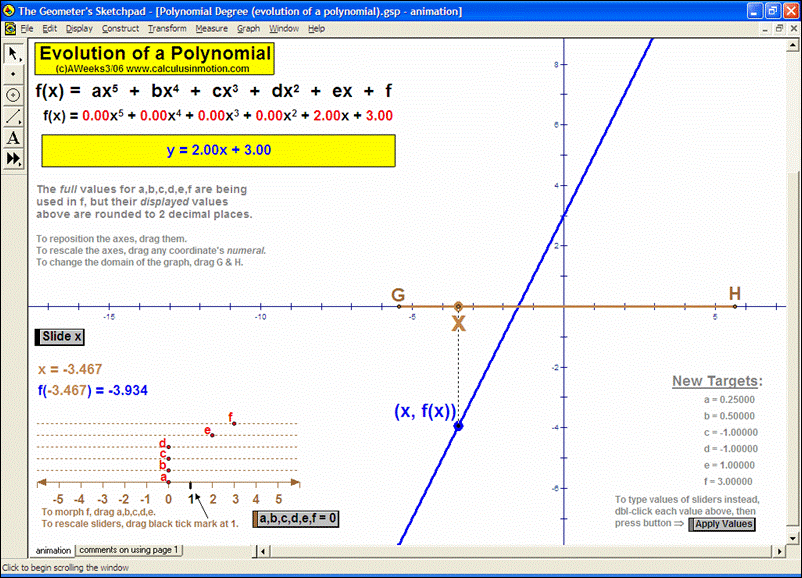
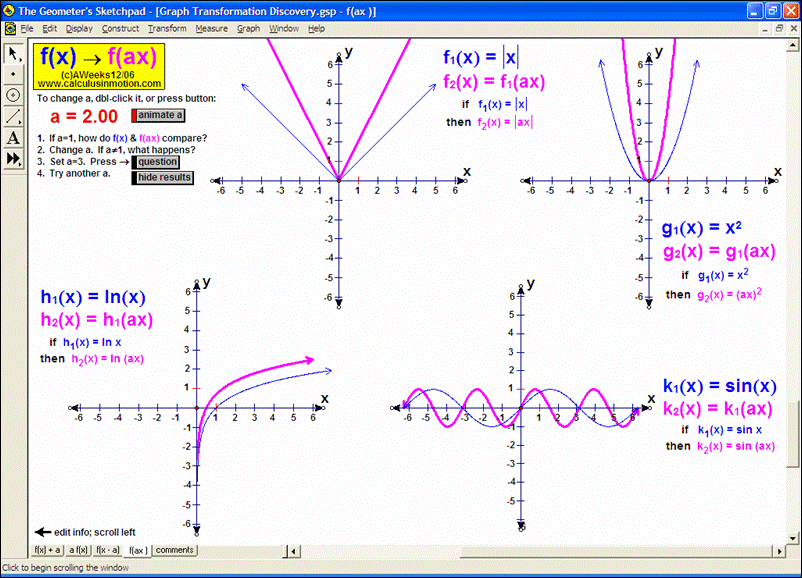
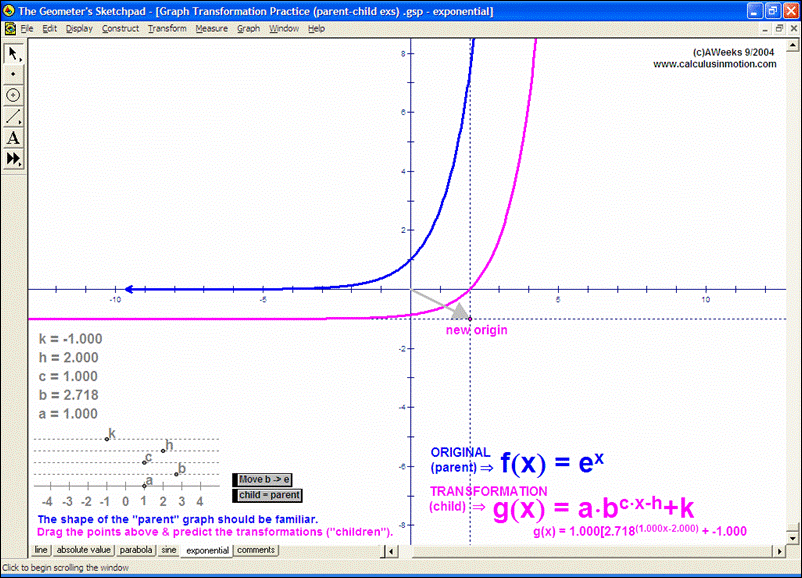
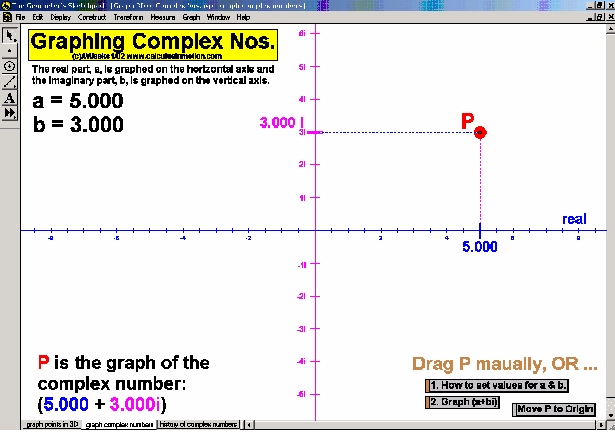
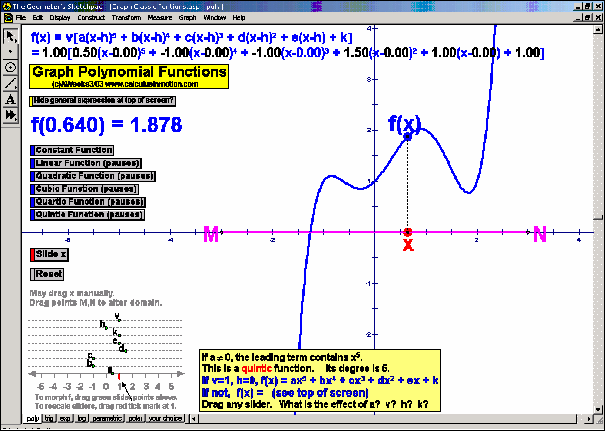
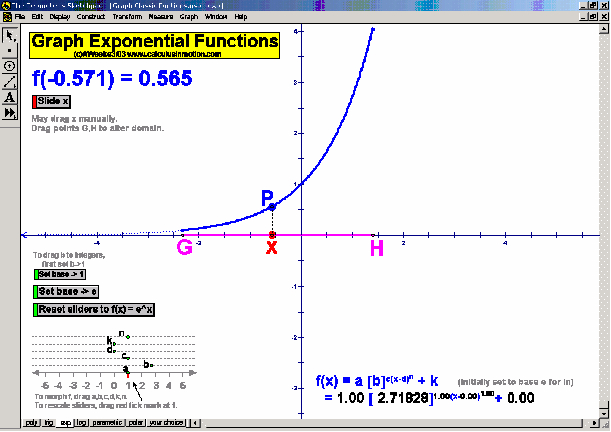
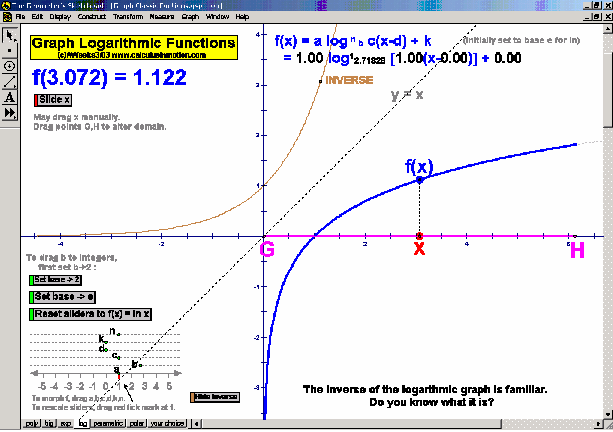
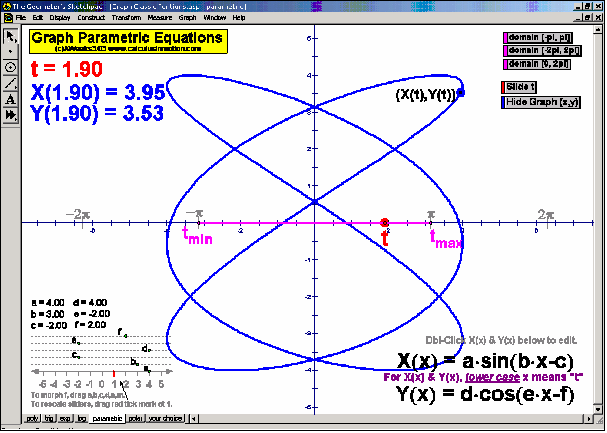
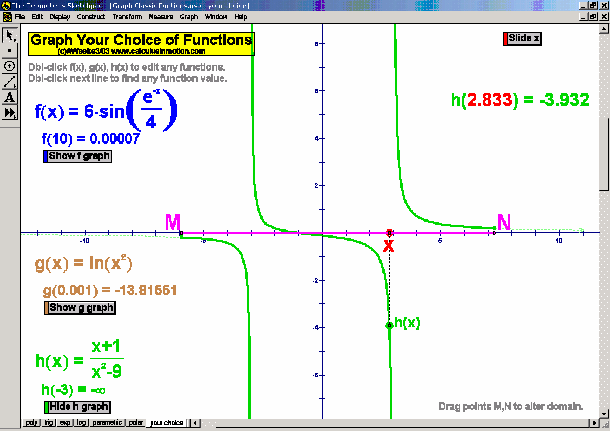
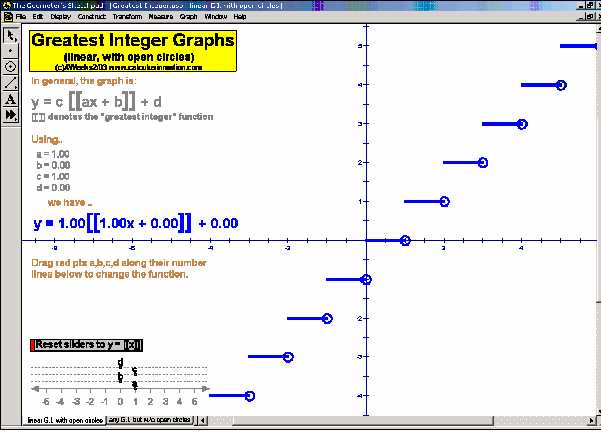
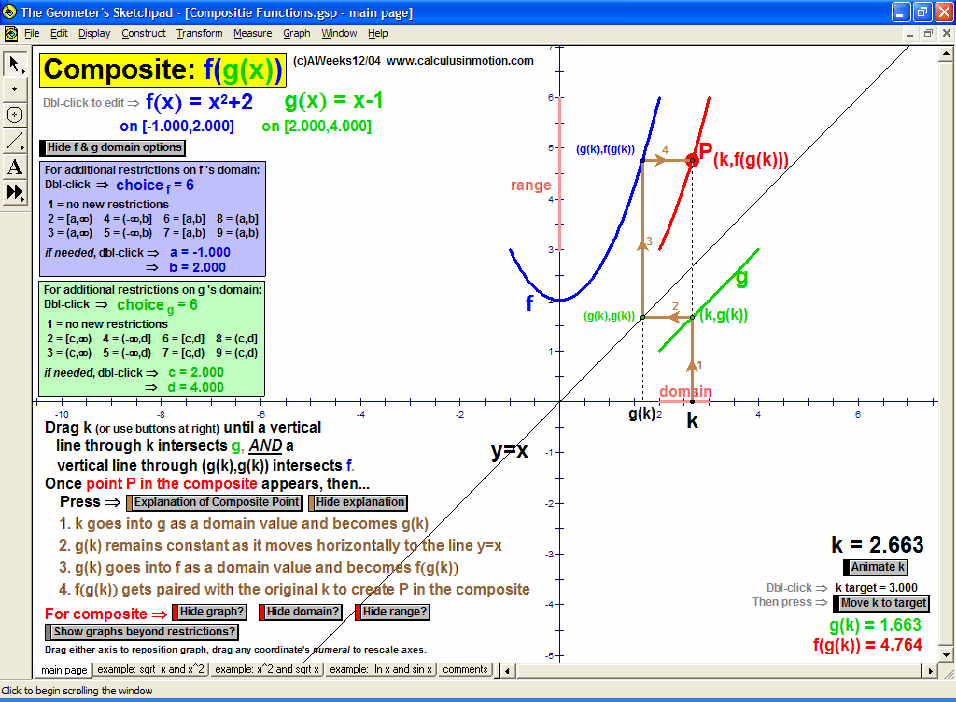
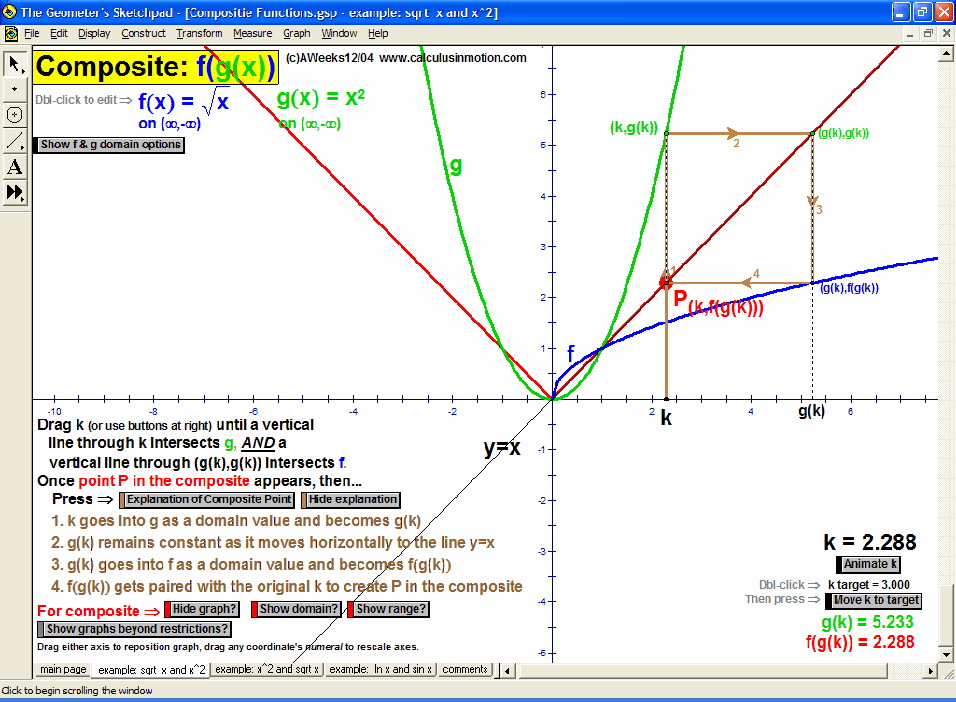
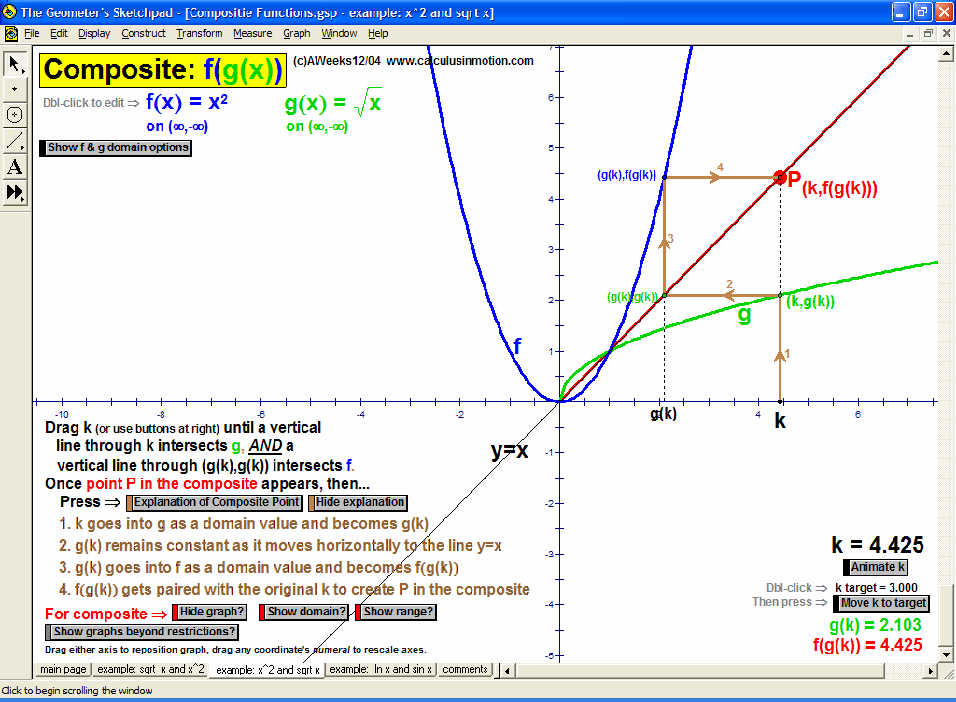
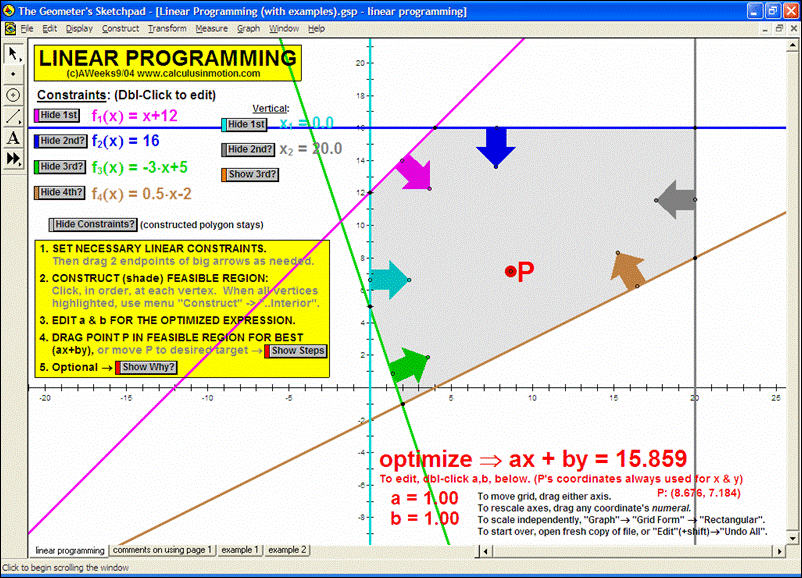
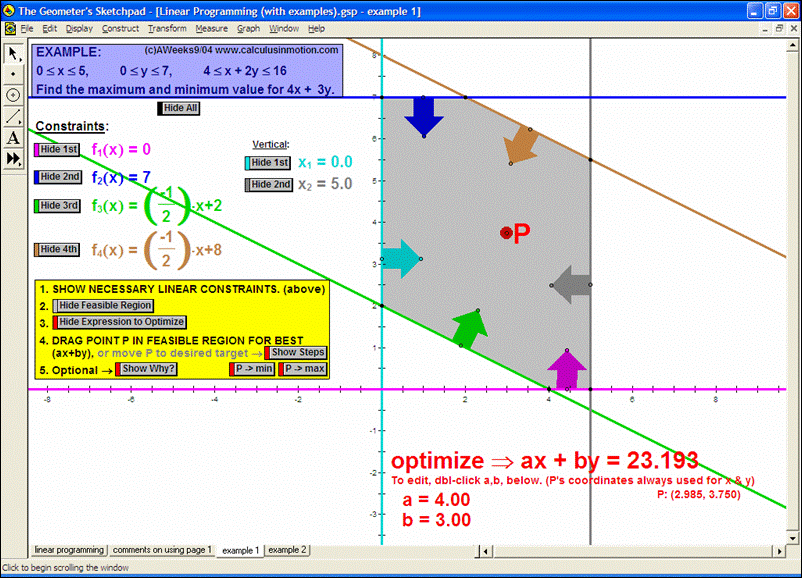
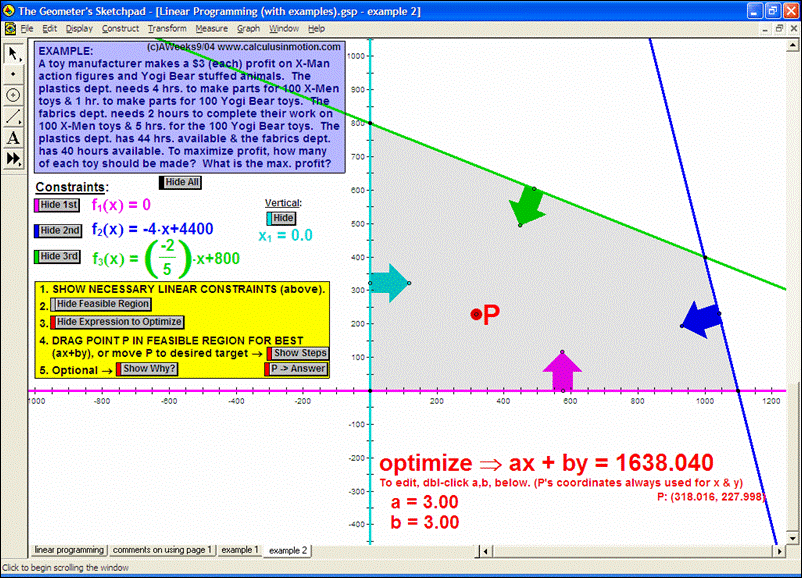
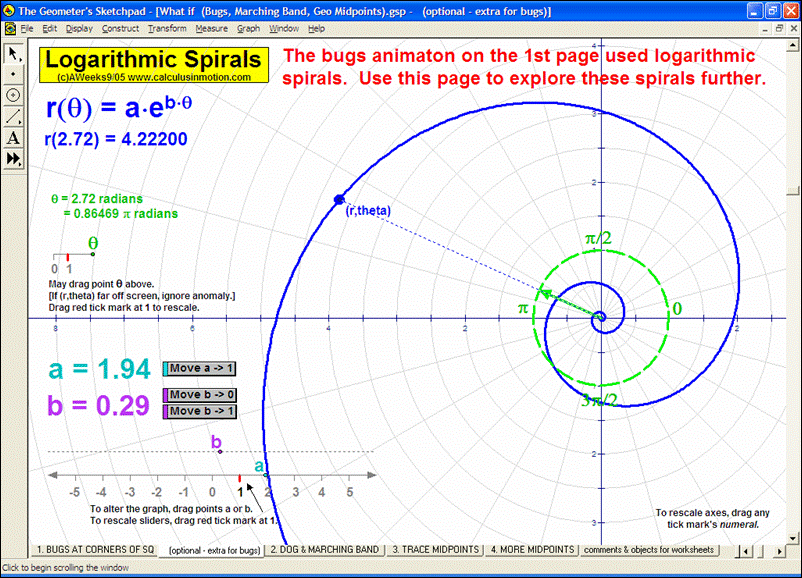
Dynamically graph points in 3D space or on the complex number plane (history included). Control coefficients of a polynomial to “morph” it from a constant function up through a 5th degree polynomial. Similarly “morph” graphs of logarithmic & exponential functions, parametric & polar graphs, greatest integer functions, and inverses. Explore how composites of functions are created, and create linear programming examples.
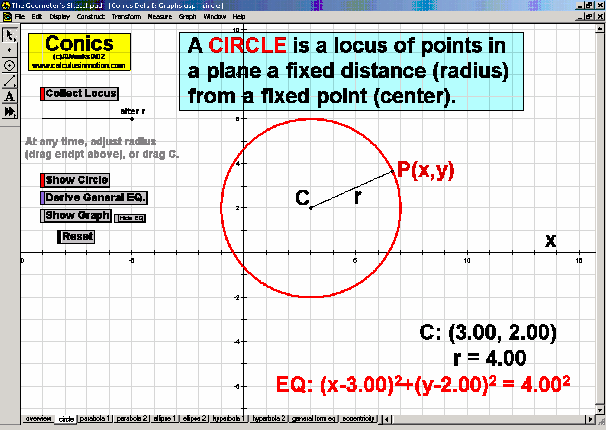
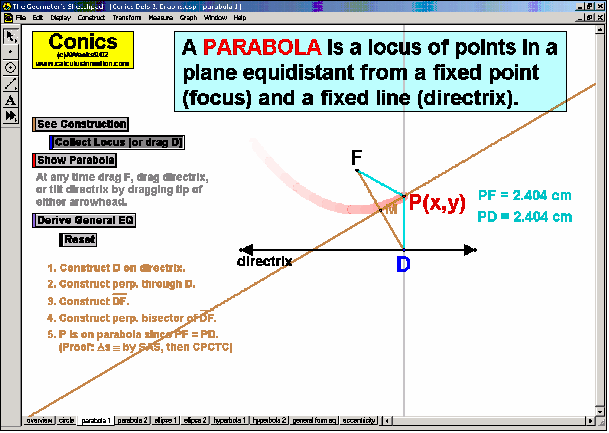
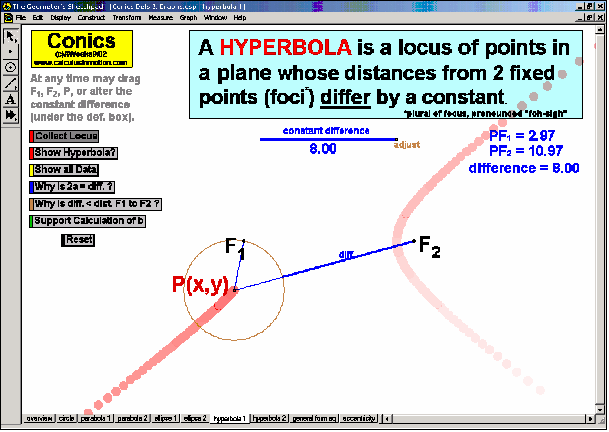
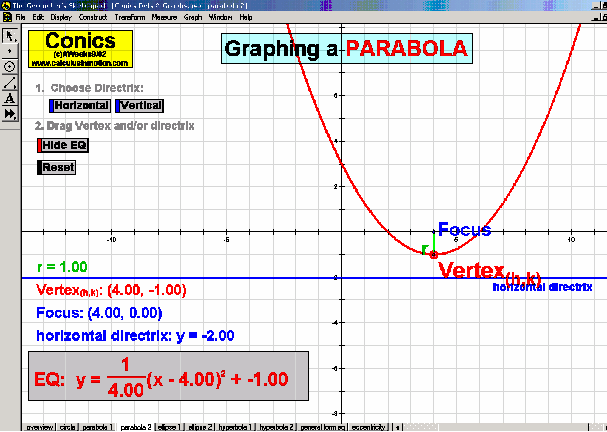
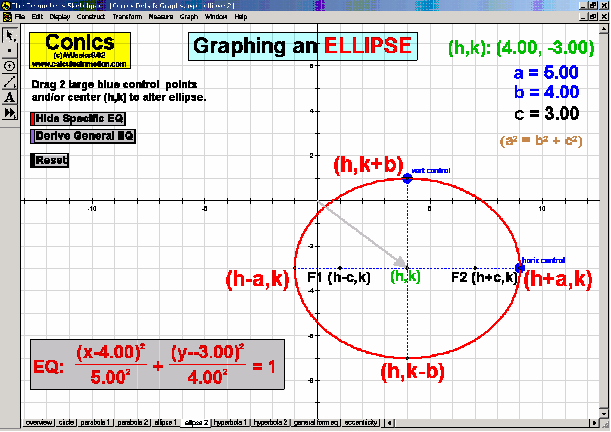
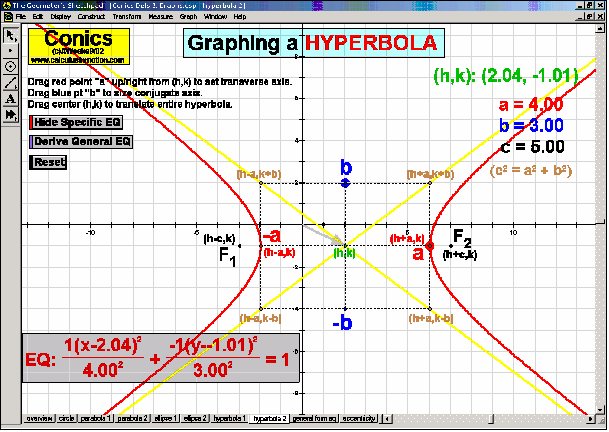
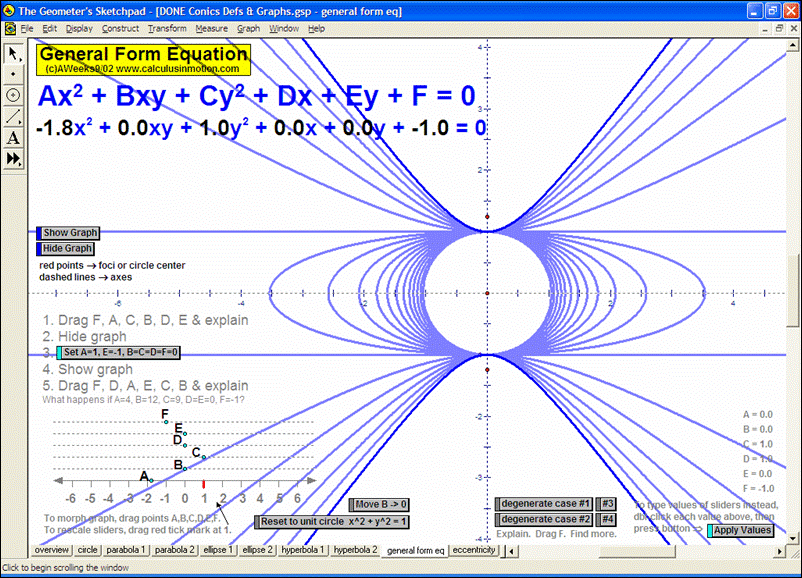
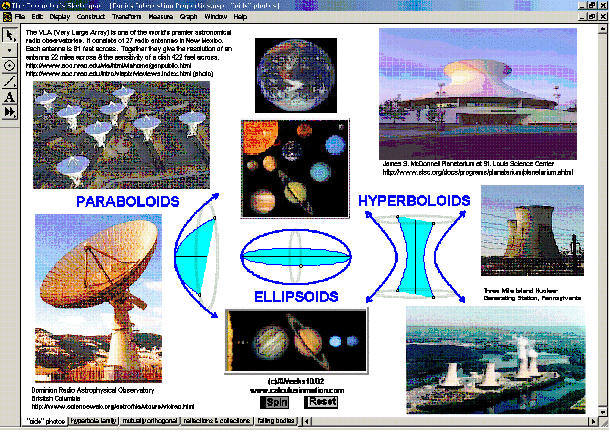
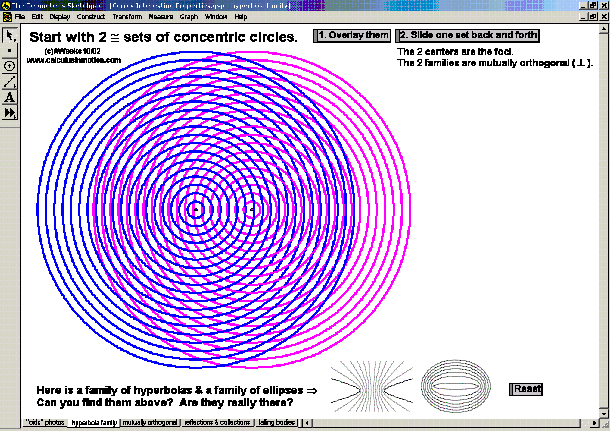
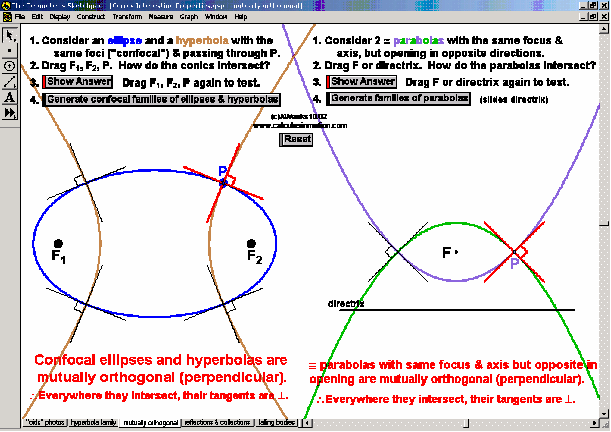
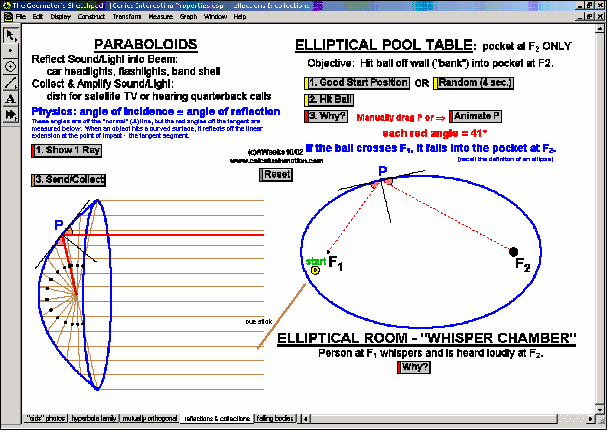
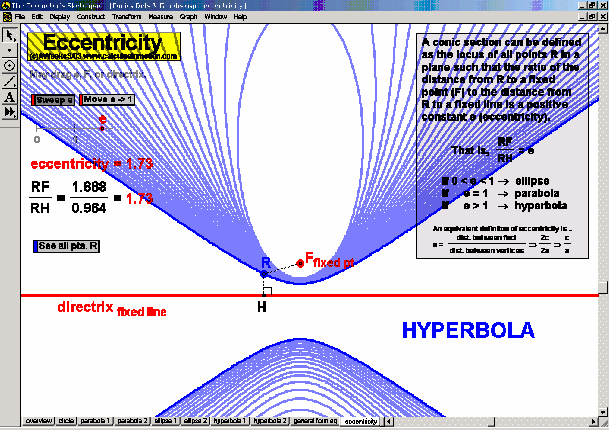
CONICS & THEIR APPLICATIONS
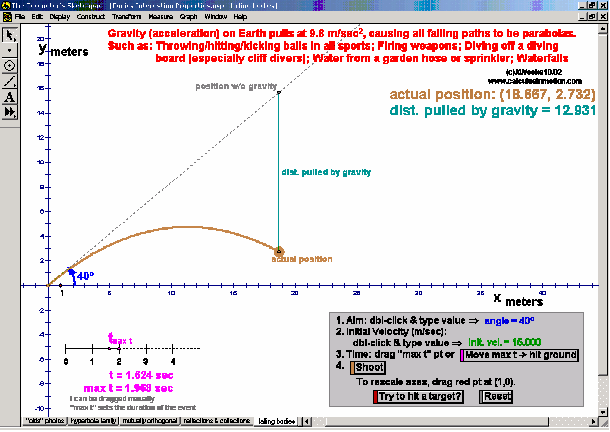
Dynamically create each conic section from its definition. Graph and “morph” all features of each. Alter coefficients of the general equation or eccentricity to “morph” one conic into another. Explore applications to satellite dishes, elliptical pool tables, whisper chambers, & falling objects.
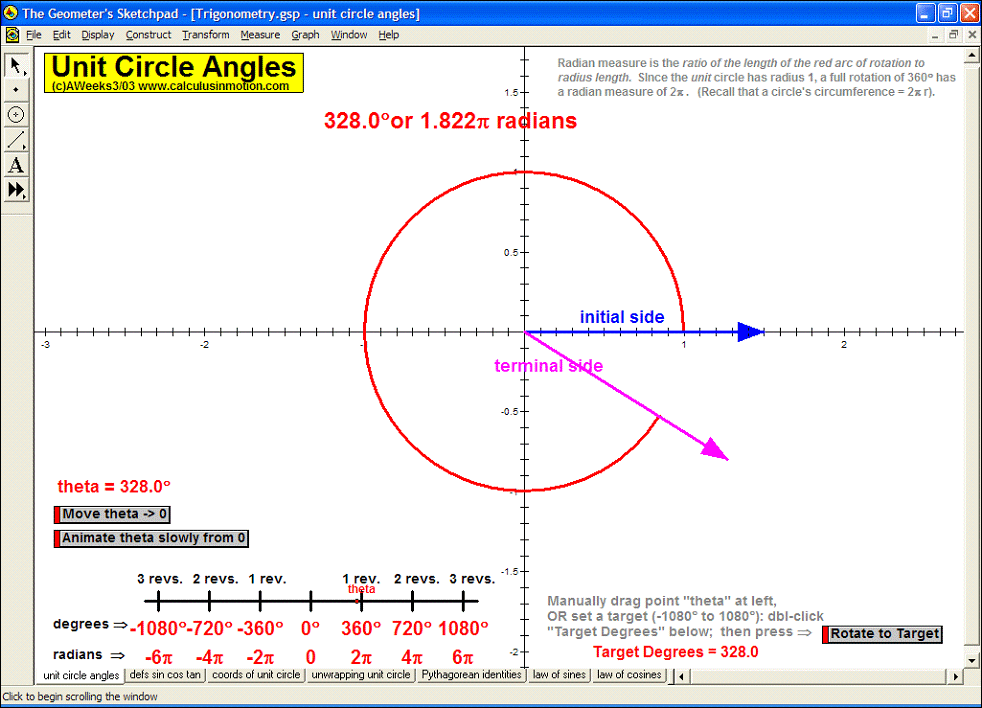
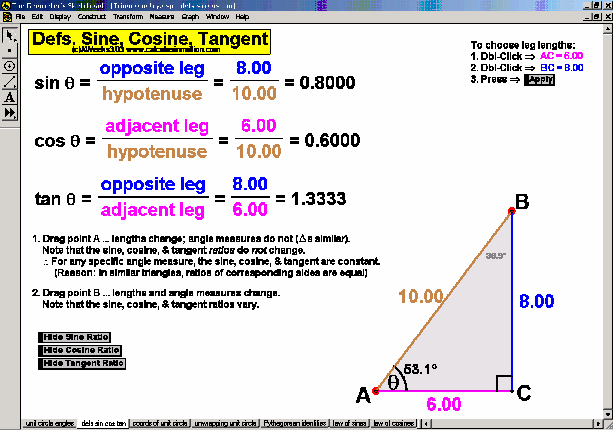
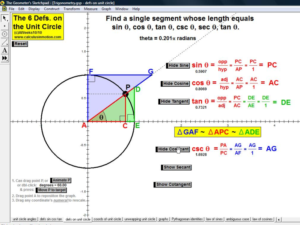
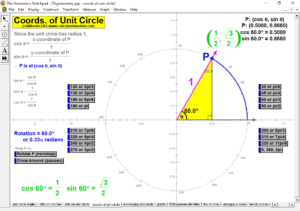
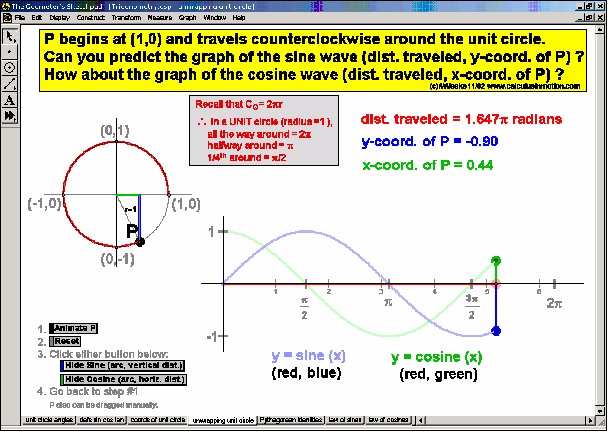
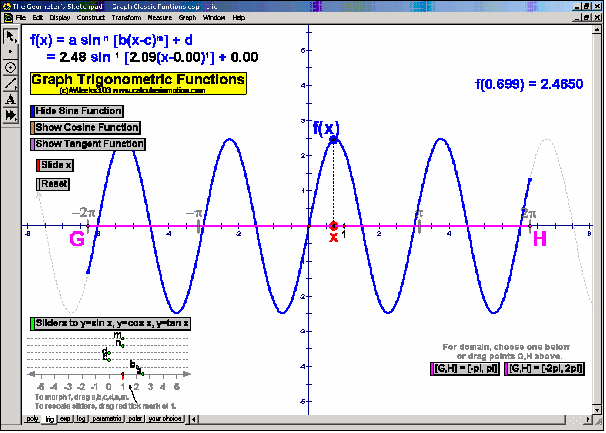
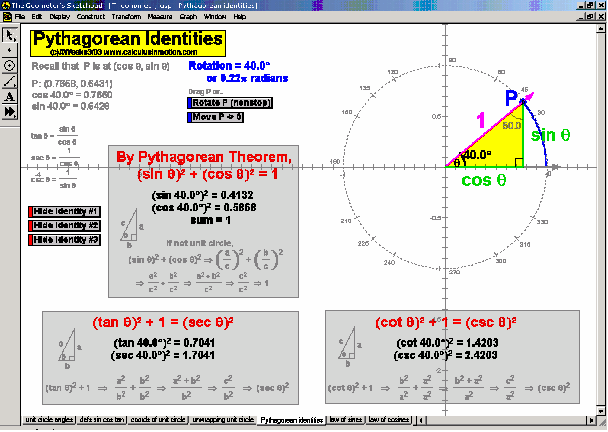
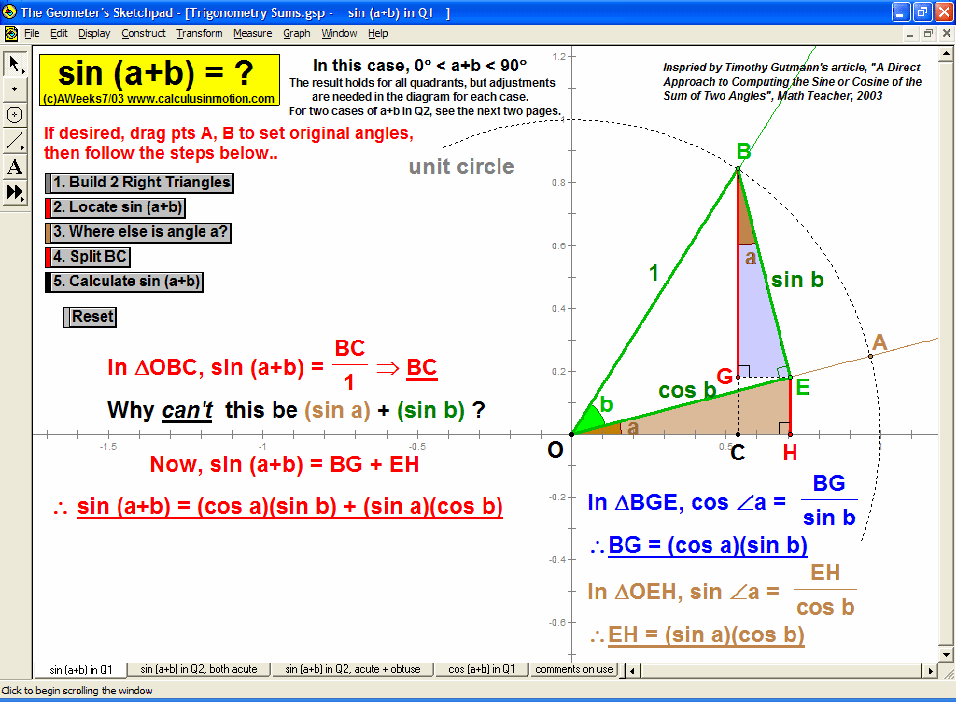
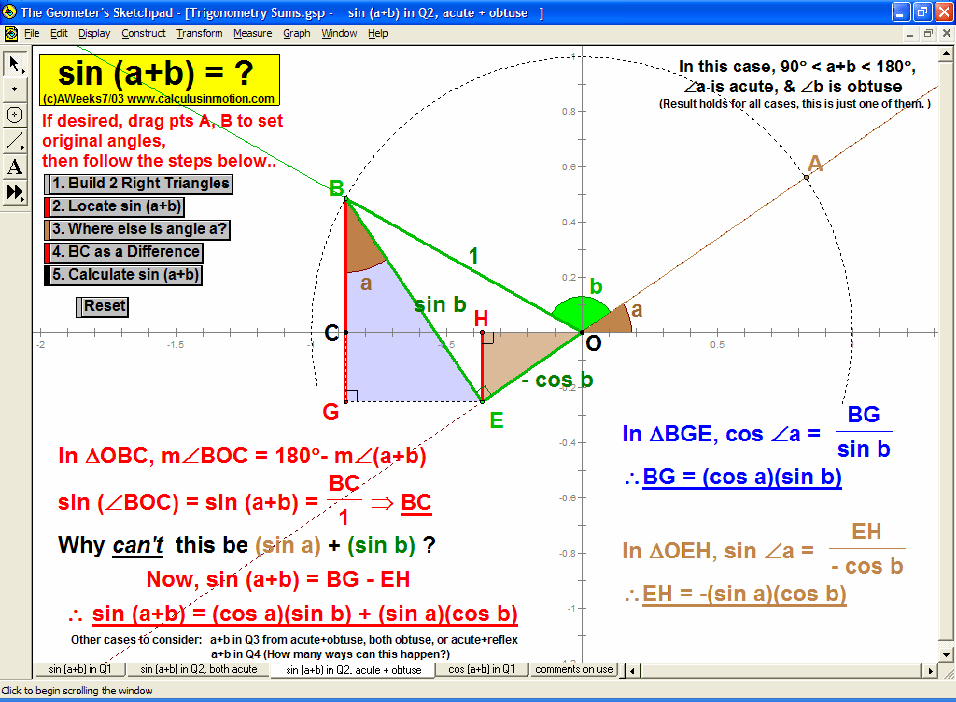
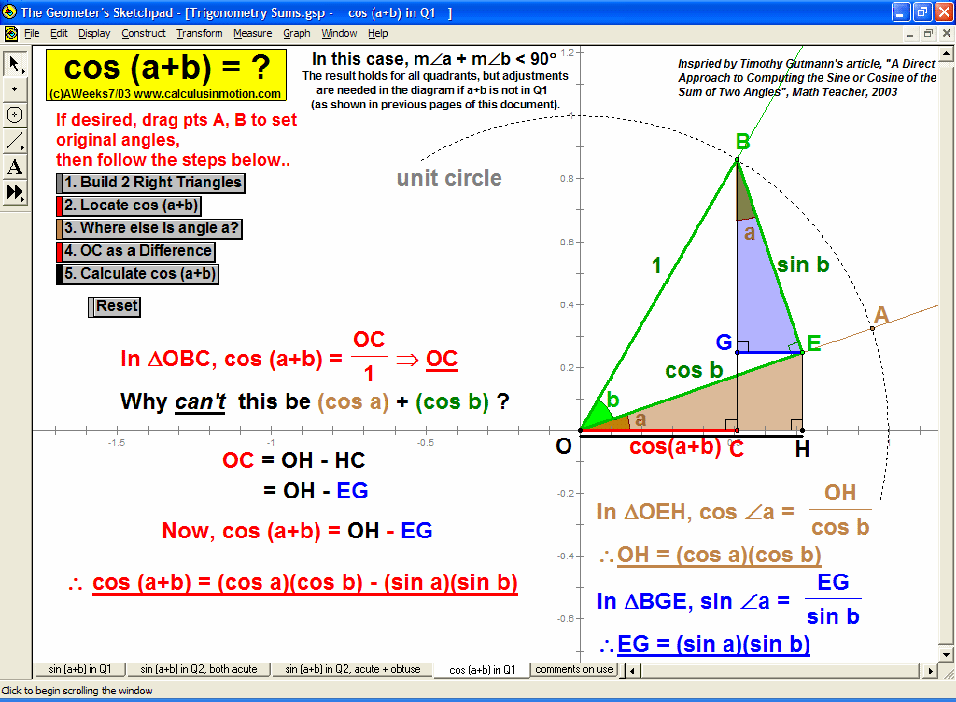
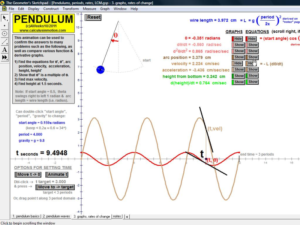
TRIGONOMETRY
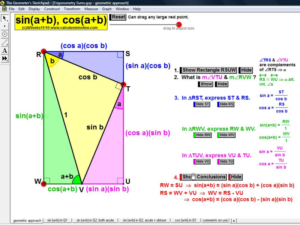
In an environment where rotation is real, not merely imagined, thoroughly investigate the unit circle’s angles, coordinates, and ratios. Literally unwrap the unit circle to form sine and cosine waves. Dilate and translate trigonometric graphs to explore amplitude, period, and shift. Explore and prove Pythagorean identities, the Law of Sines, and the Law of Cosines. Convincingly demonstrate that sin (a+b) can’t be (sin a + sin b).
THEOREMS
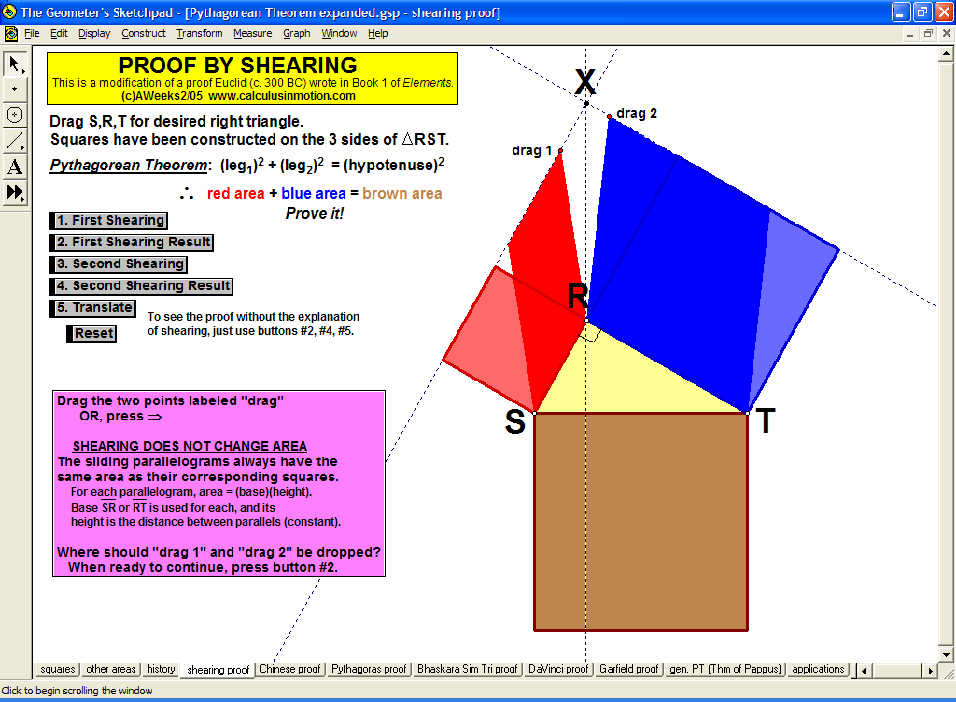
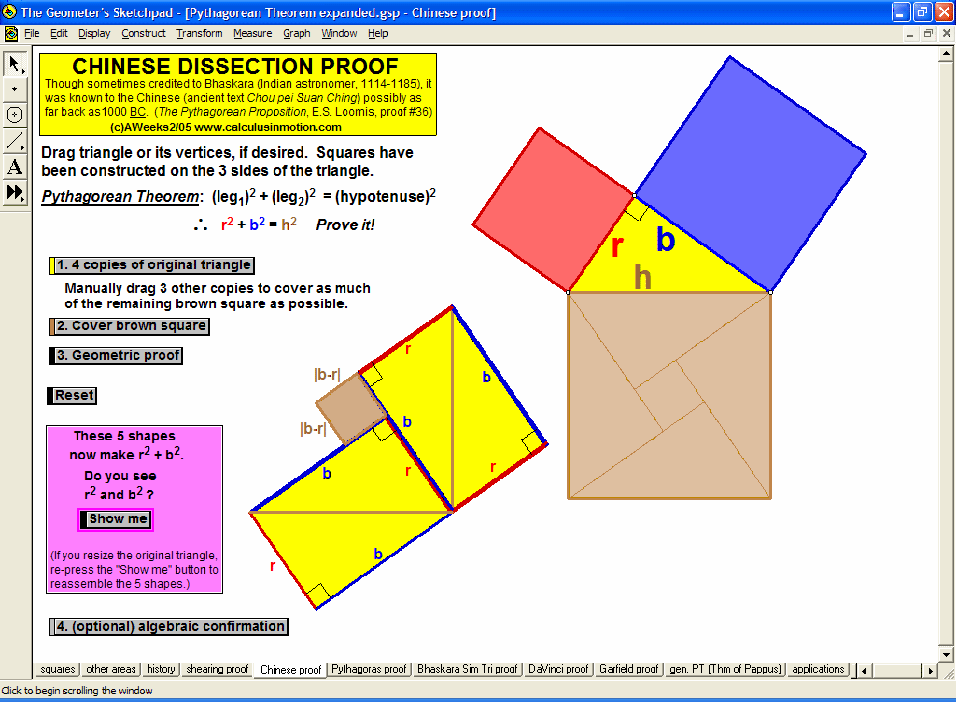
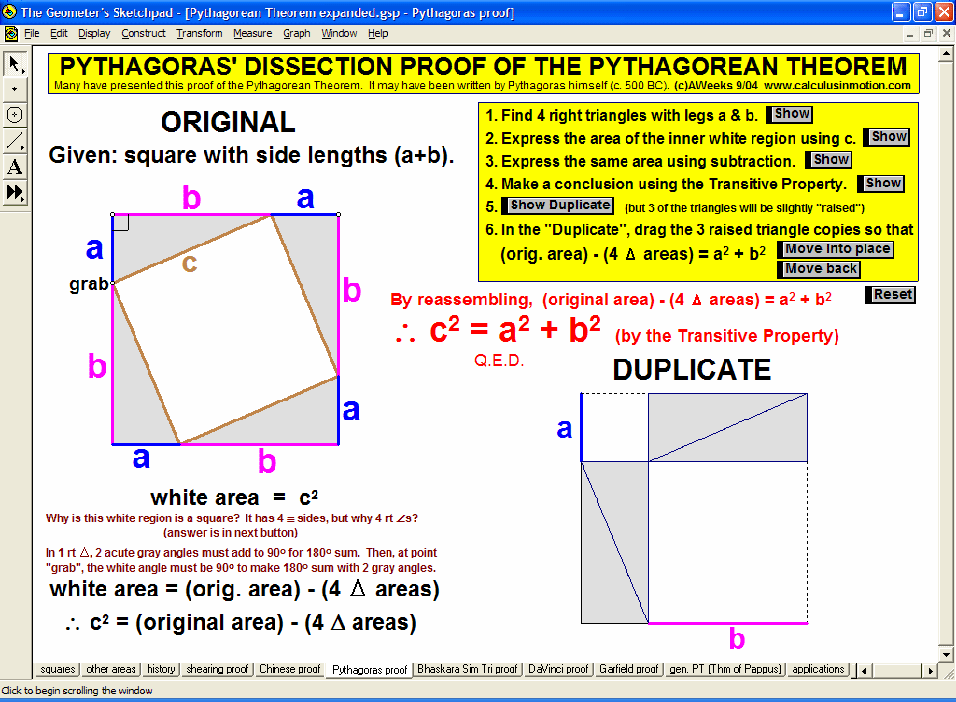
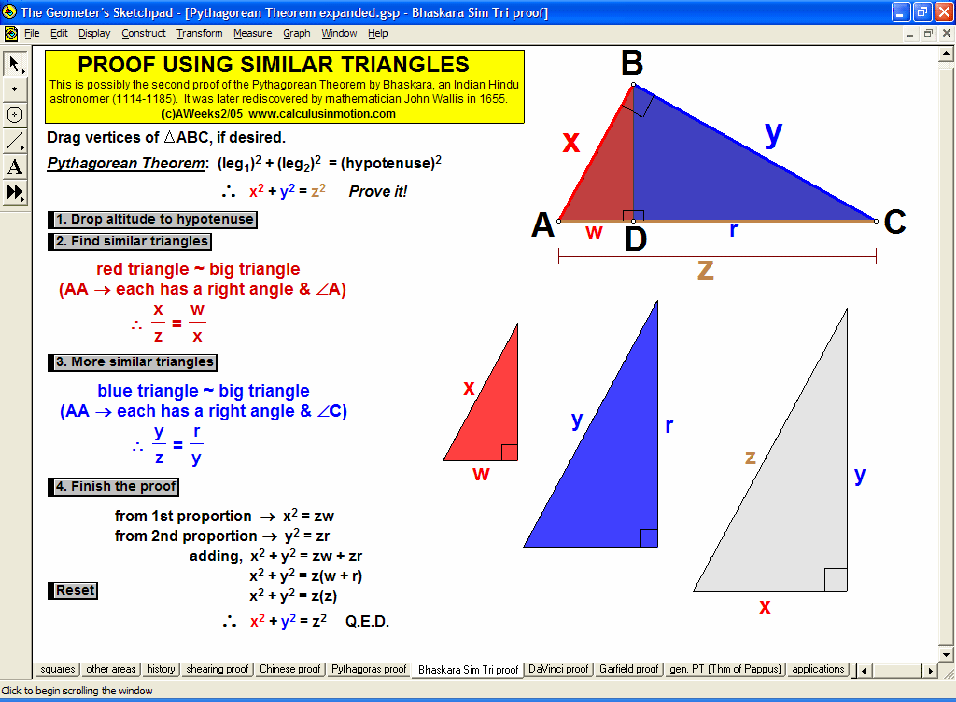
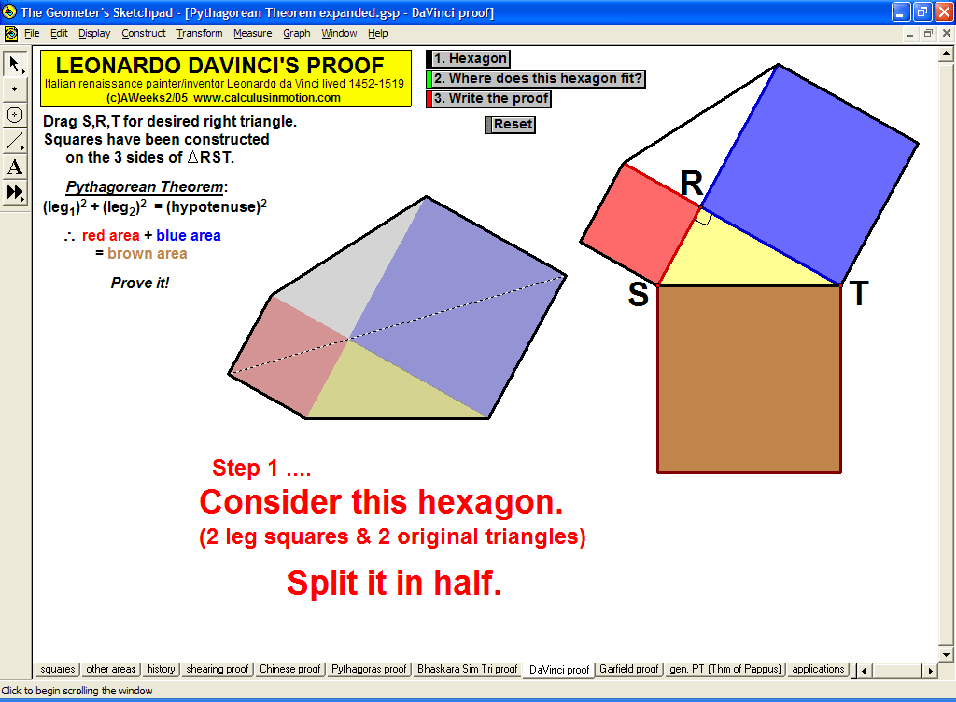
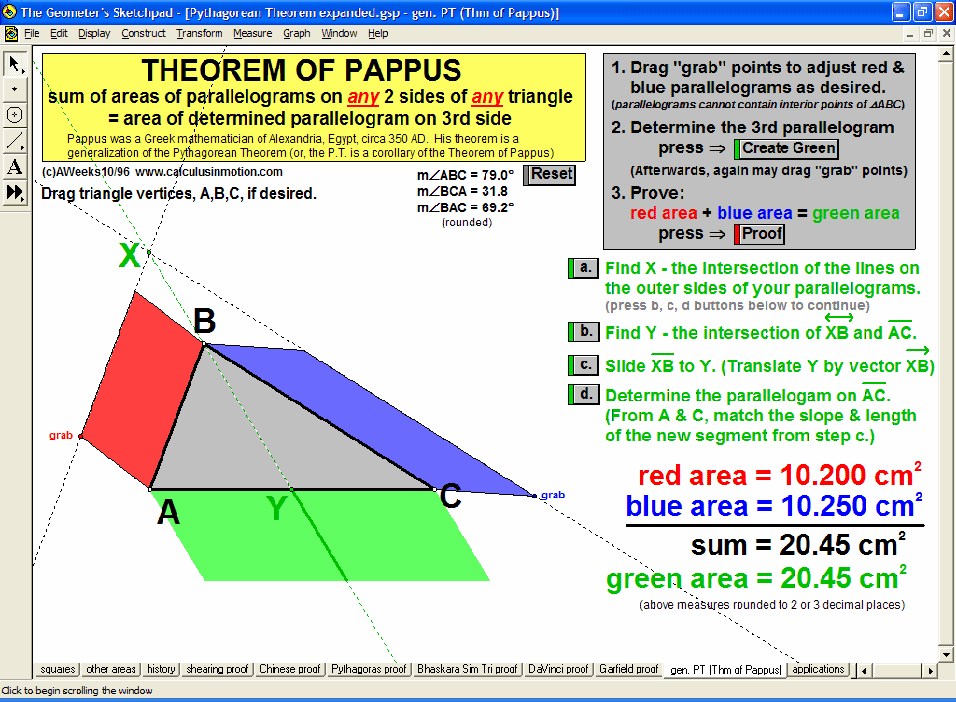
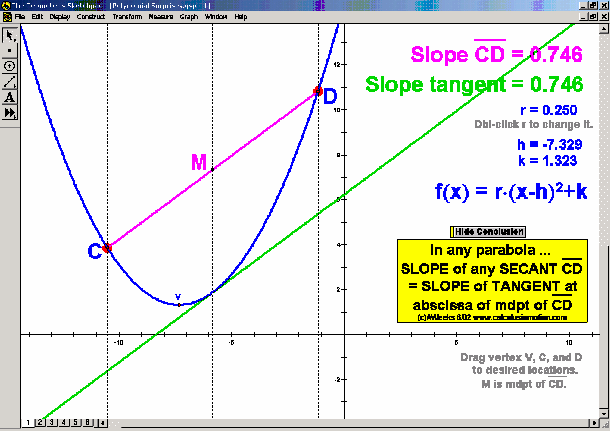
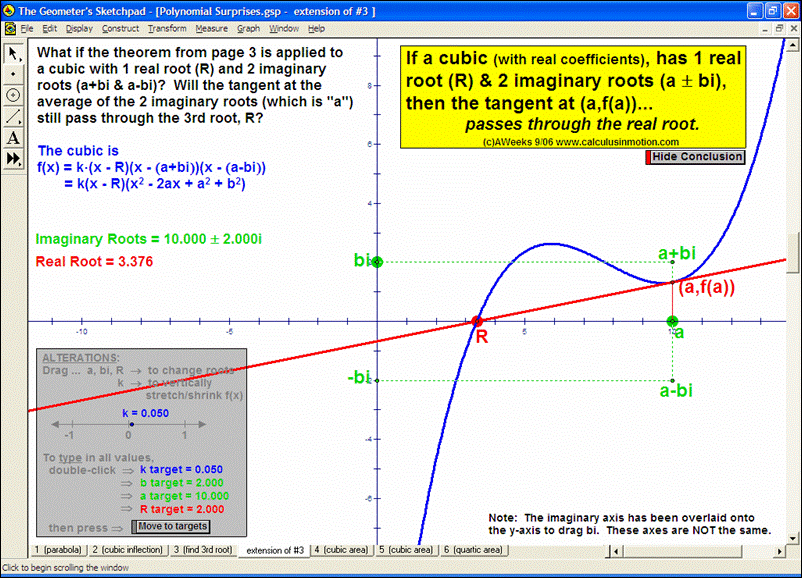
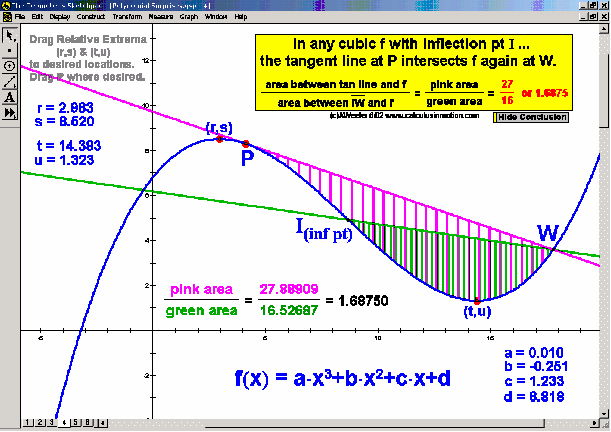
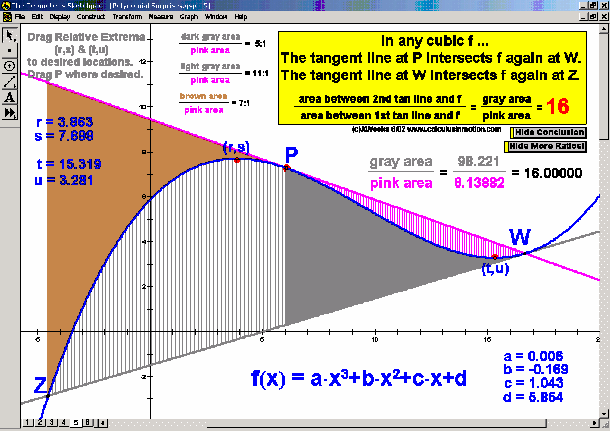
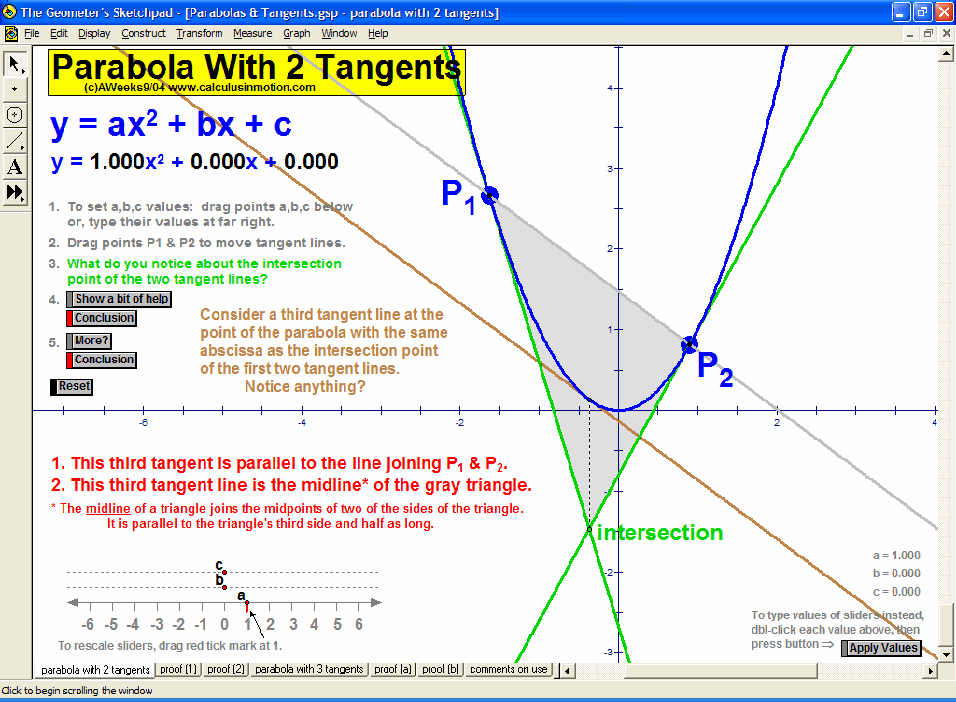
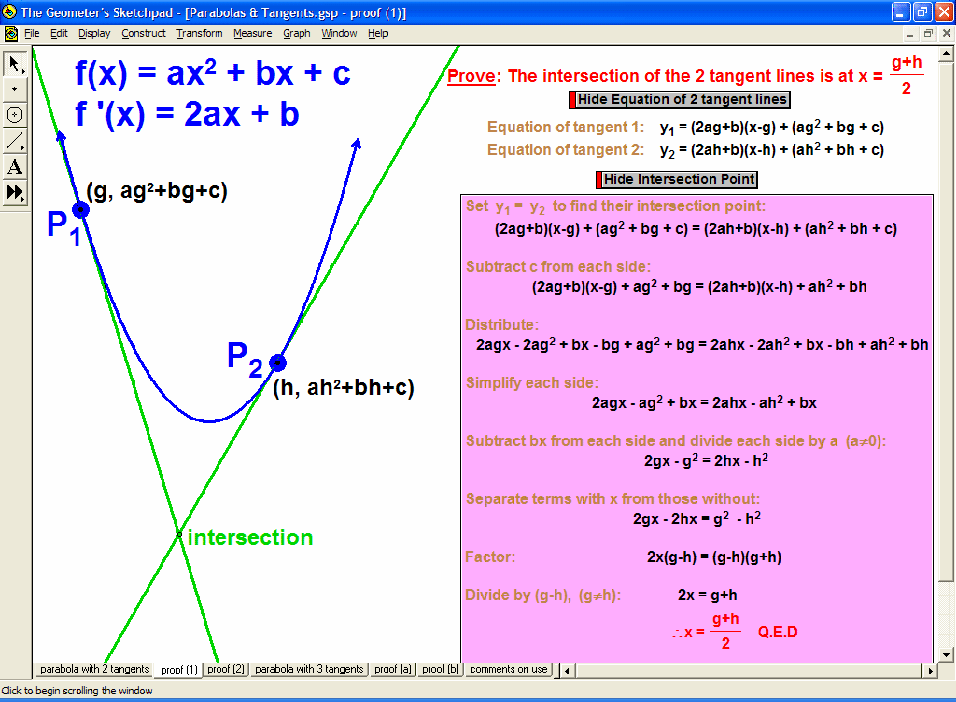
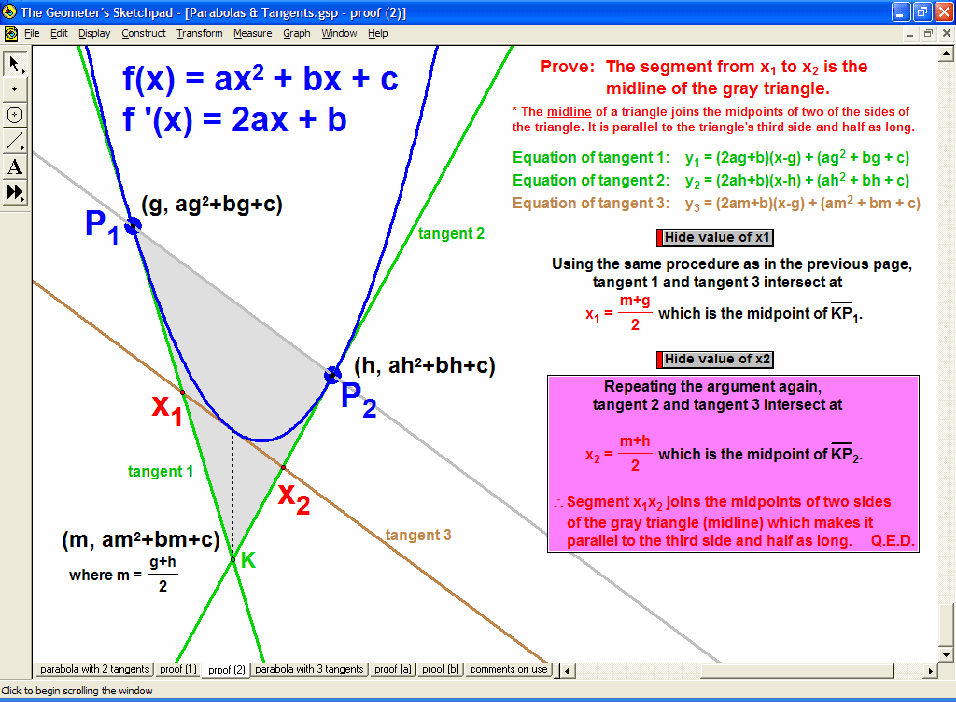
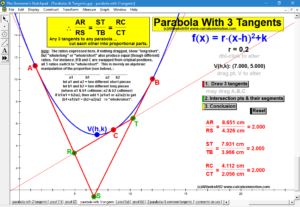
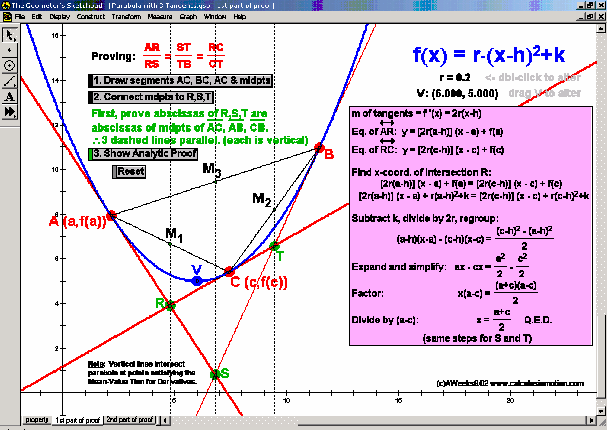
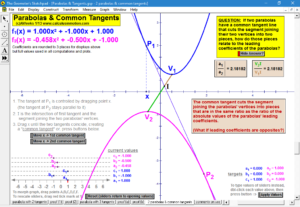
Dynamically explore conventional theorems such as the Pythagorean Theorem (+ history) along with 7 different visual proofs of it. In addition, discover a large selection of unusual and unexpected theorems concerning tangents to parabolas, cubics, and quartics that will amaze and fascinate your students while laying an excellent foundation for more advanced mathematical study.
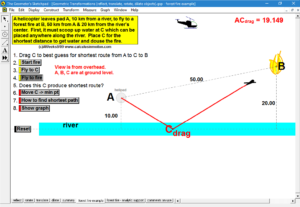
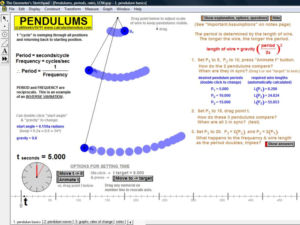
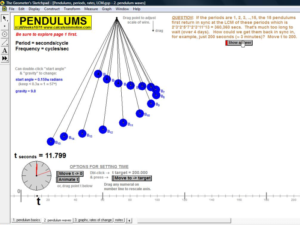
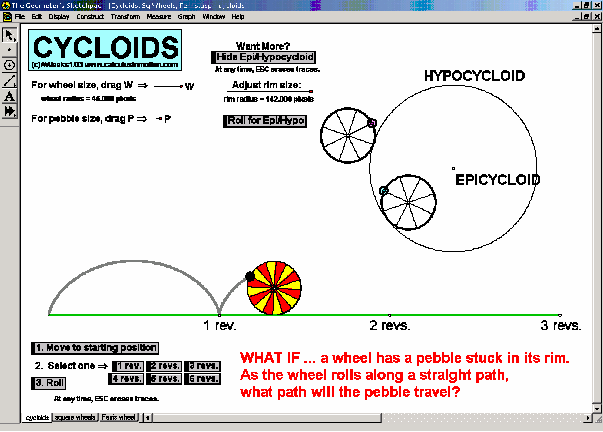
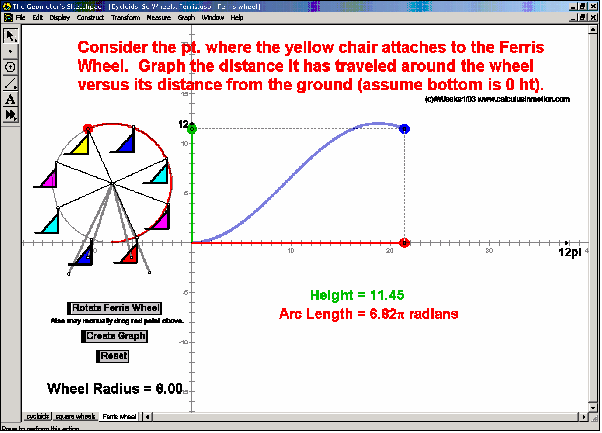
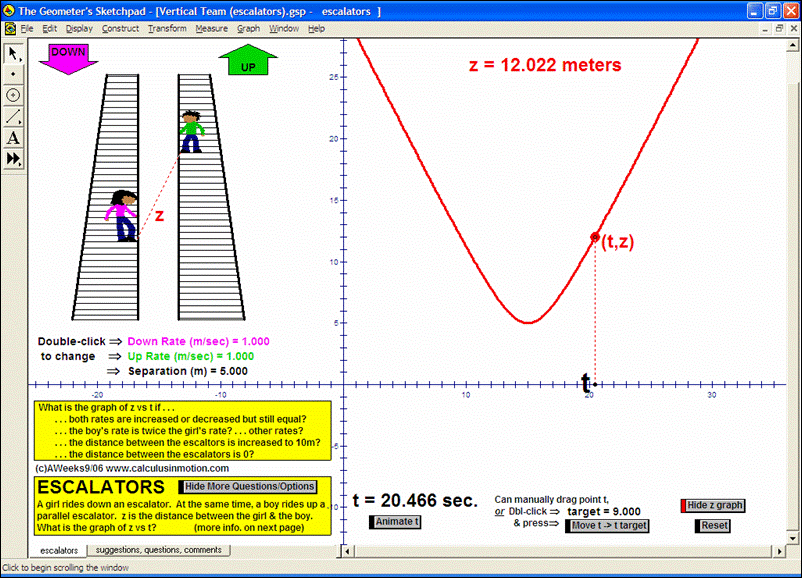
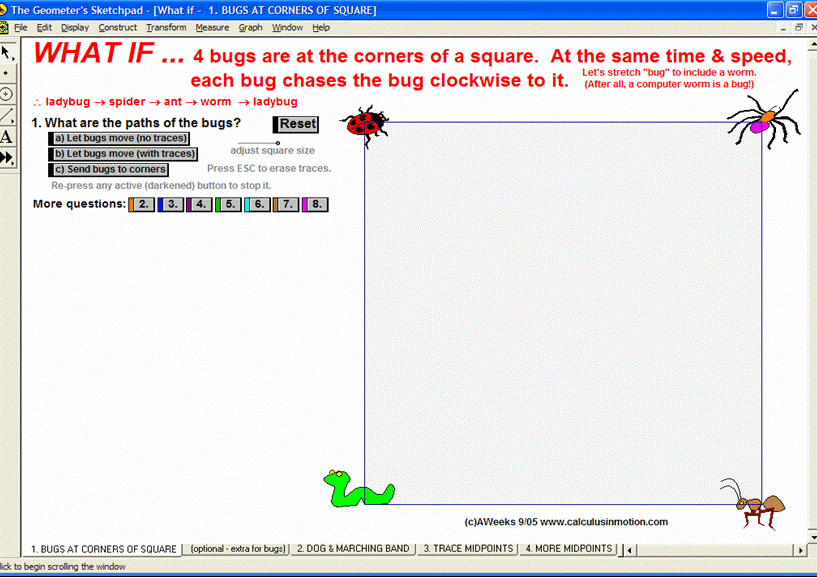
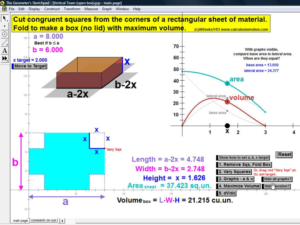
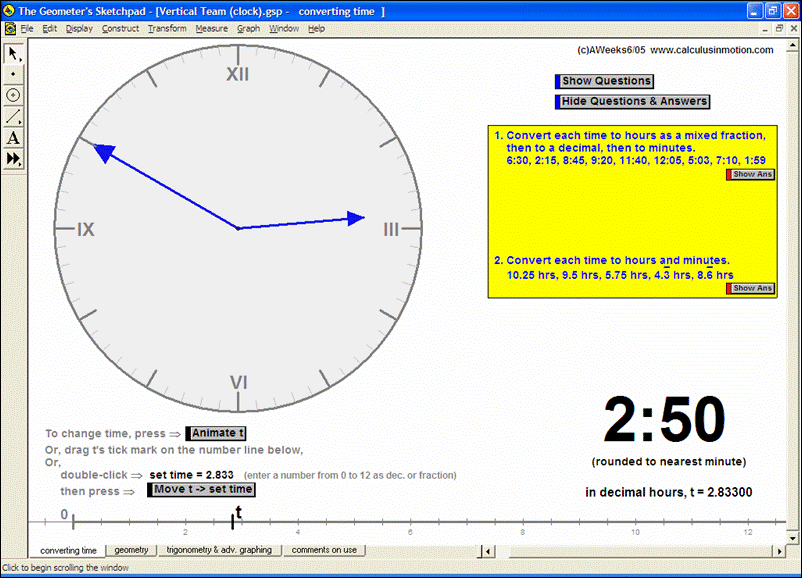
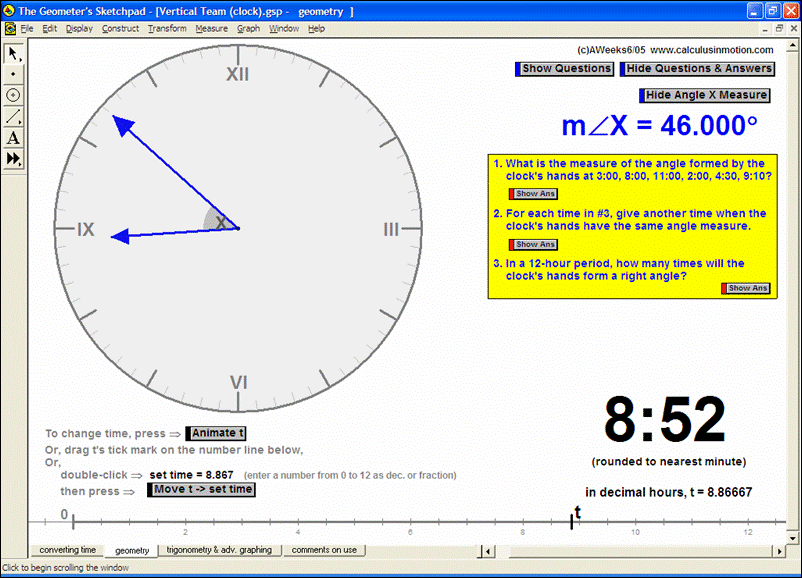
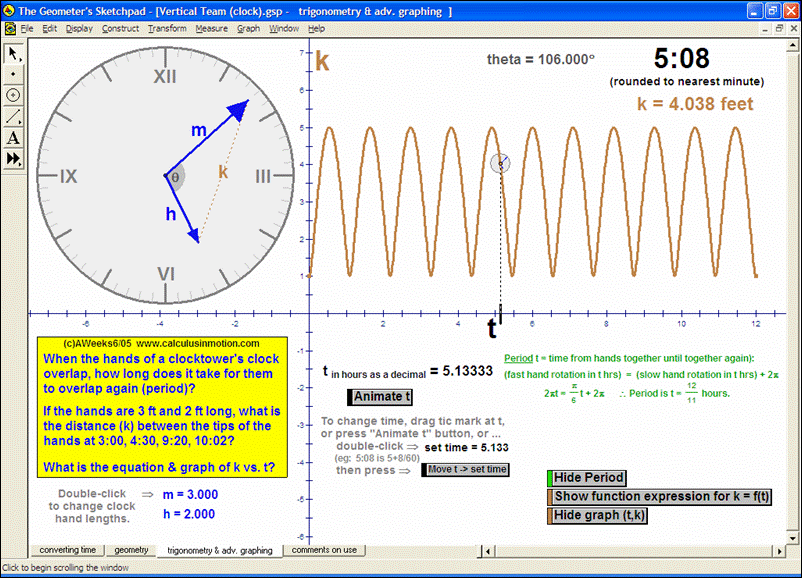
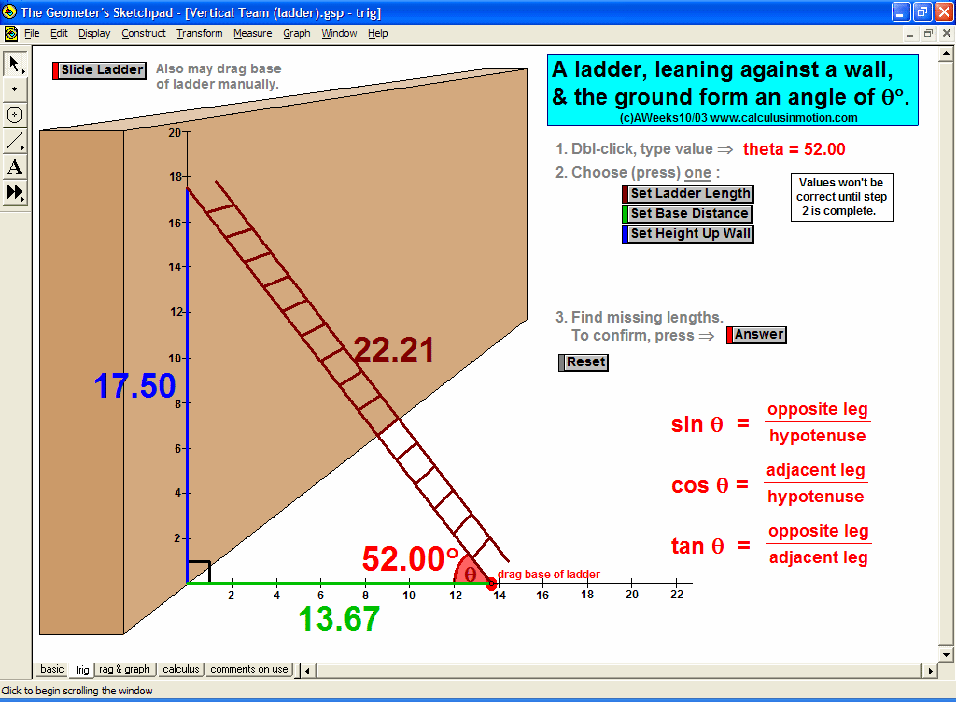
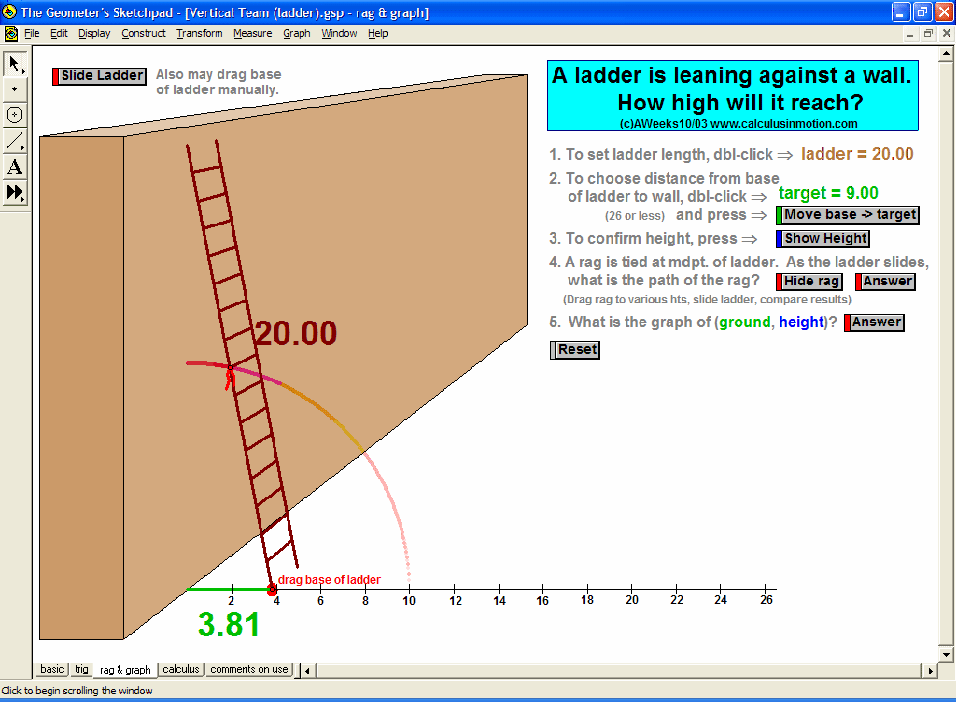
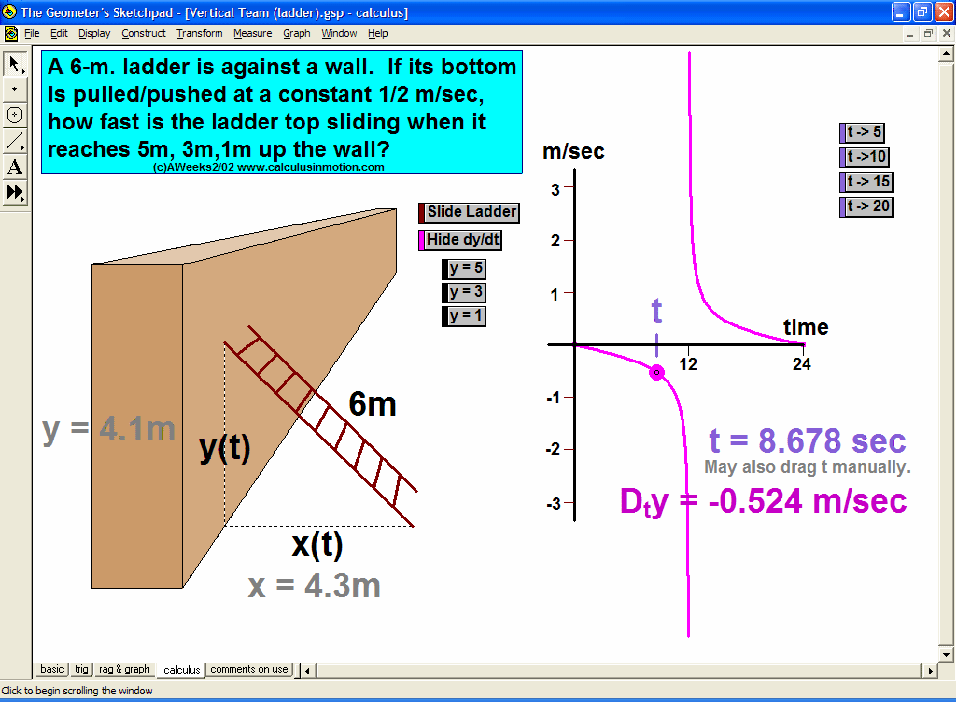
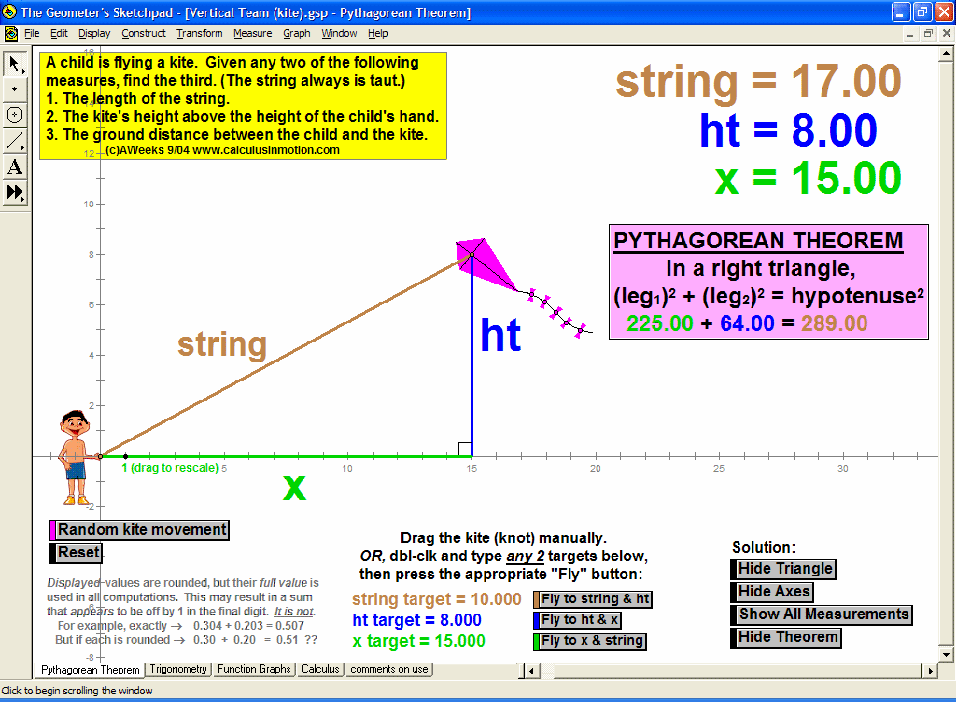
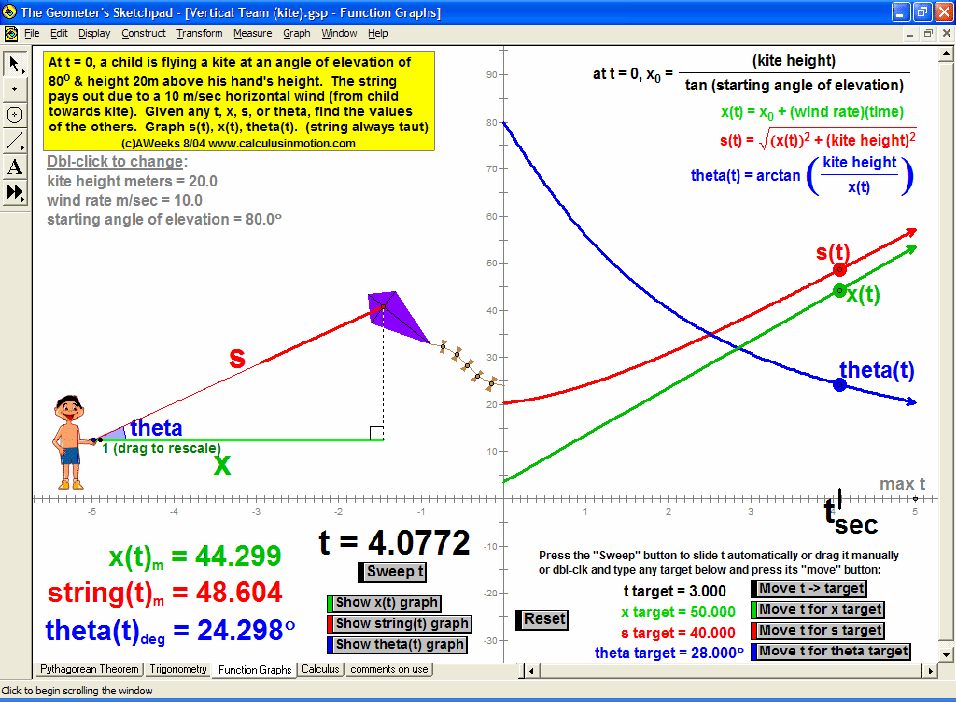
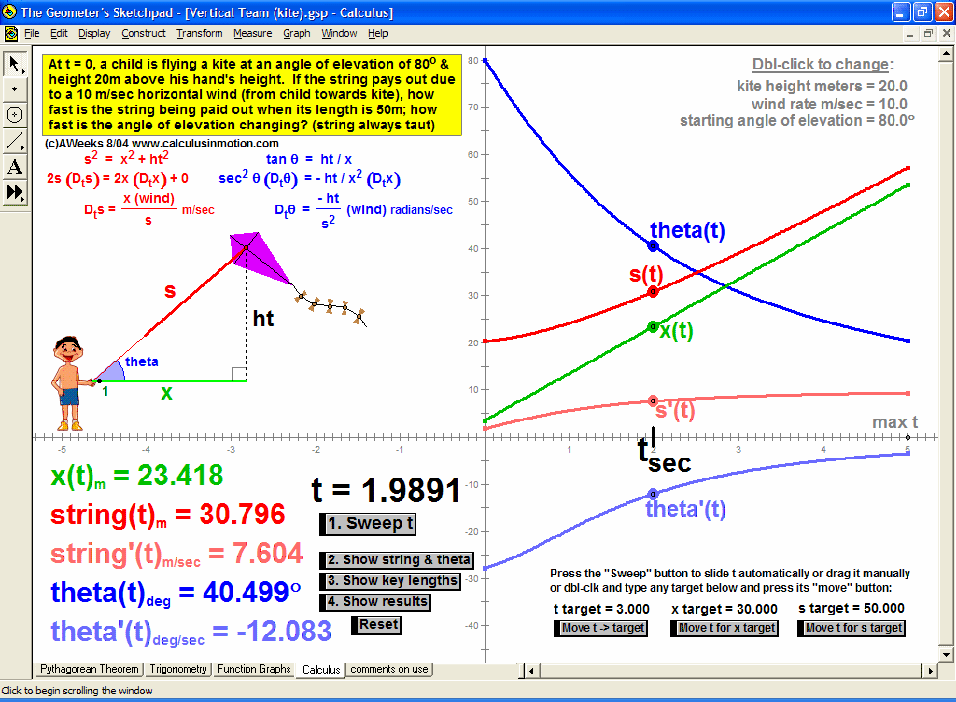
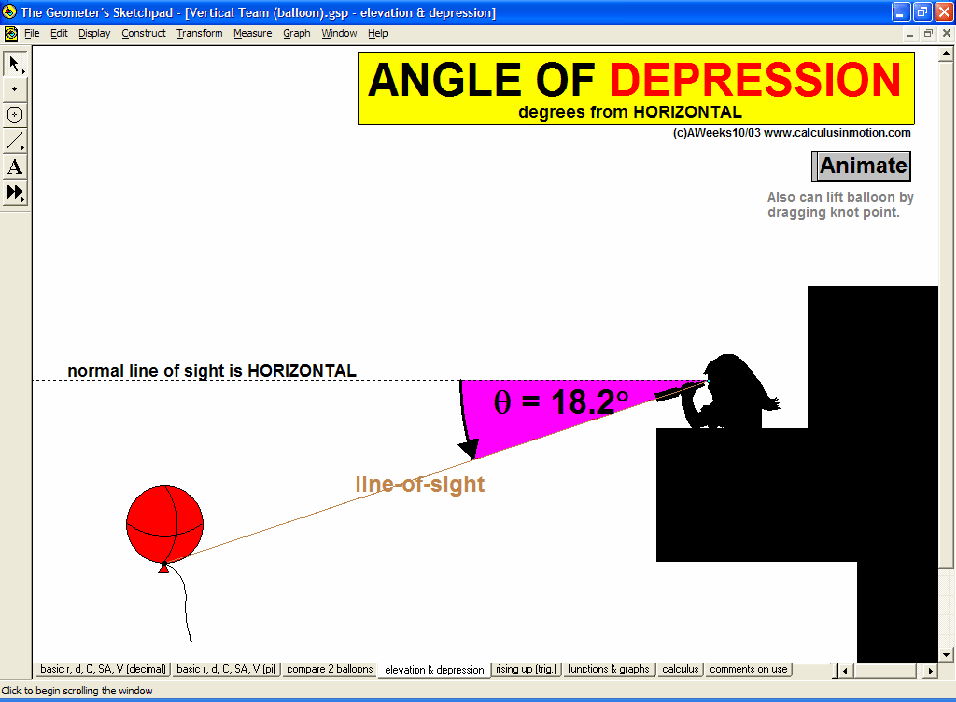
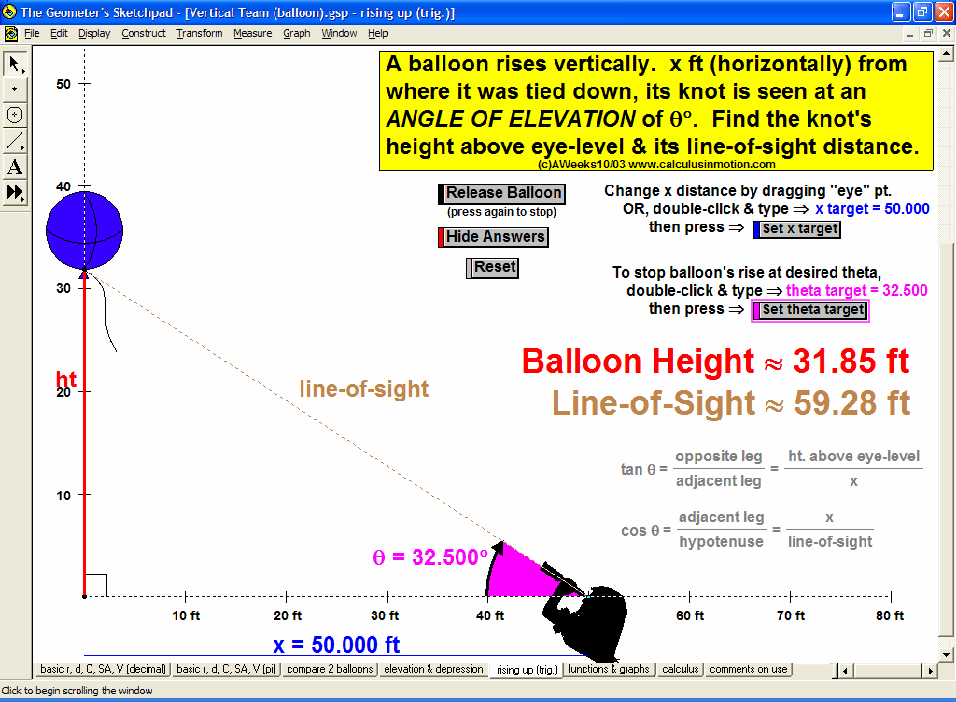
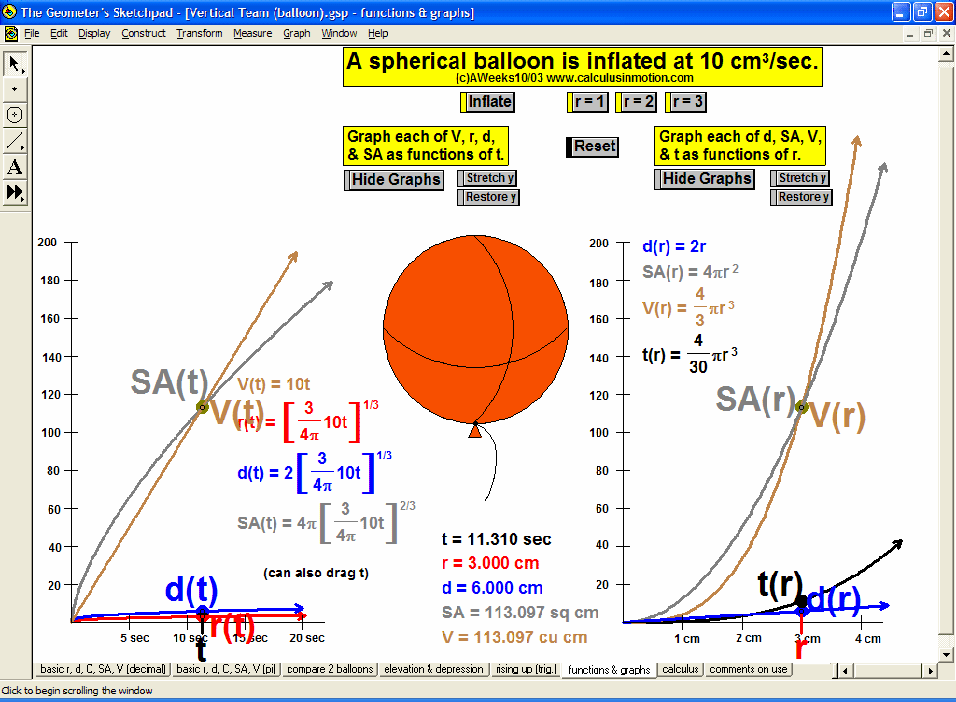
MORE APPLICATIONS & VERTICAL TEAMING
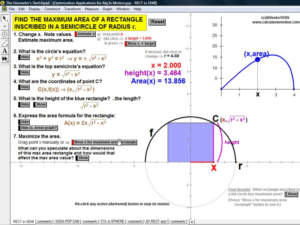
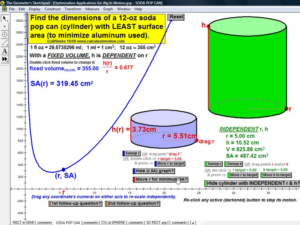
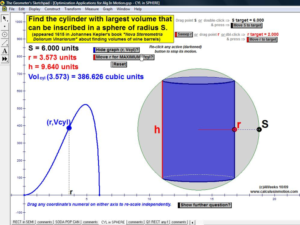
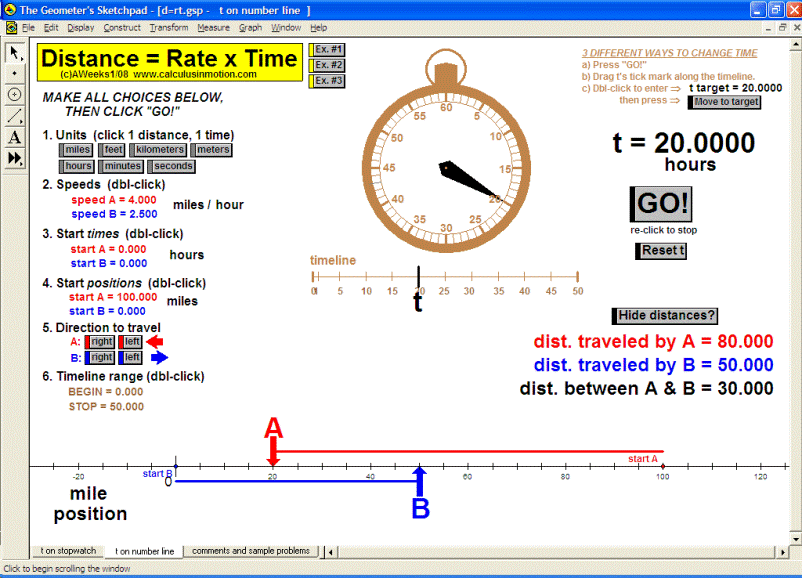
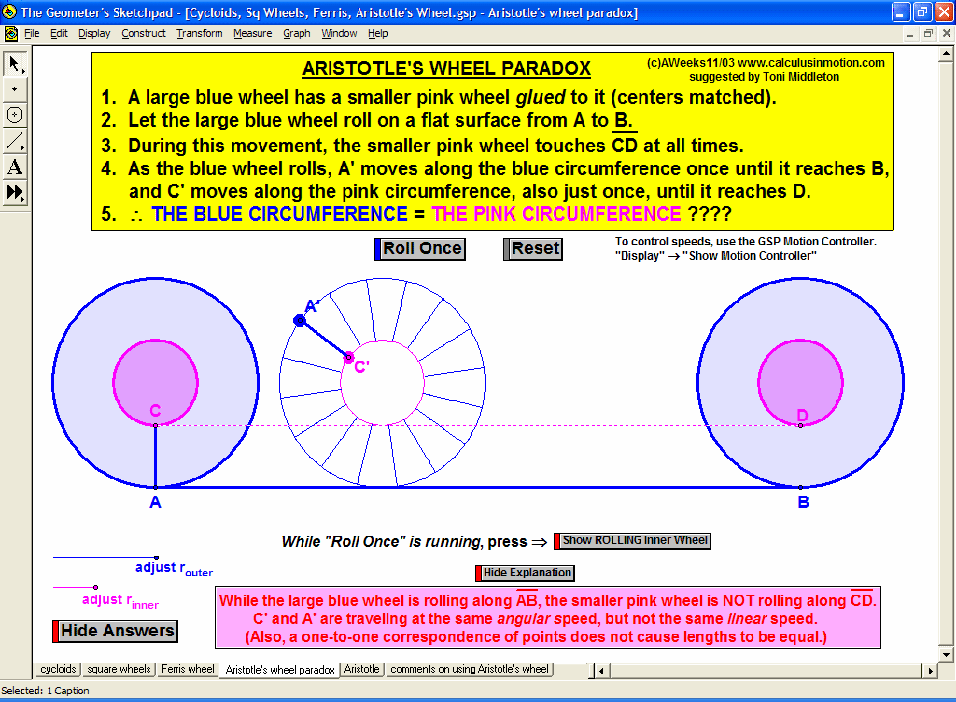
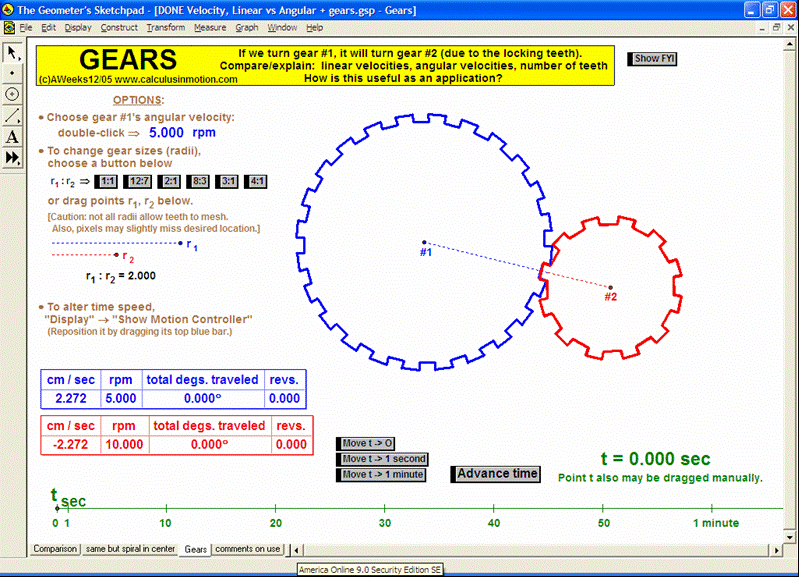
Build basic graphing sense using intriguing questions about real-world situations that animate at the click of a button. Thoroughly explore classic problems such as the “open box” (vary the size of squares removed from the corners of the original rectangle), the sliding ladder, flying kite, etc. As the level of the class increases, more and more features can be explored at the click of a button. Finally, even calculus students will benefit by experiencing the varying rates of change in familiar favorites – perfect for vertical teaming!