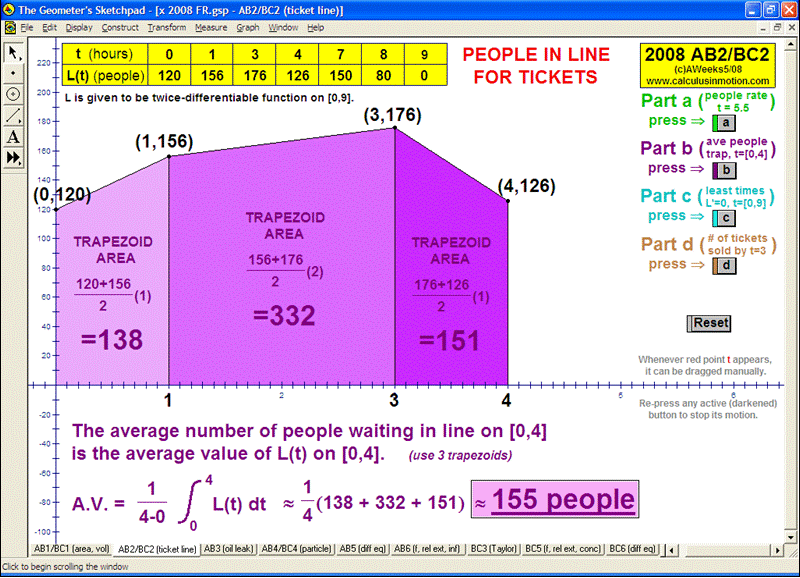
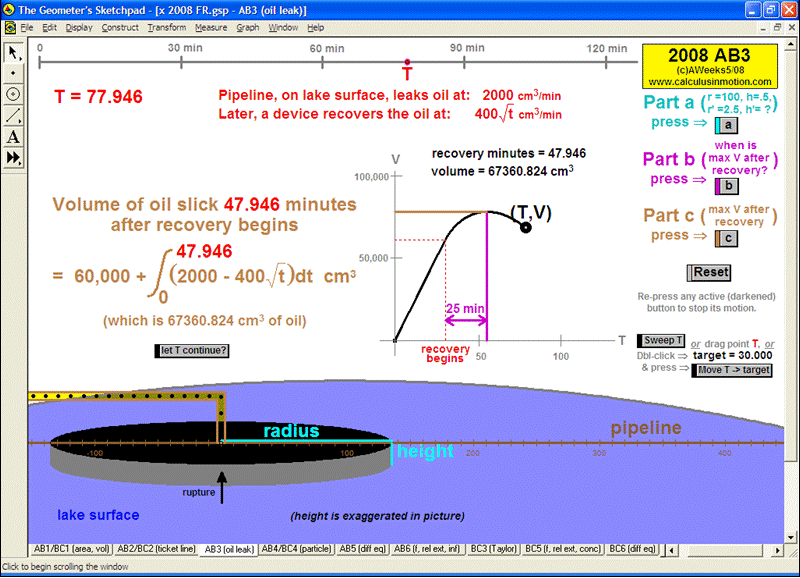
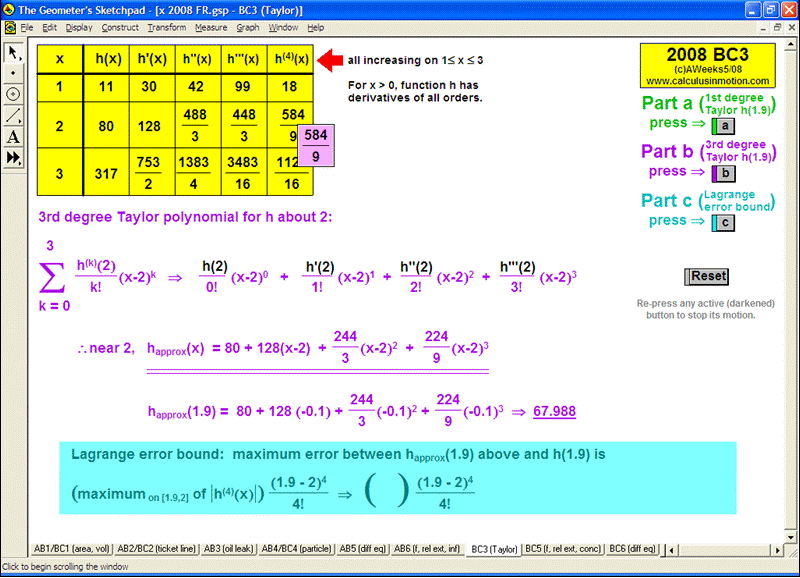
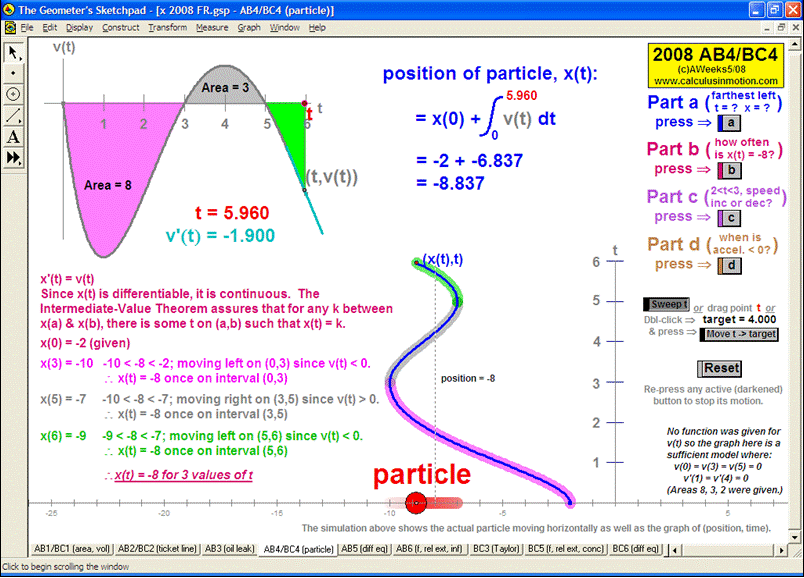
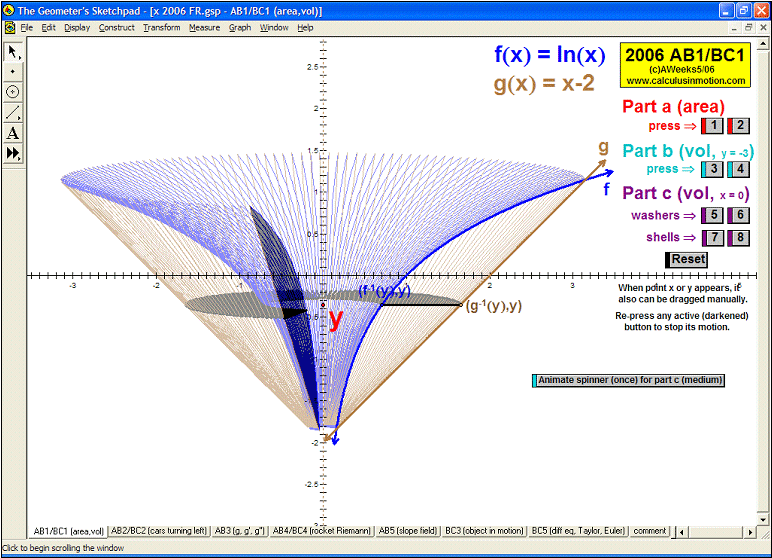
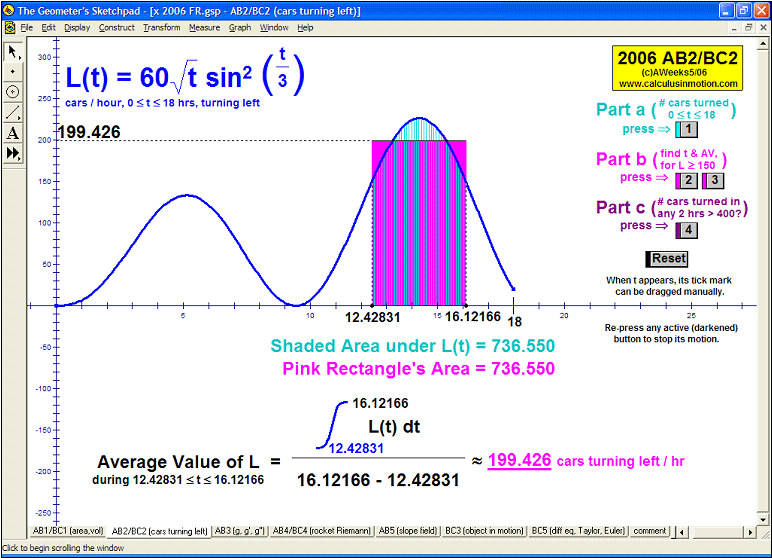
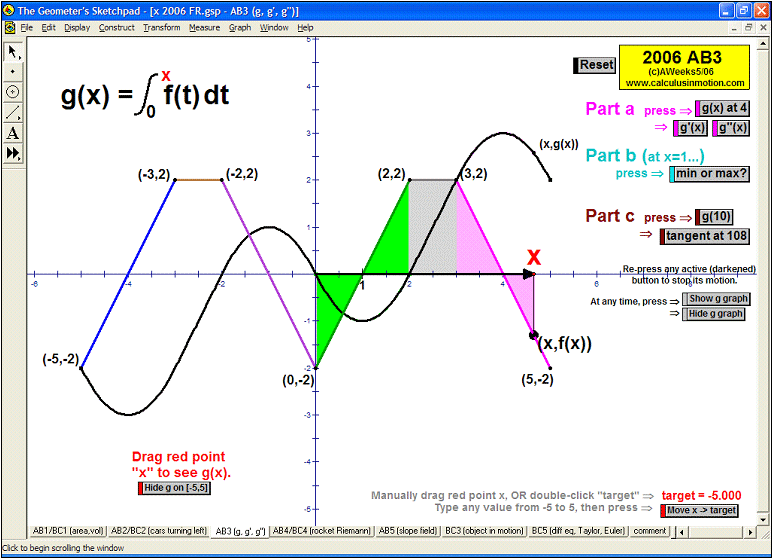
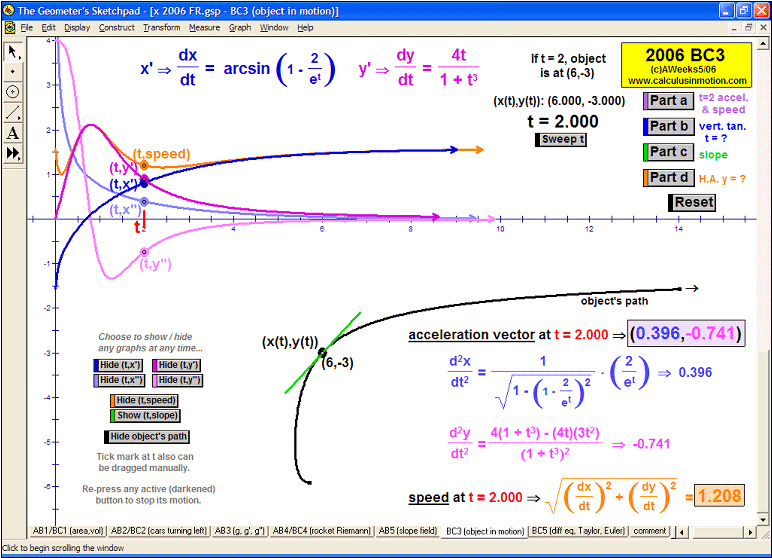
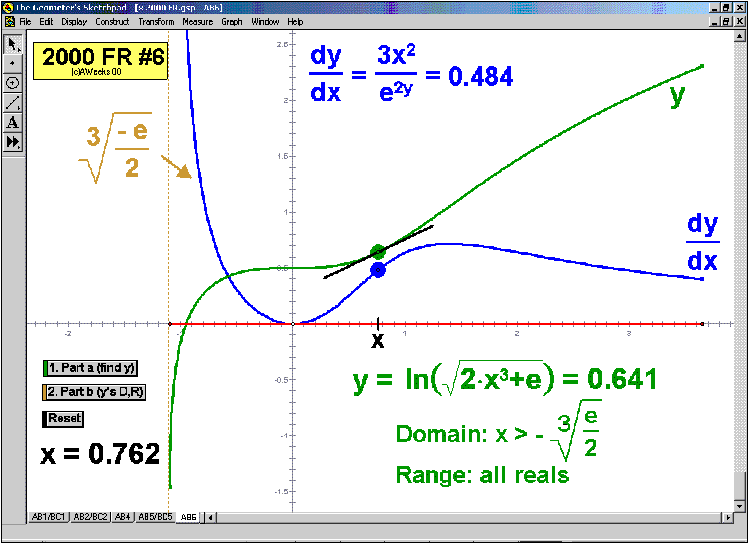
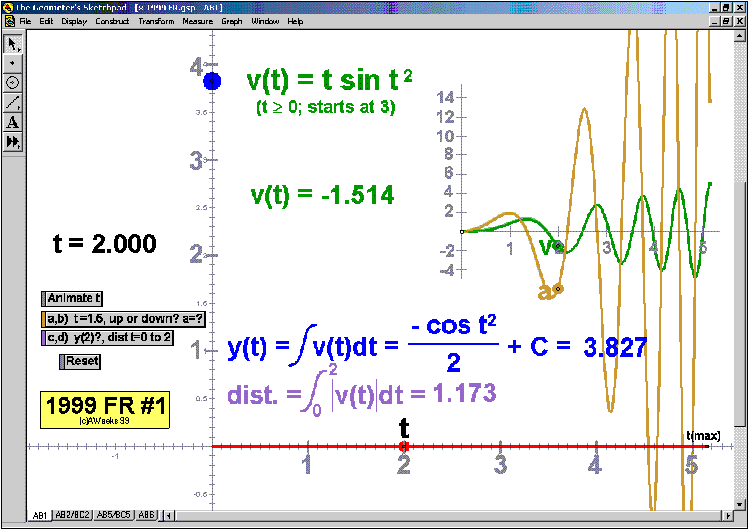
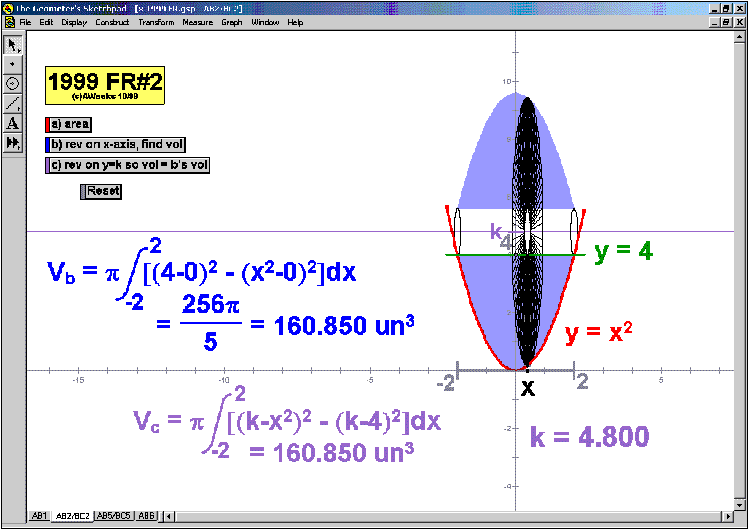
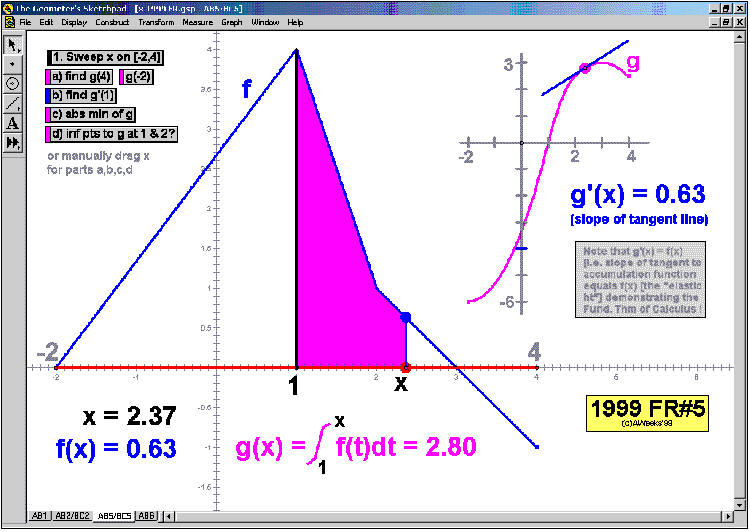
Whether teaching calculus at the introductory or AP level, at a high school or college, there is no better way to explore this rich study of movement and change than through interactive animation. Calculus In MotionTM animations have a basic license for 1 computer, but other licenses are available instead. They perform equally well on either the Windows or Macintosh platform. Although a detailed instruction manual is included (PDF format), most of the animations can be successfully run simply using the on-screen information.
NOTE: The animations are data files written in The Geometer’s Sketchpad, so Sketchpad must reside on your computer for the files to run – see full explanation in “Requirements” on the home page.
Galleries below are titled:
Arc Length
Area Between 2 Curves
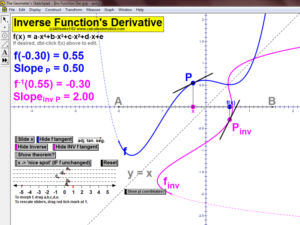
Def. of a Derivative / Def. of Integrations / Inverse Functions
Graphers
Limits & Continuity
Maclaurin & Taylor Series & Converging/Diverging
Optimization
Related Rates
Riemann Sums
Slope Fields & Euler’s Method
Theorems
Volumes on a Base
Volumes by Revolution
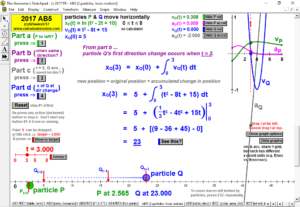
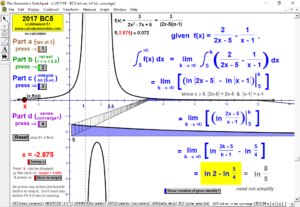
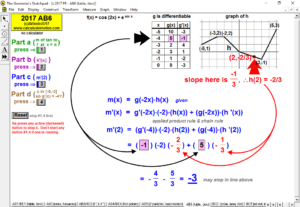
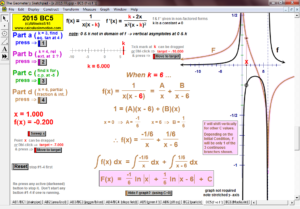
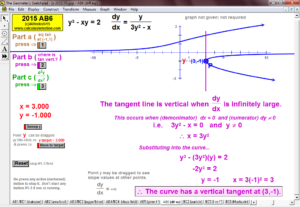
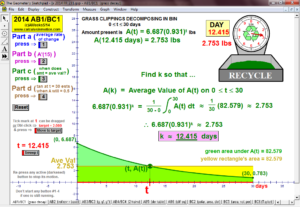
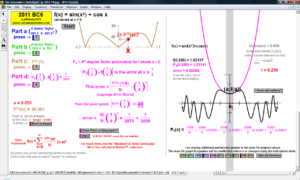
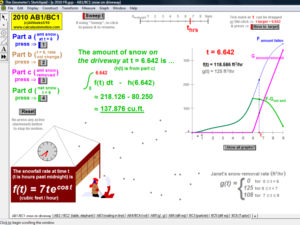
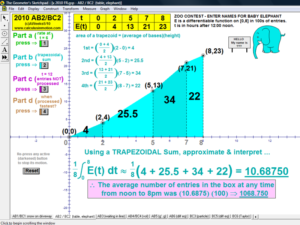
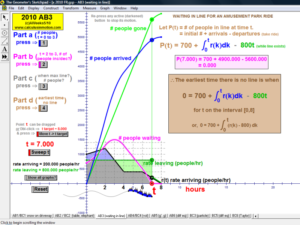
Animations to AP Calculus AB & BC Exams’ Released Free Response Questions 2023-1997 (except 2020, due to Covid changes) (Jump to FRs)
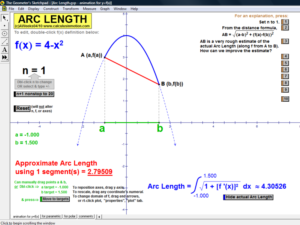
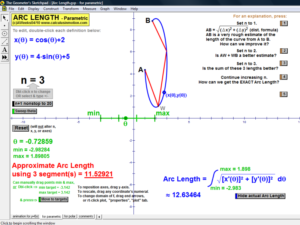
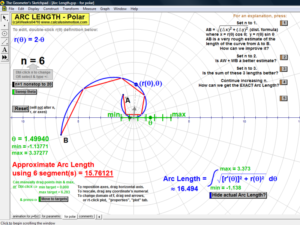
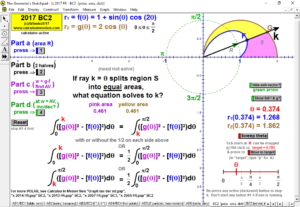
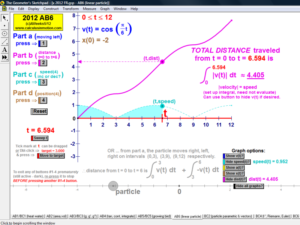
ARC LENGTH
Develop the idea of arc length using any f(x), parametric, or polar curve & any number of partitions.
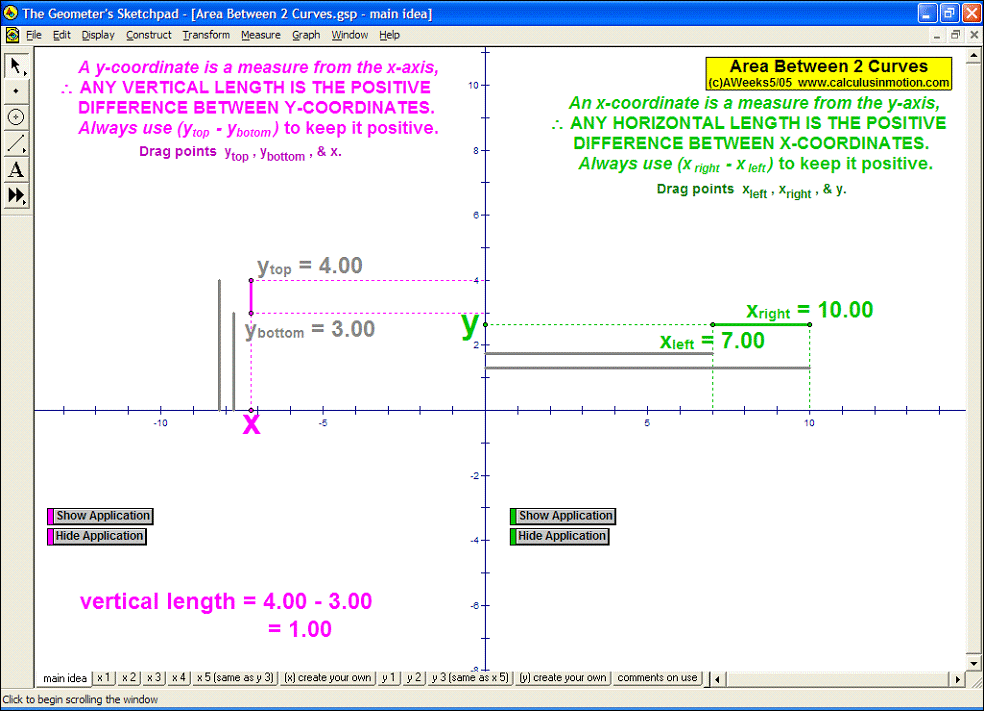
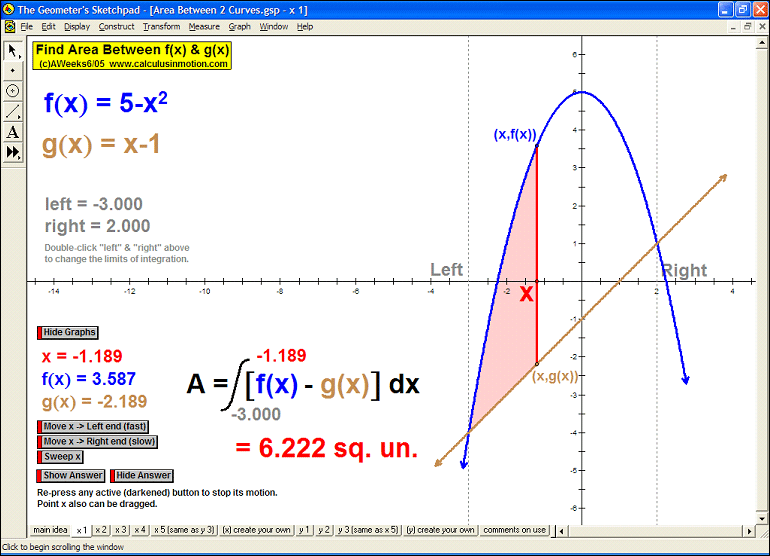
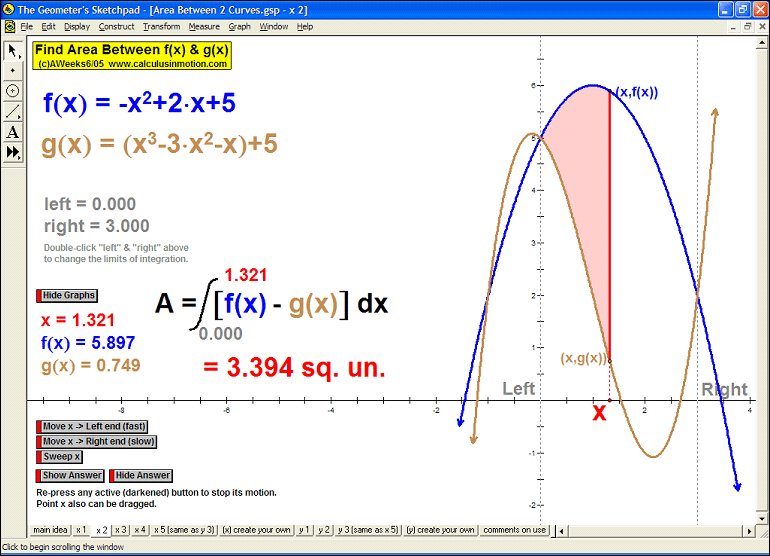
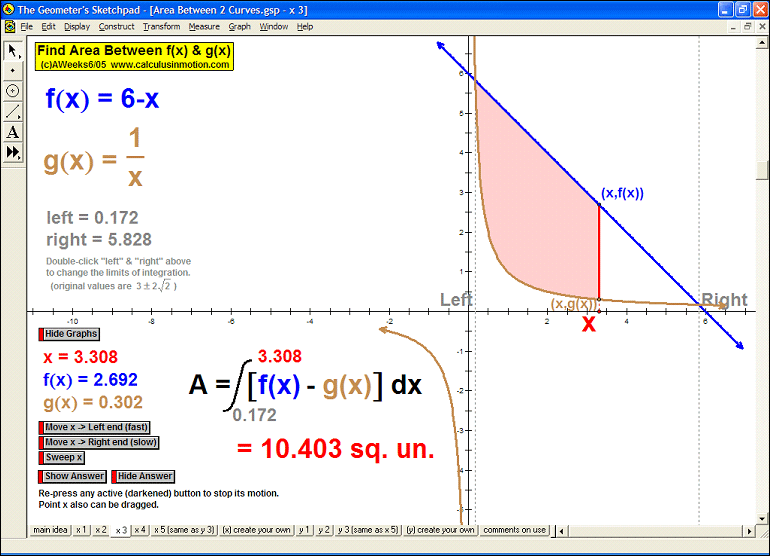
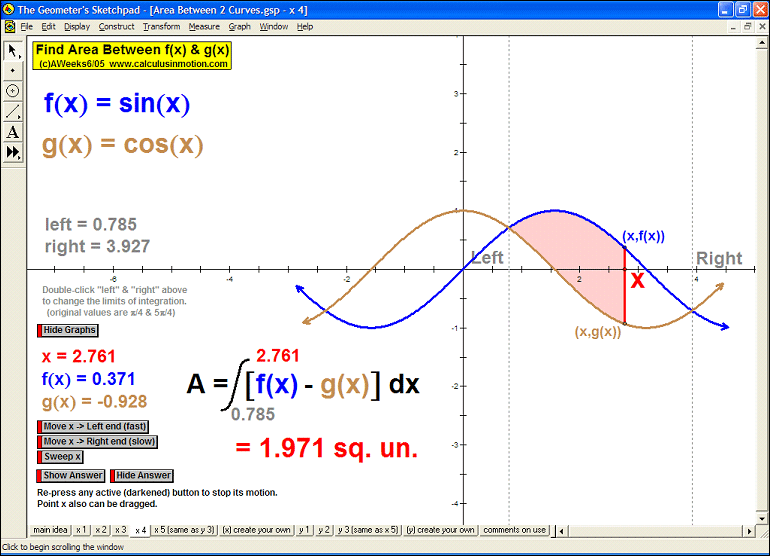
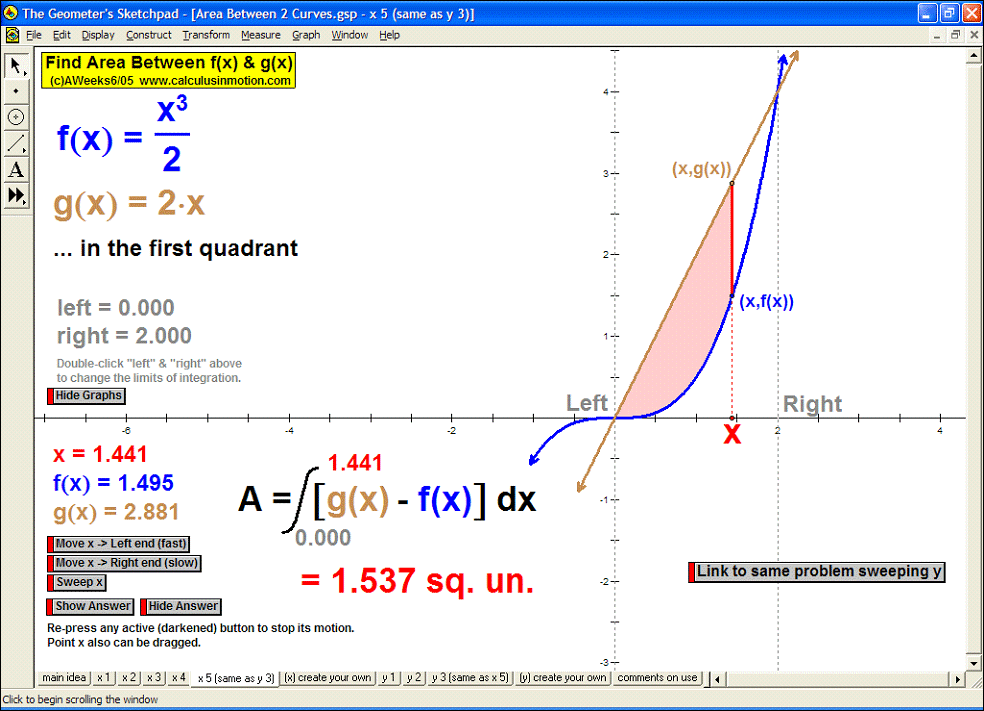
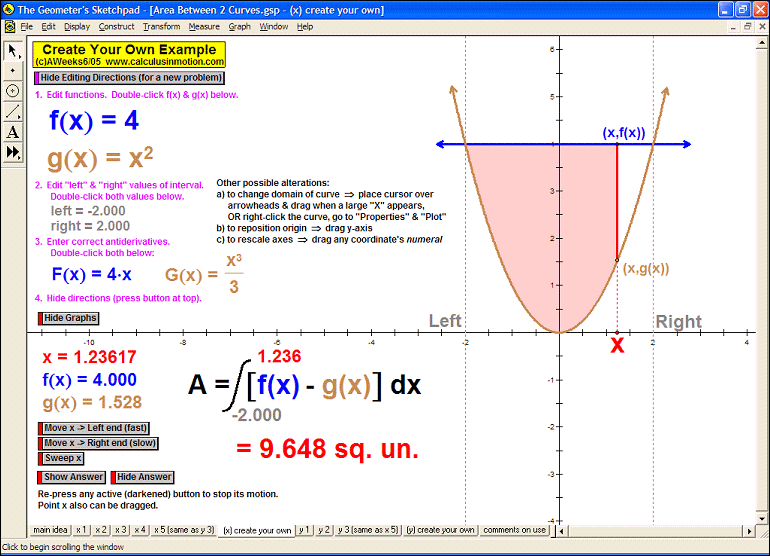
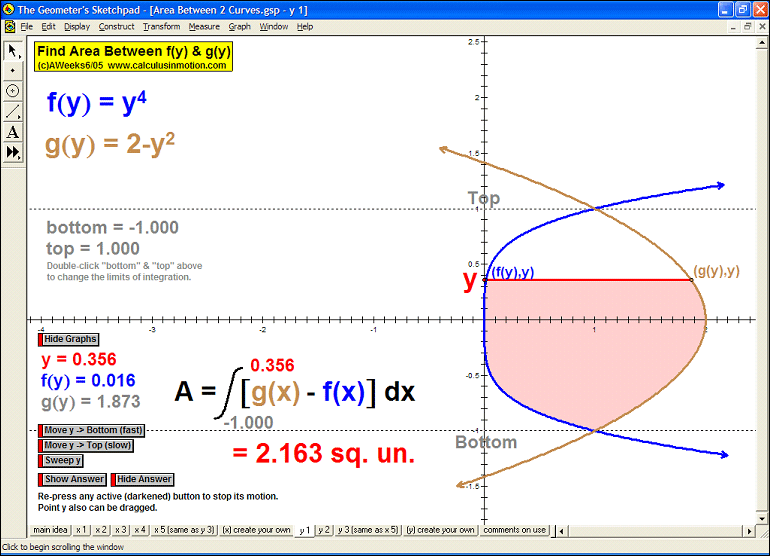
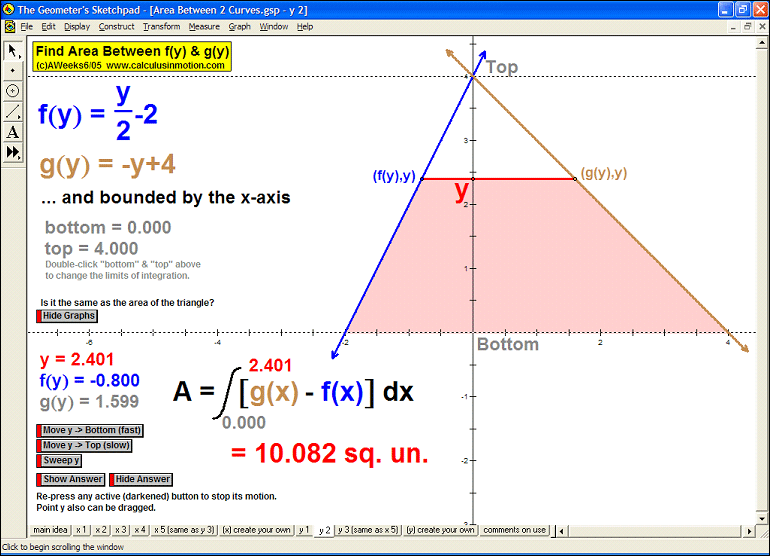
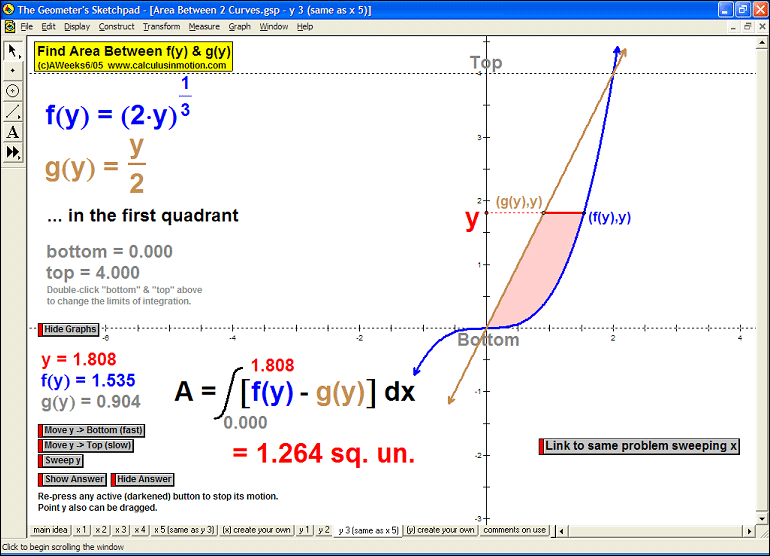
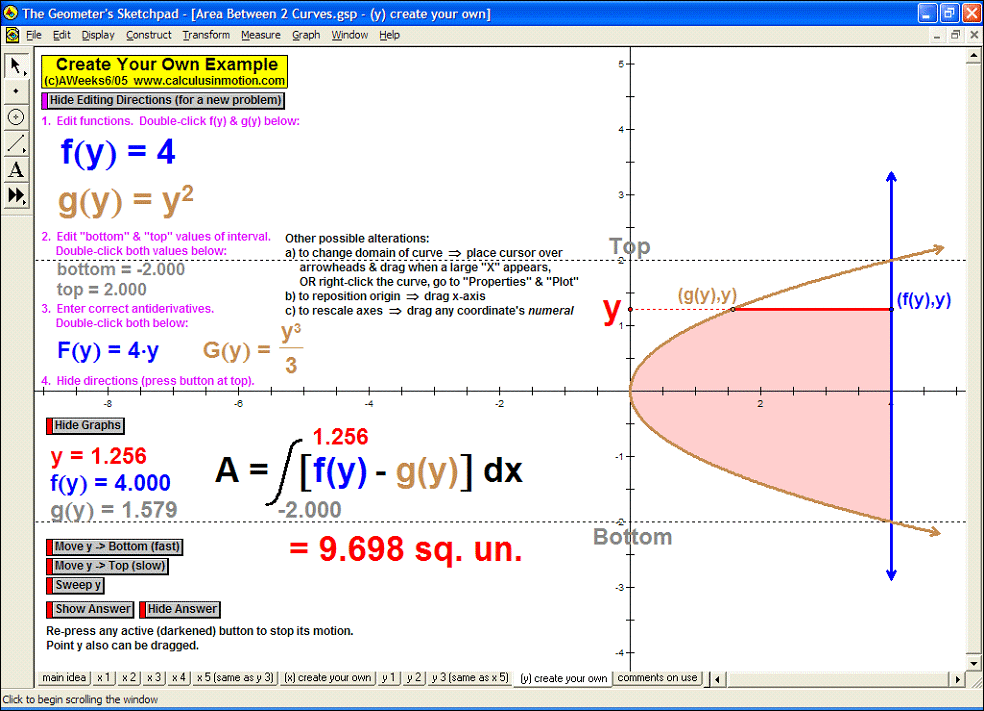
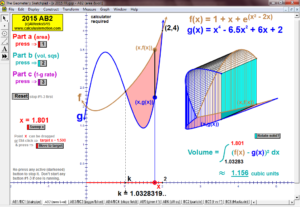
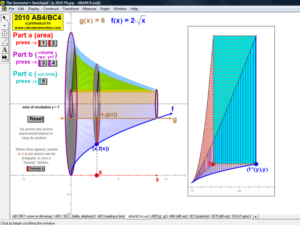
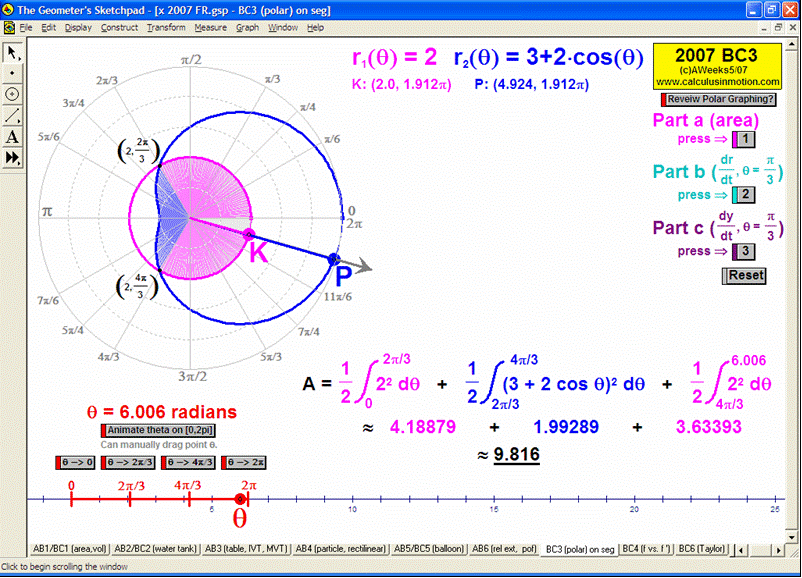
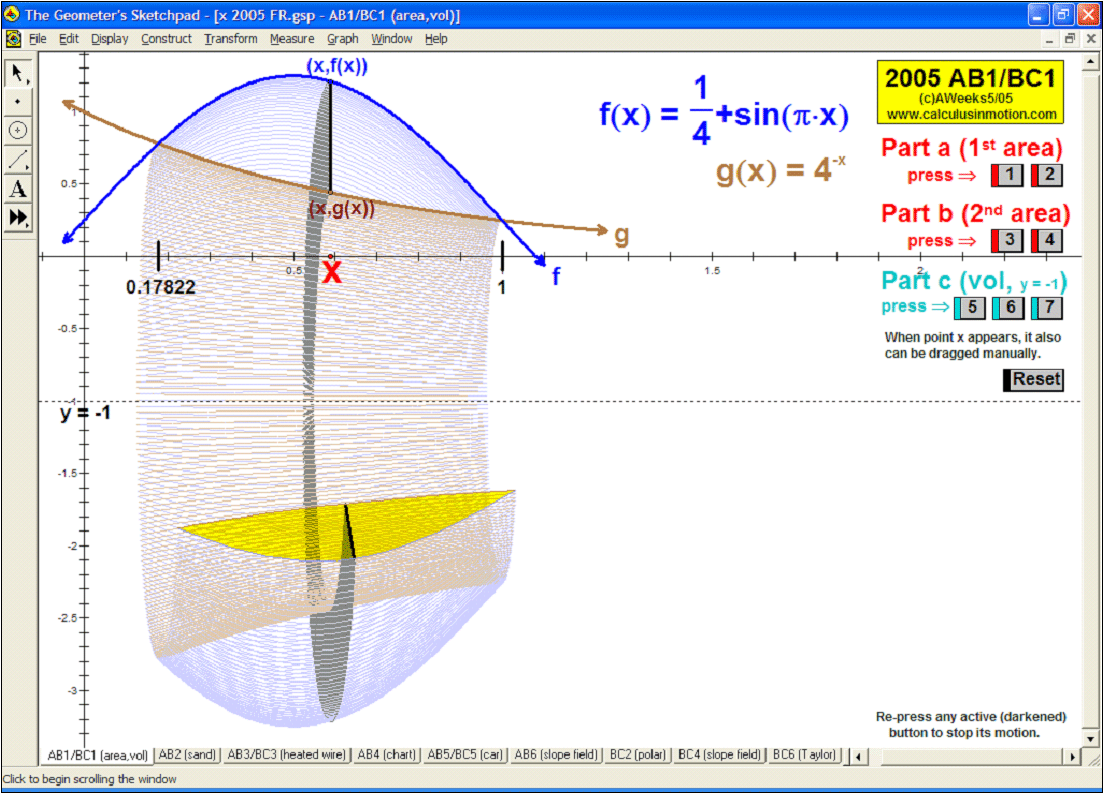
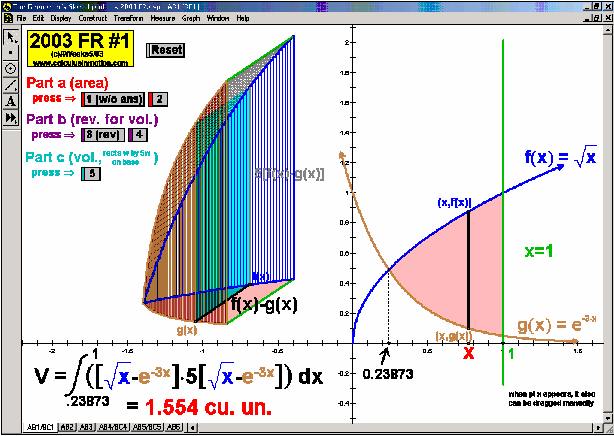
AREA BETWEEN 2 CURVES
Sweeping horizontally or vertically, the first animation explains the main idea, then 8 specifi
c examples
follow with changeable intervals, and finally, 2 animations (one for vertical sweeps and one for horizontal)
you can enter any desired curves as well as the boundaries of integration.
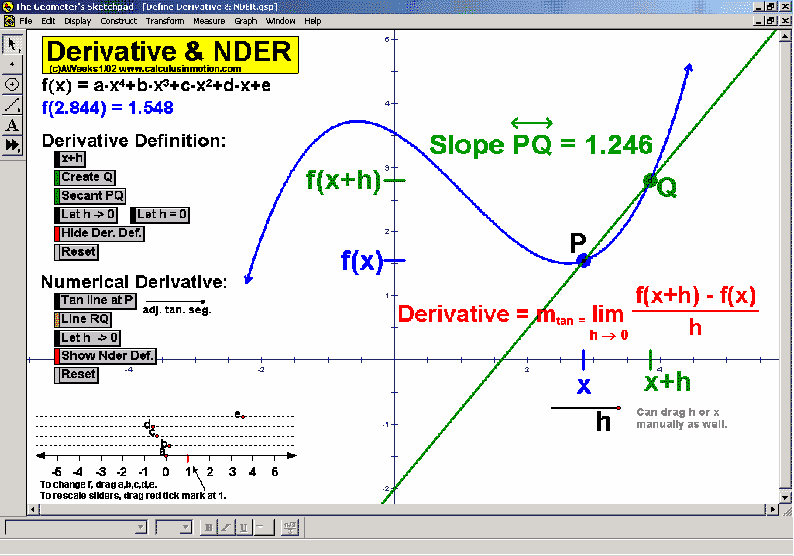
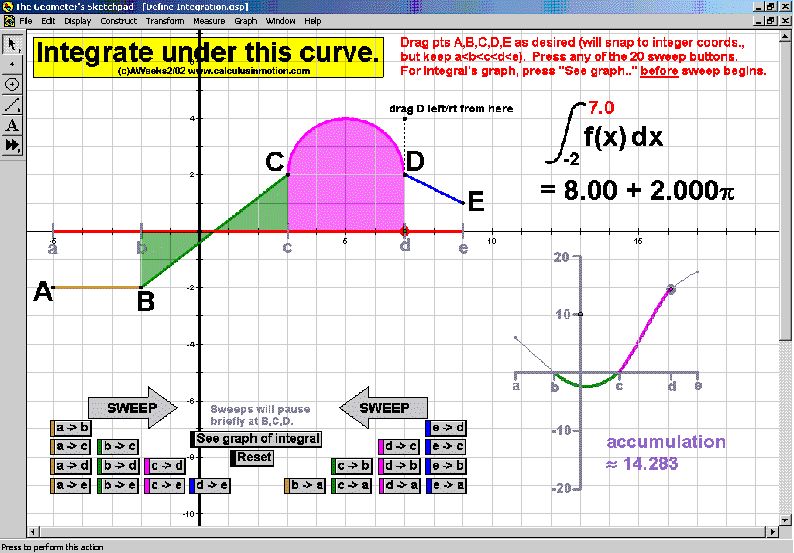
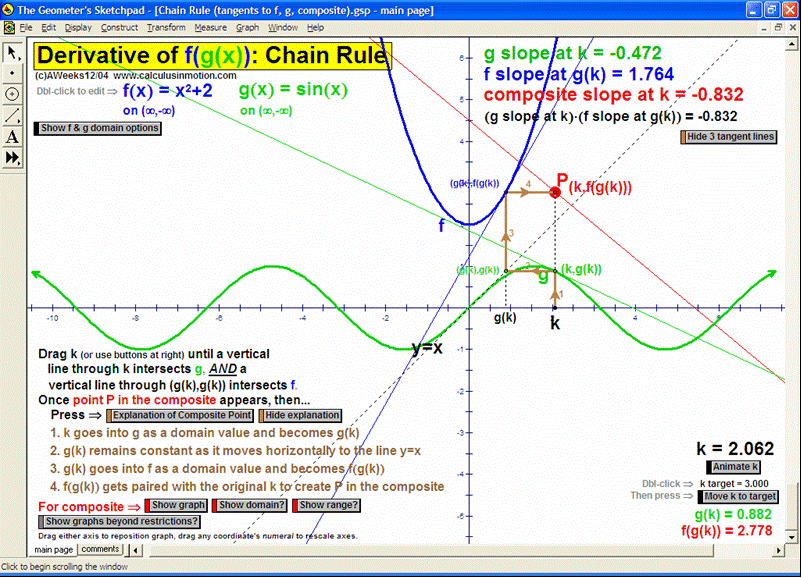
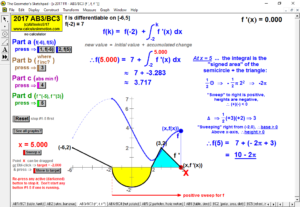
DEFINITION OF A DERIVATIVE ~ DEFINITION OF INTEGRATION ~ INVERSE FUNCTIONS
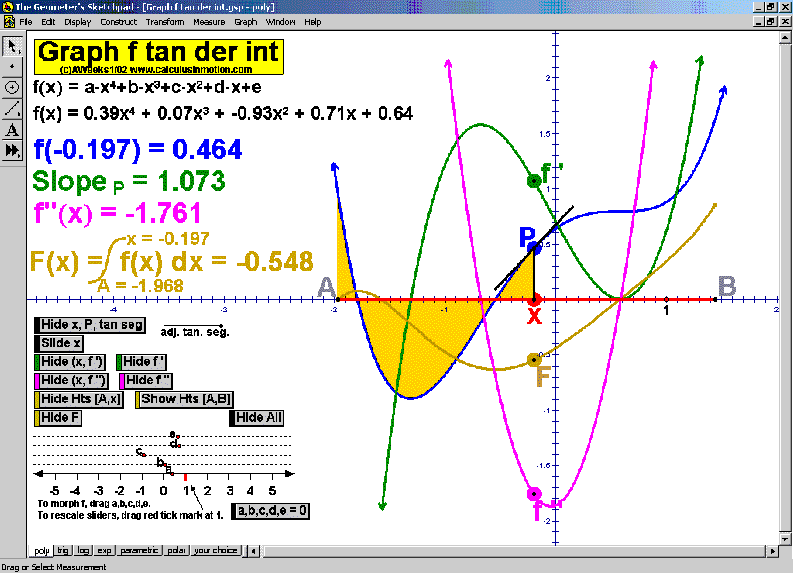
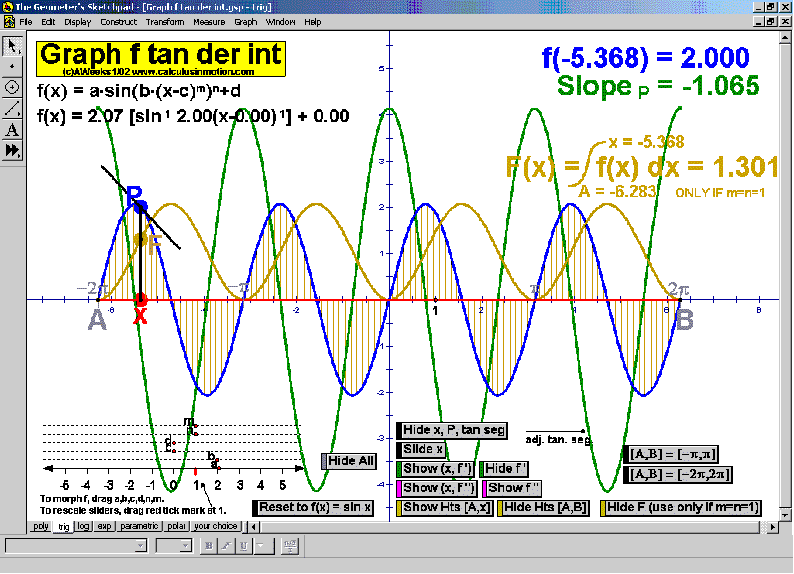
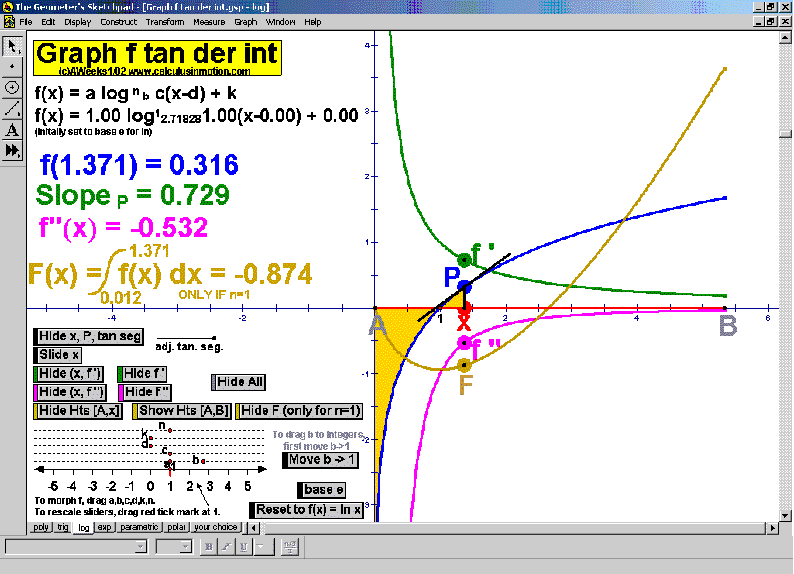
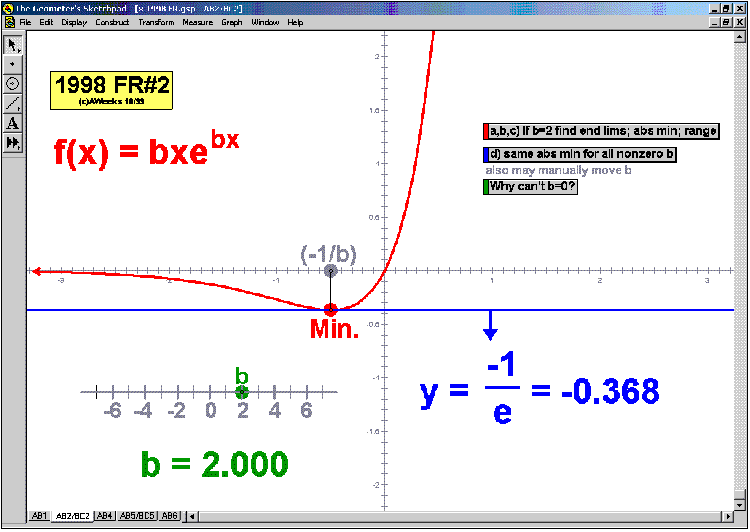
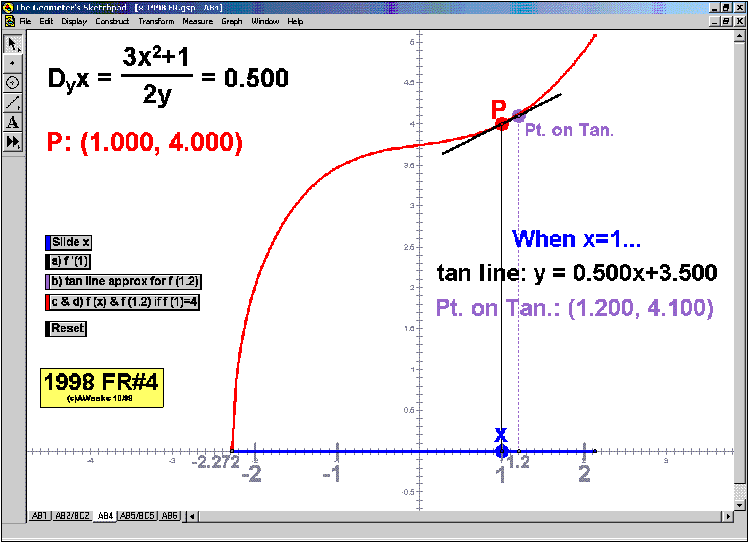
GRAPHERS
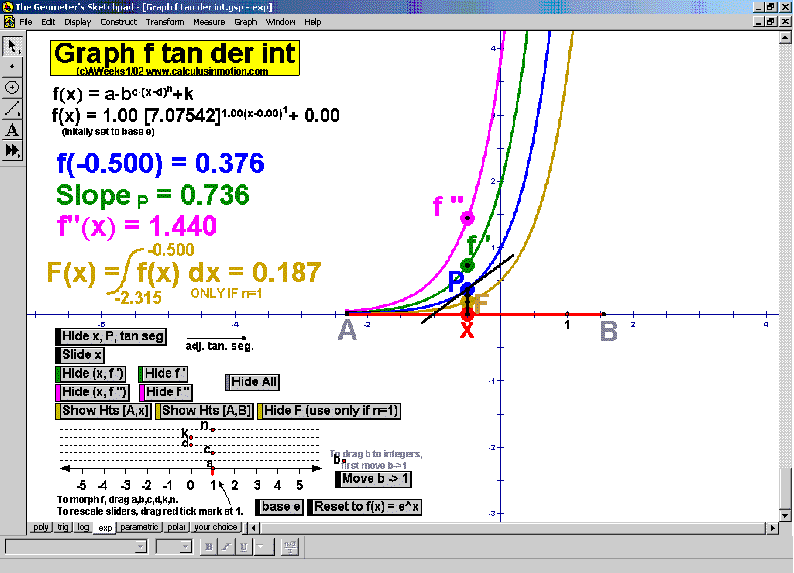
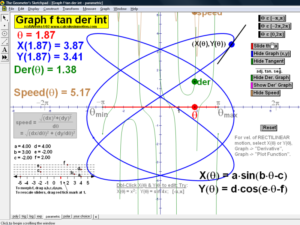
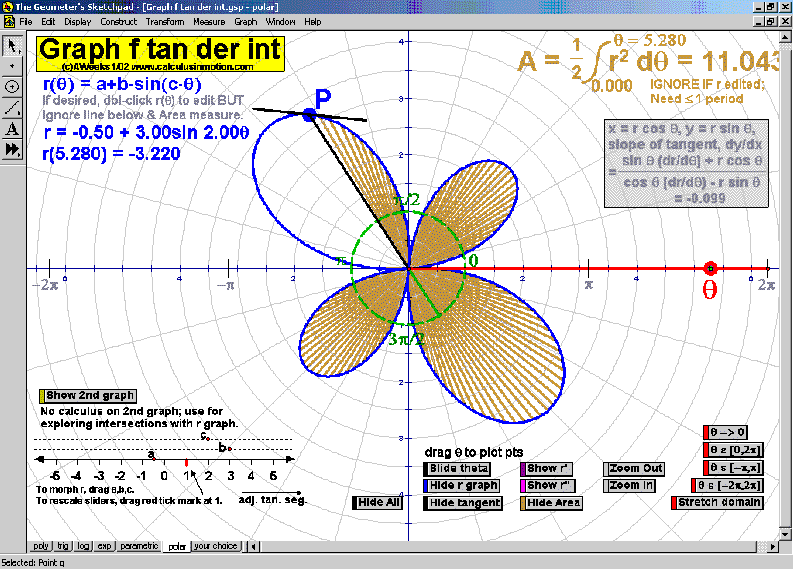
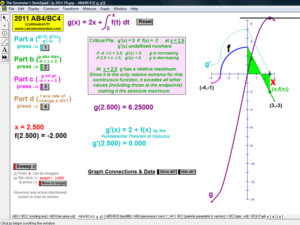
Explore slope using animated tangent lines. See any desired combination of f ‘, f ‘’, area, and F.
“Morph” each graph using sliders. A 7th animation (not shown below) allows the user to enter any
desired function and applies all of the same animated features to it. (*also for precalculus)
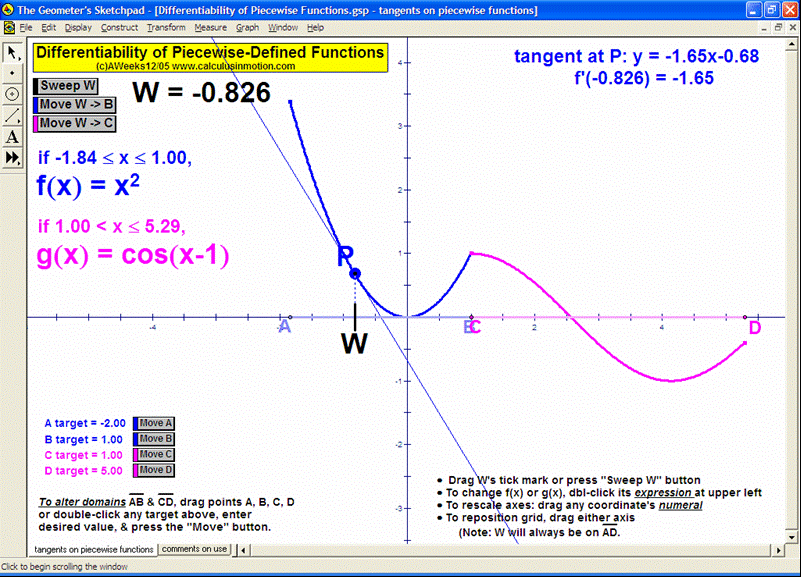
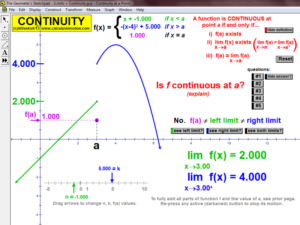
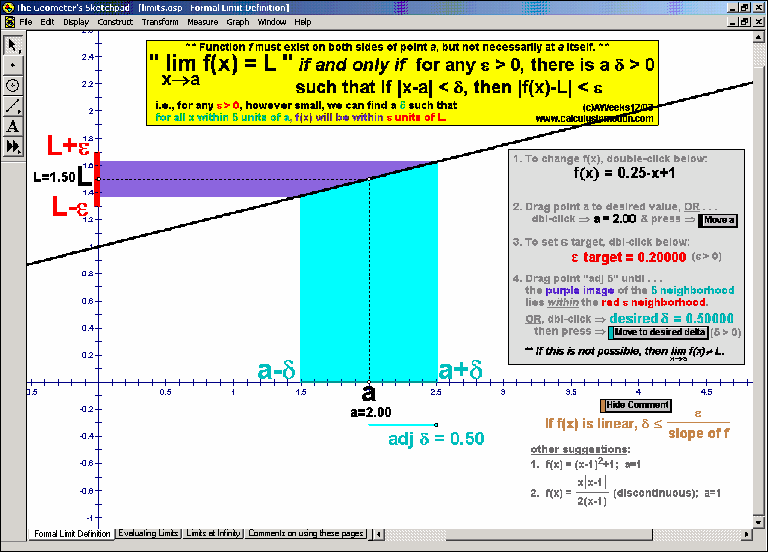
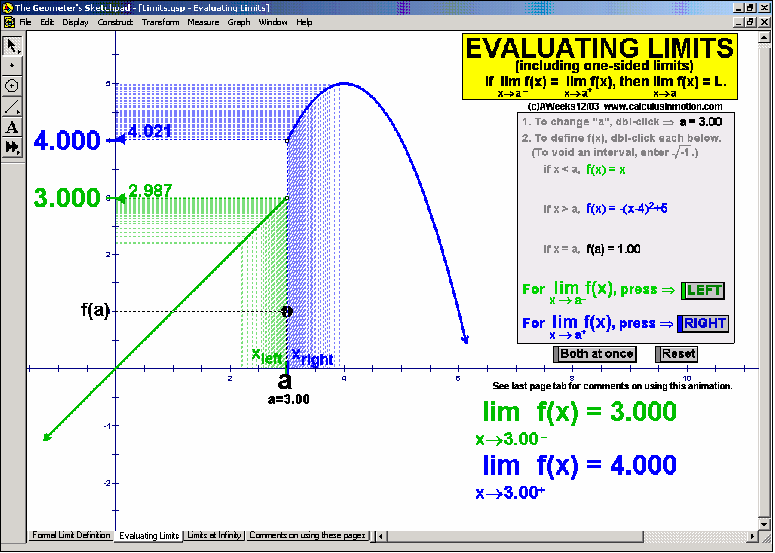
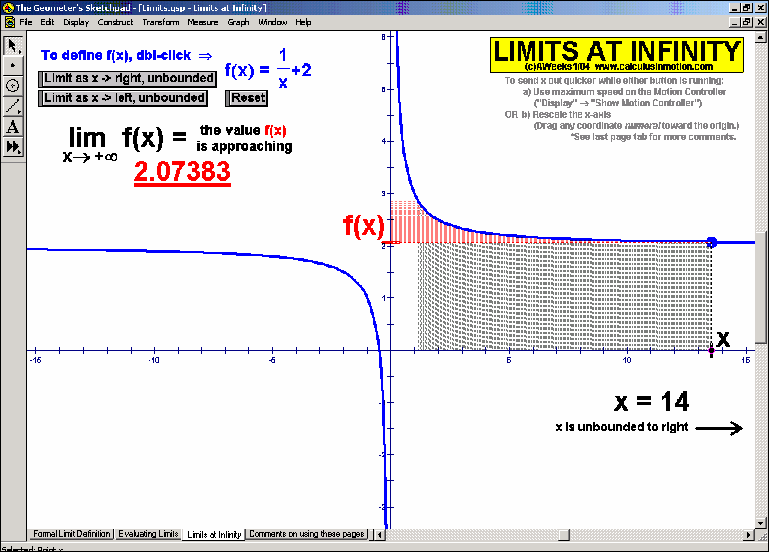
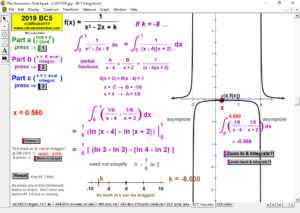
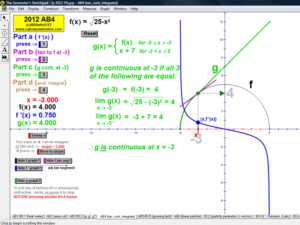
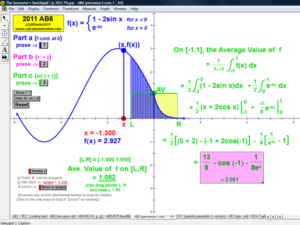
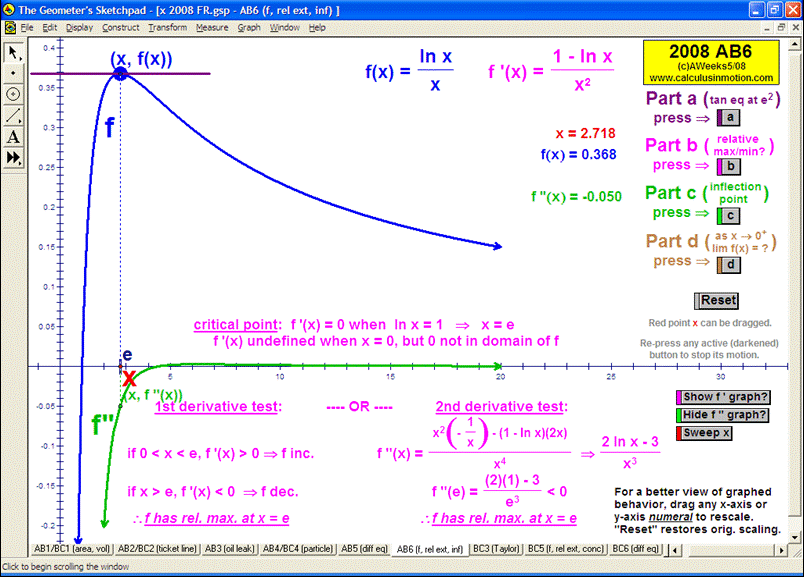
LIMITS AND CONTINUITY
Explore the ε, ∂ definition of limits and the definition of continuity.
Evaluate the limits (full, left-hand or right-hand) of any function (including piece-wise defined) as x →a or as x→±∞
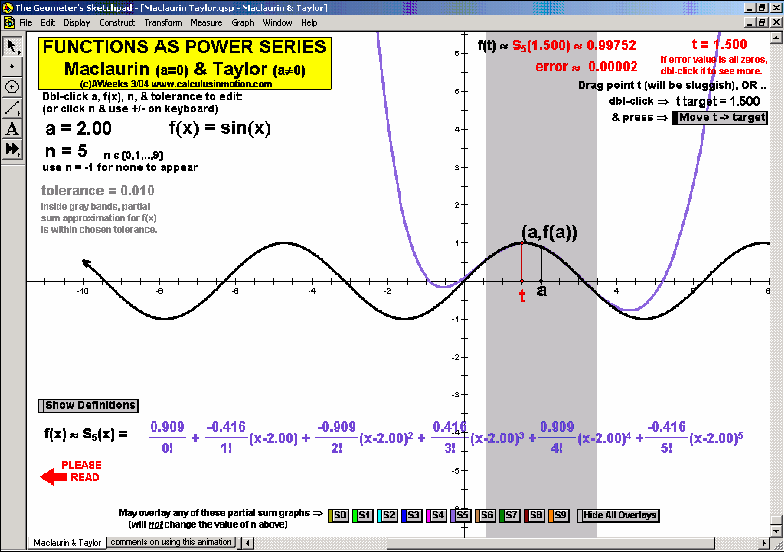
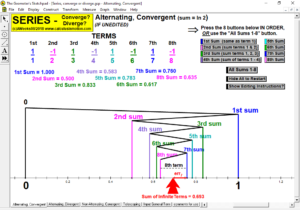
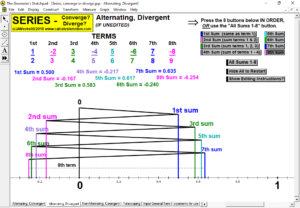
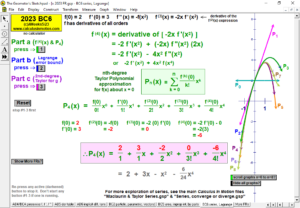
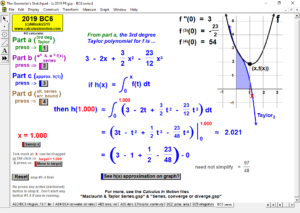
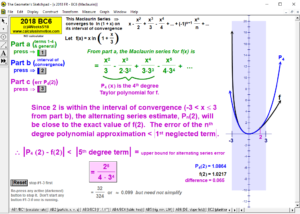
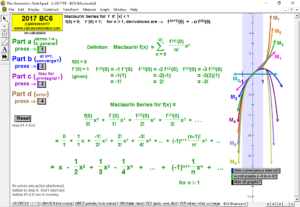
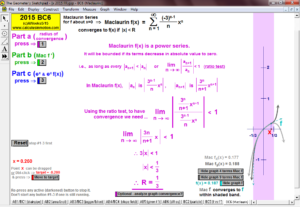
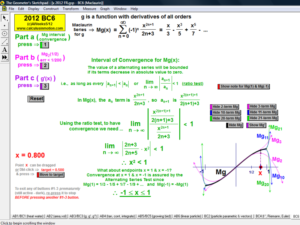
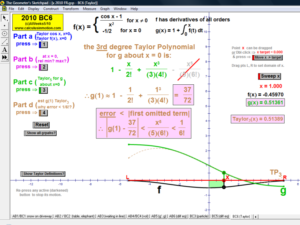
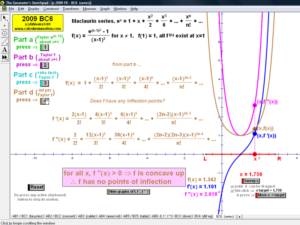
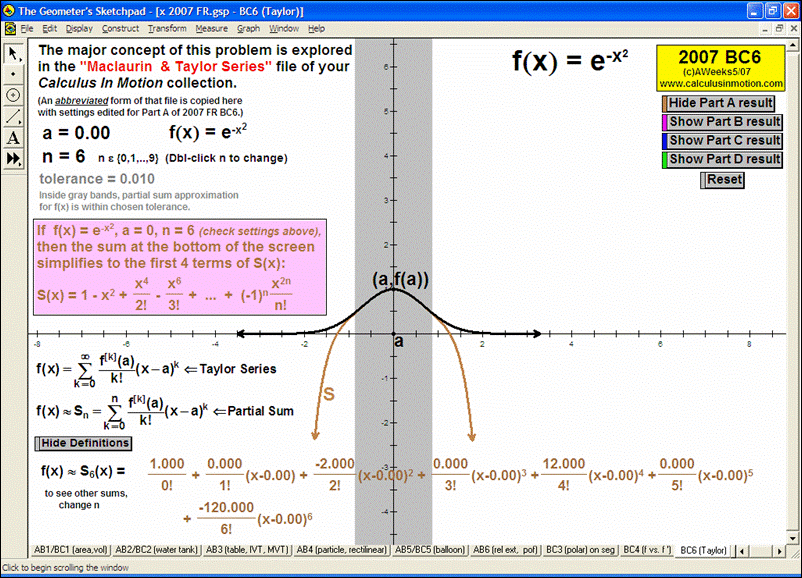
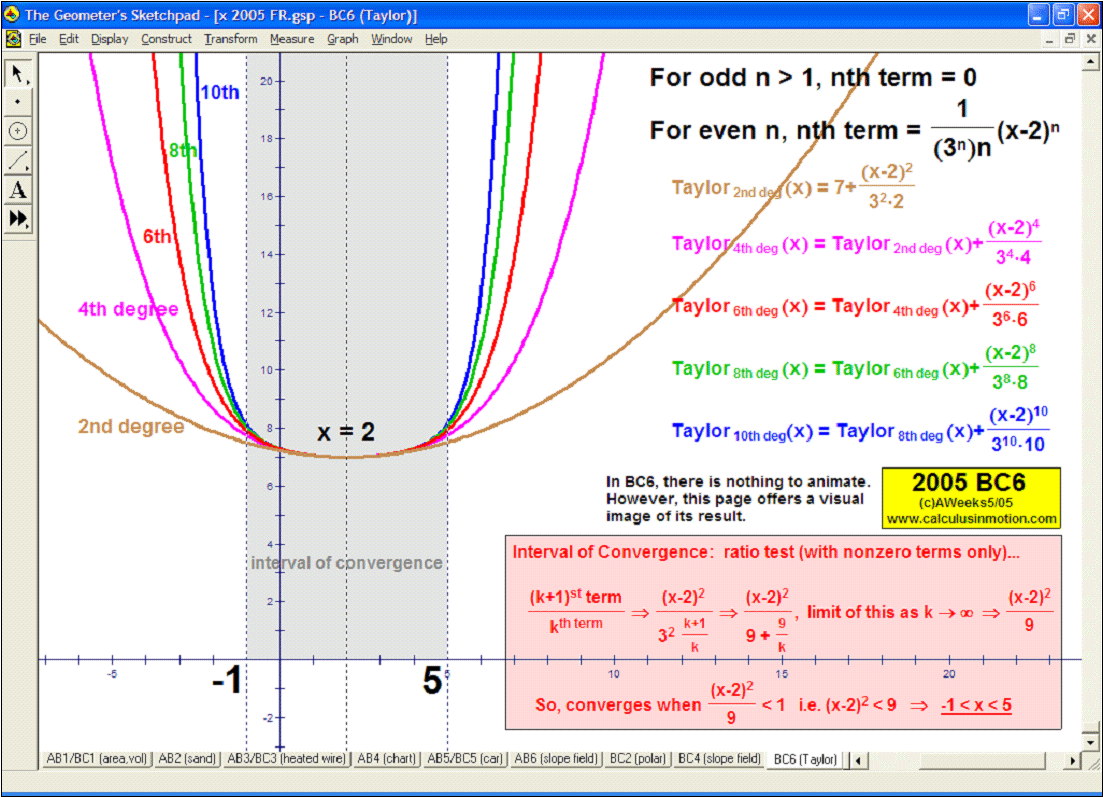
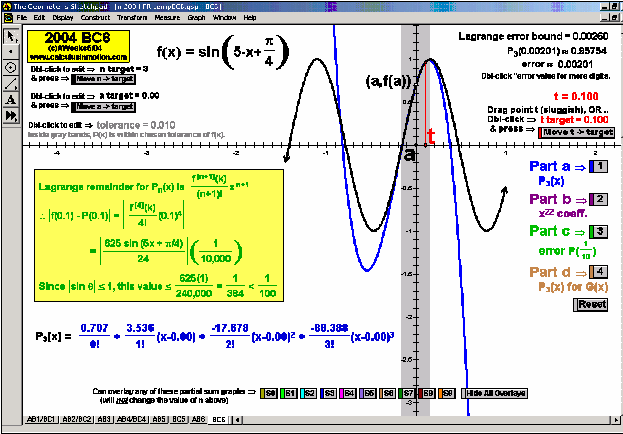
MACLAURIN AND TAYLOR SERIES & CONVERGING/DIVERGING
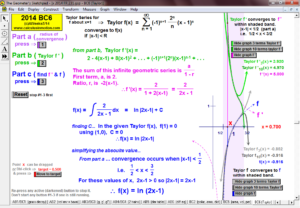
Enter any f(x). Overlay a Maclaurin or Taylor Series polynomial of degree n & use it to approximate the value of f(x) at any point t. Vertical gray bands show where the power series is within a chosen tolerance to f(x). As n increases, the band widens.
Explore convergence or divergence of various types of series.
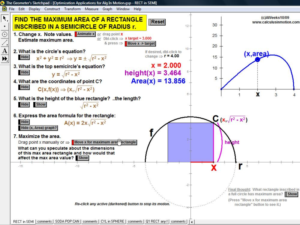
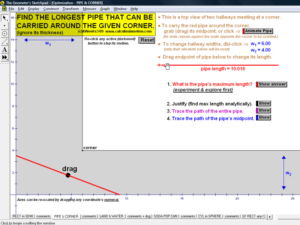
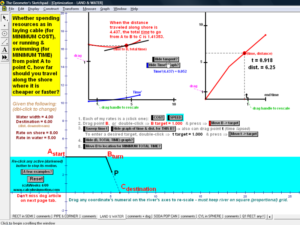
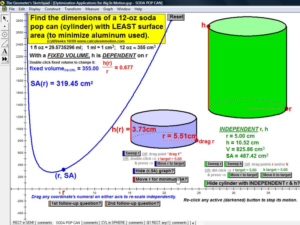
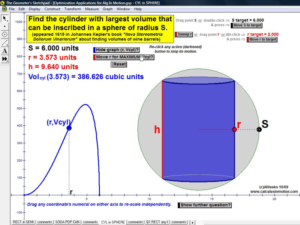
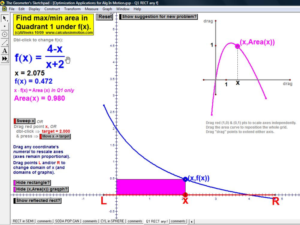
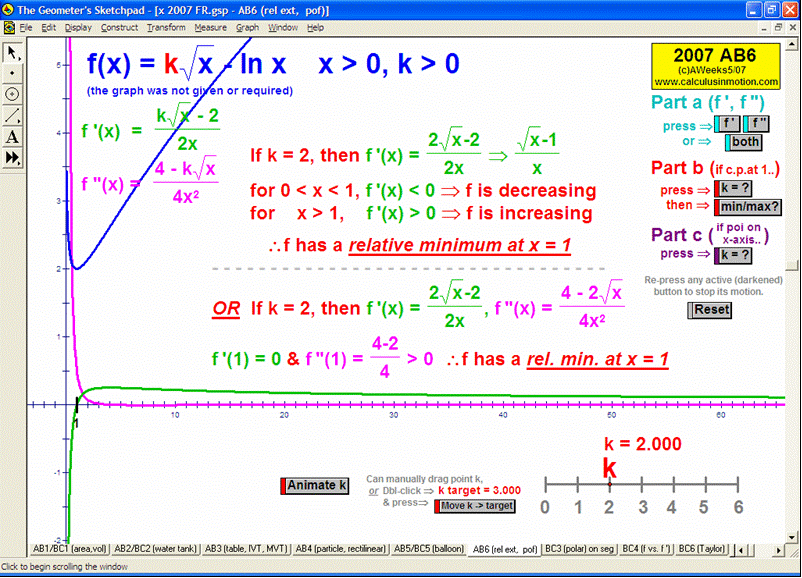
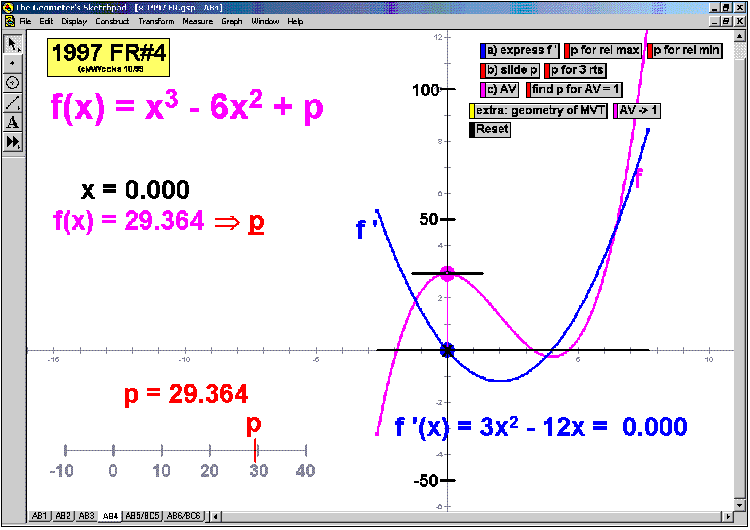
OPTIMIZATION
Interact with various classic applications to find the most, lerasdy, cheapest, fastest, etc.
Graphed data includes tangent line & derivative analysis.
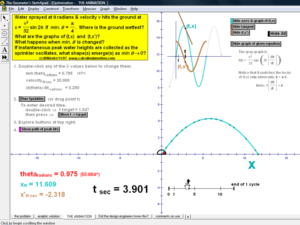
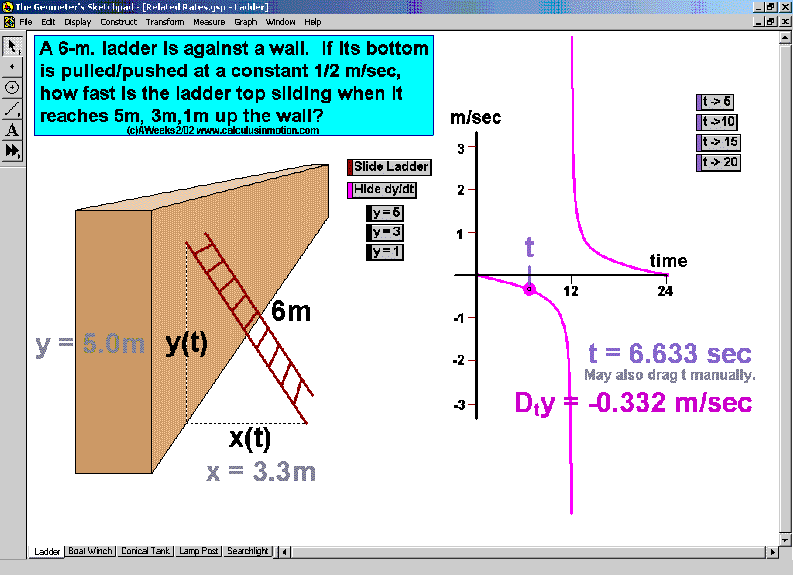
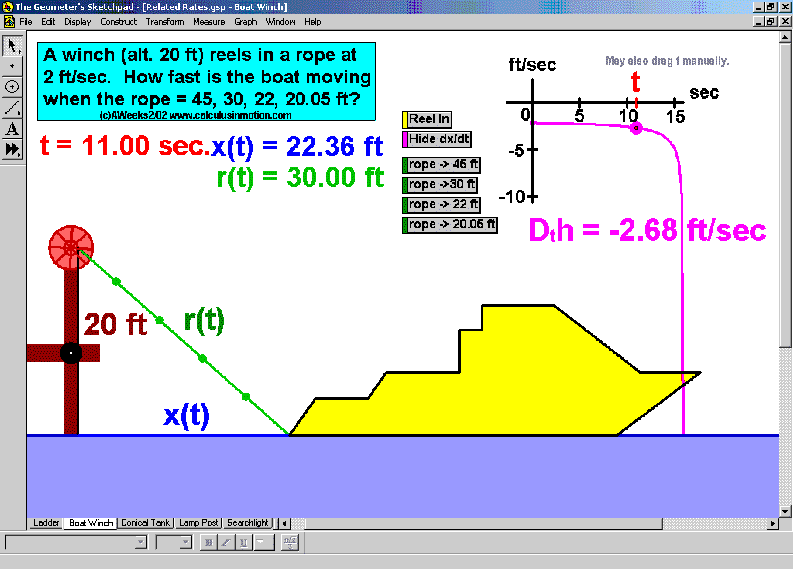
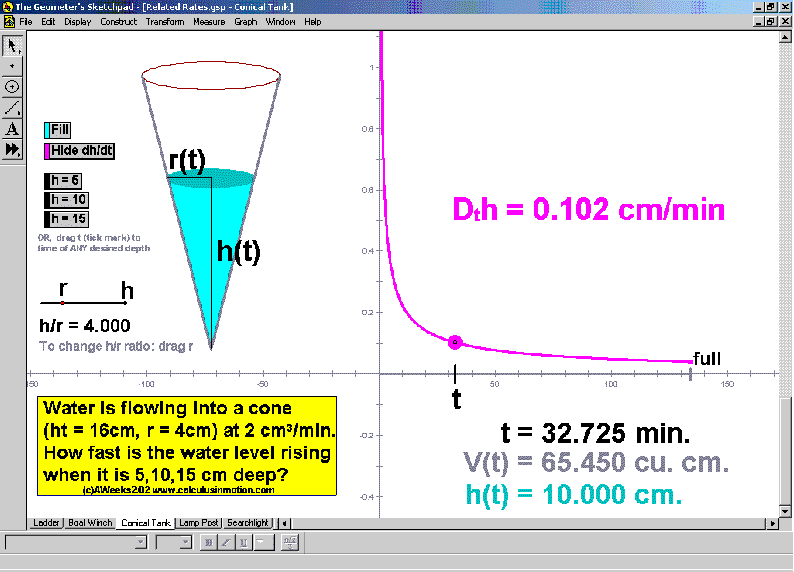
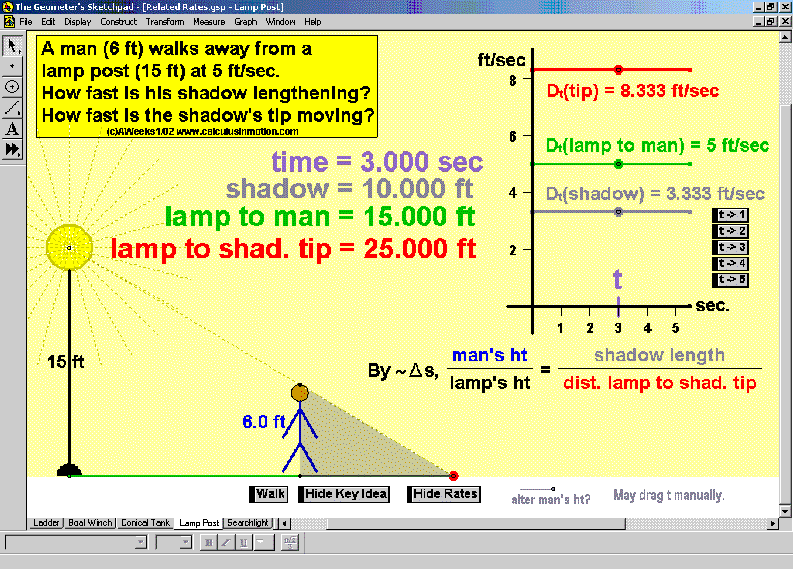
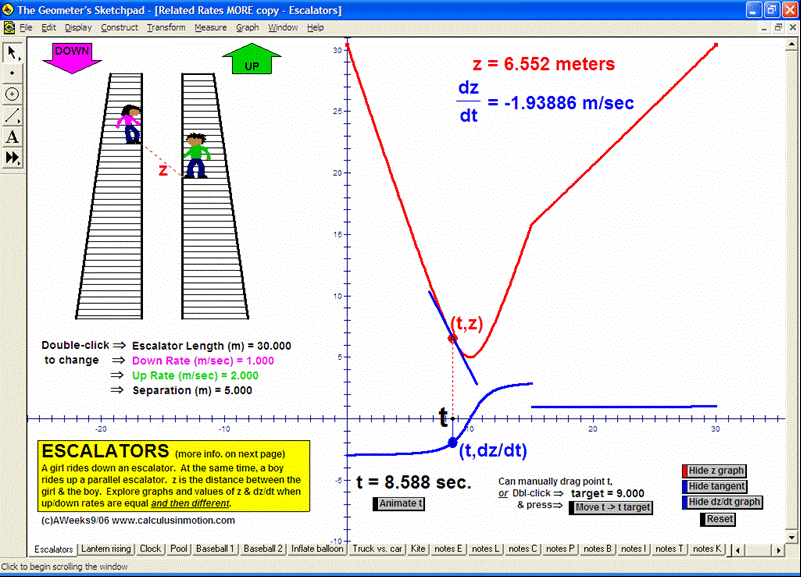
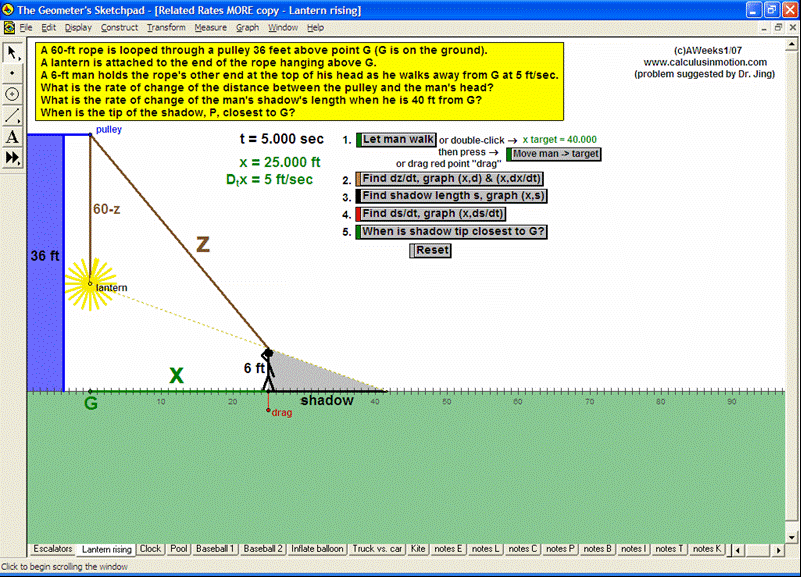
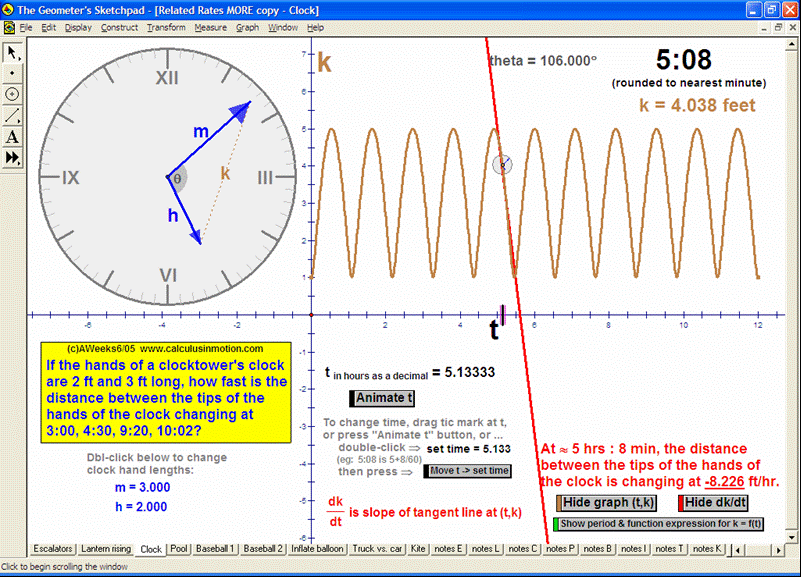
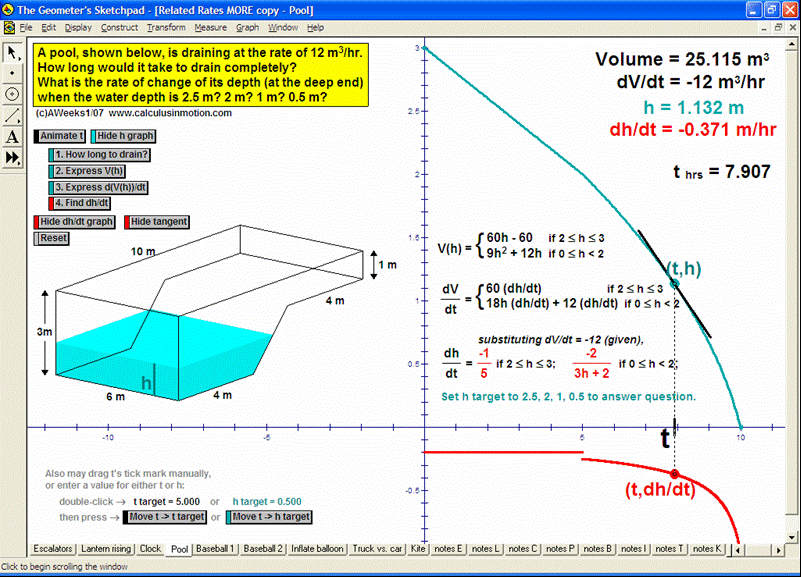
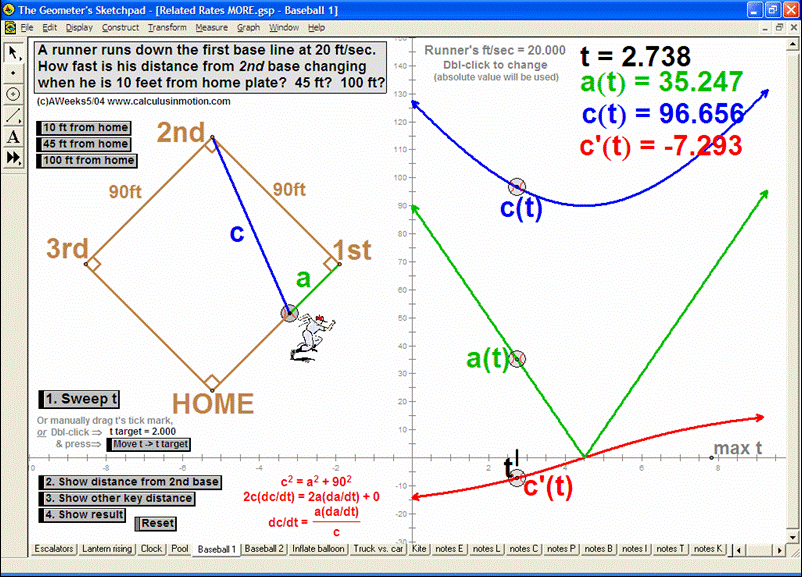
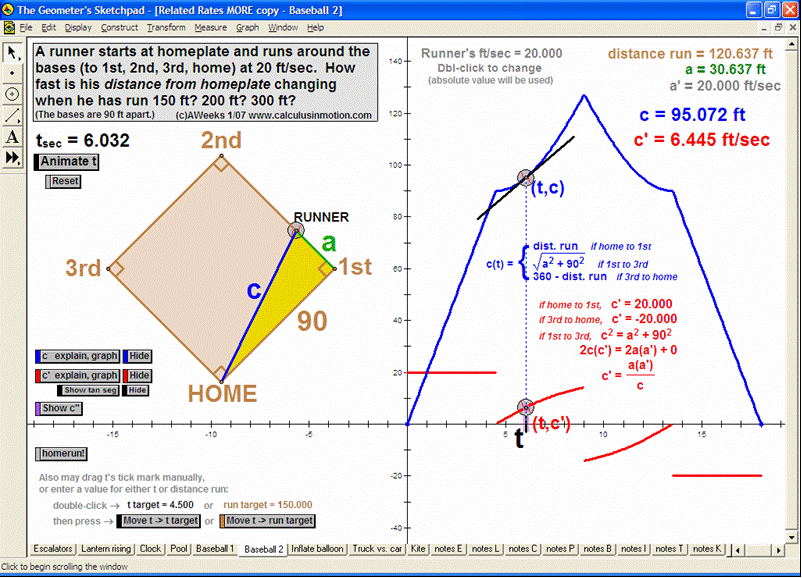
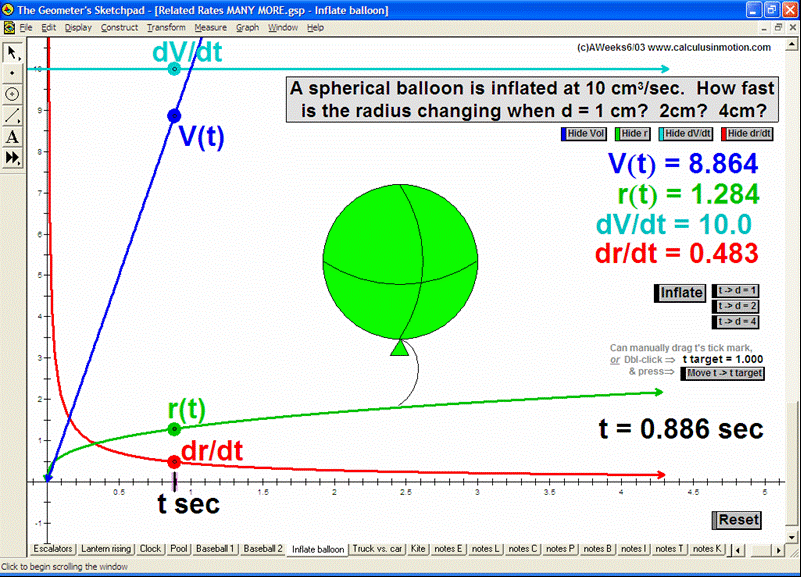
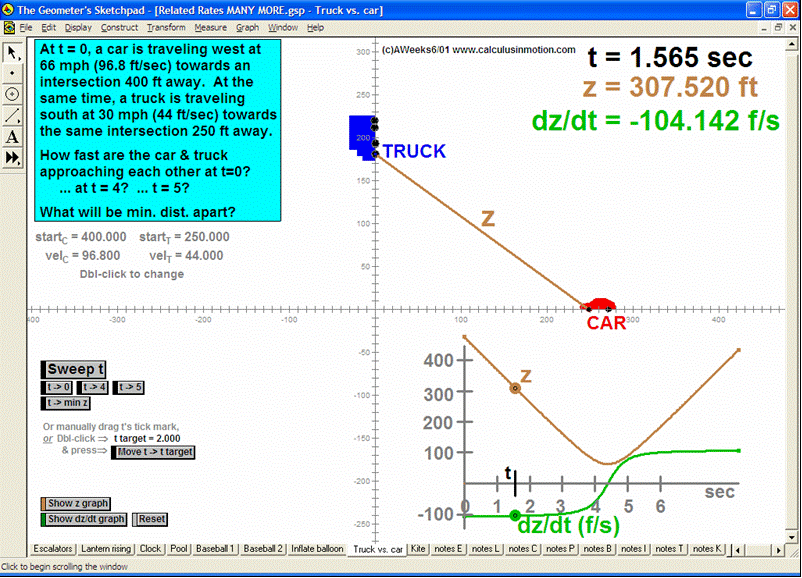
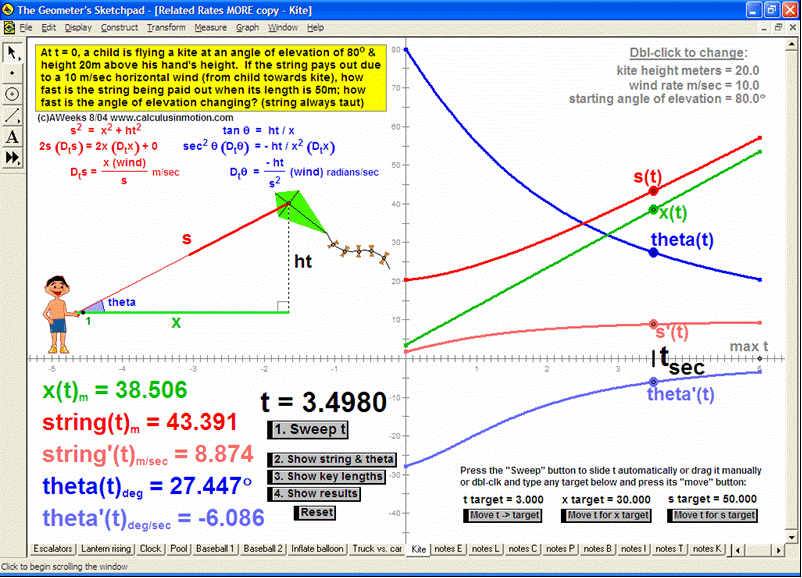
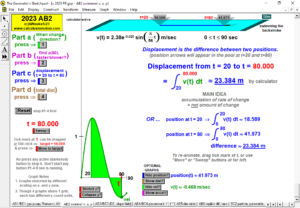
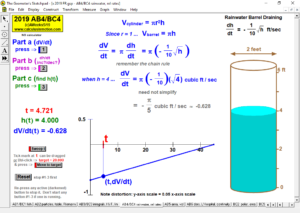
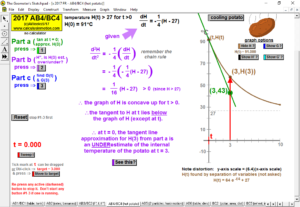
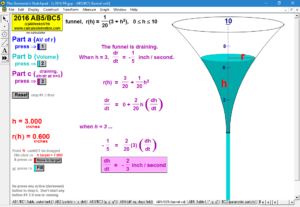
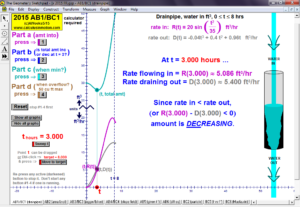
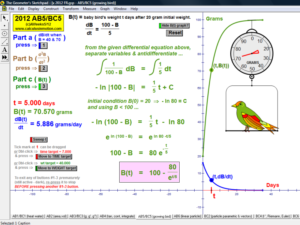
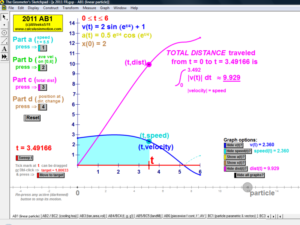
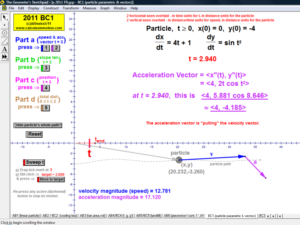
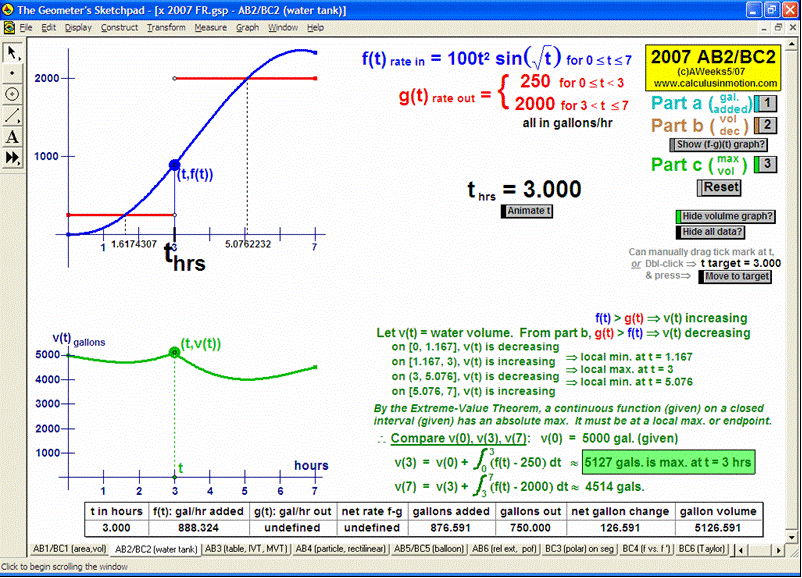
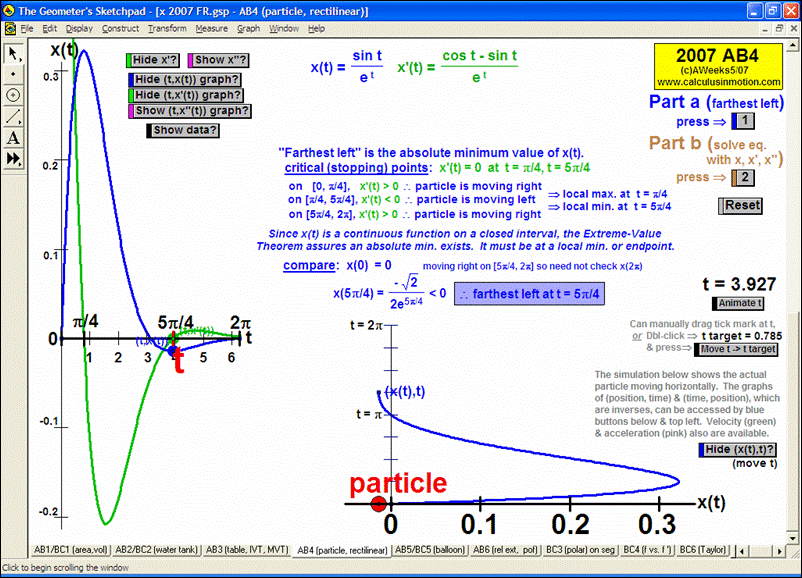
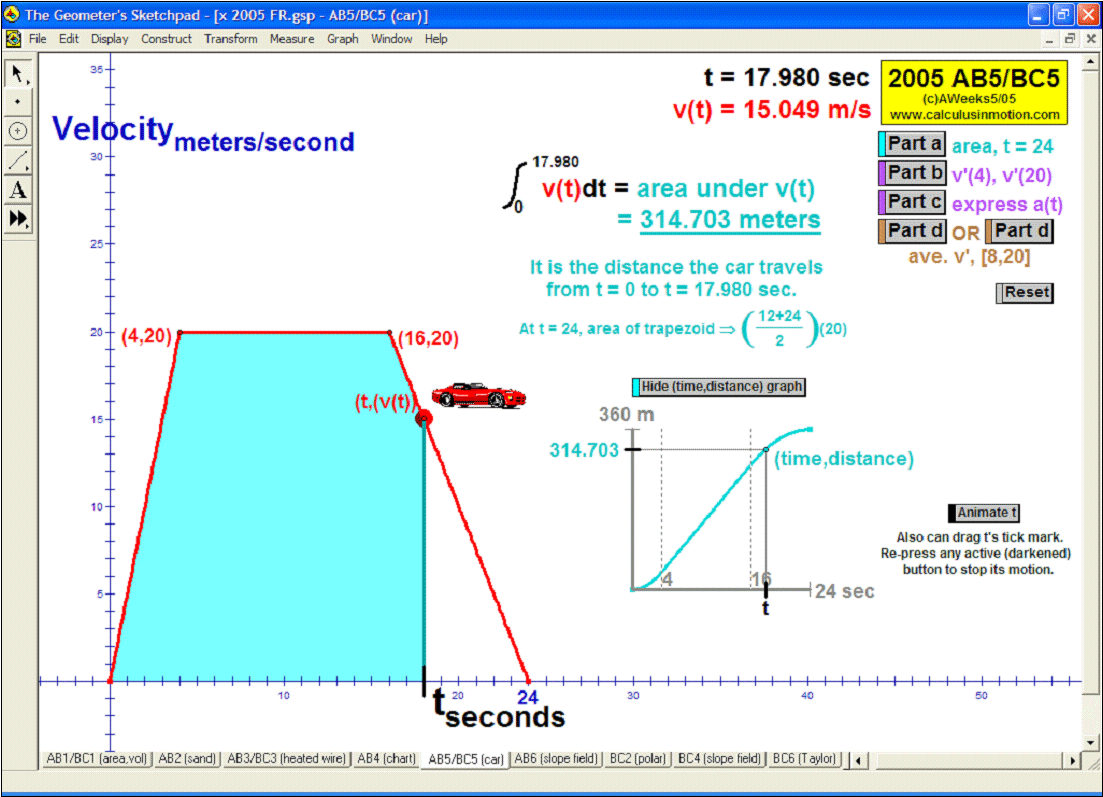
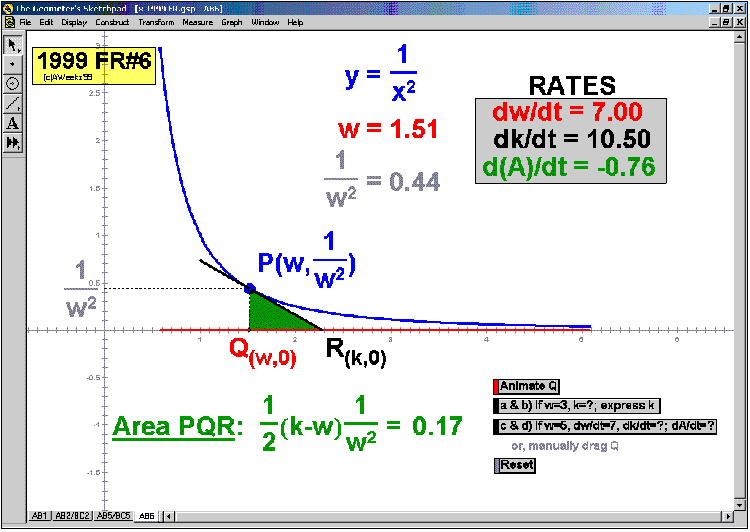
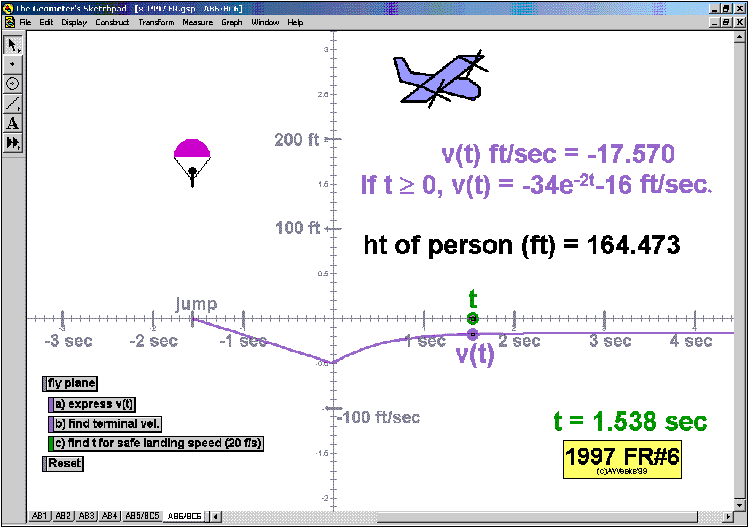
RELATED RATES
A click of a button advances time to commence the action to these classic problems.
Other buttons reveal the values and graphs of the rates.
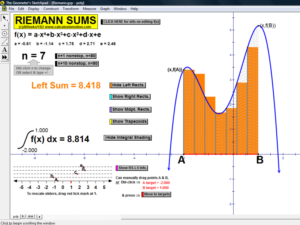
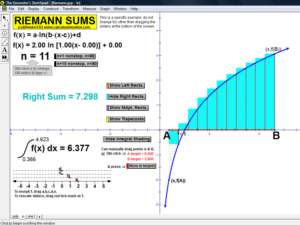
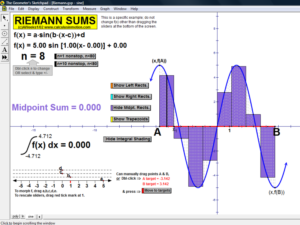
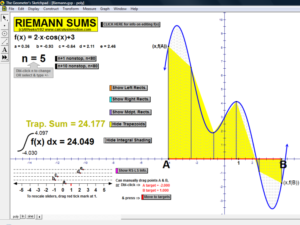
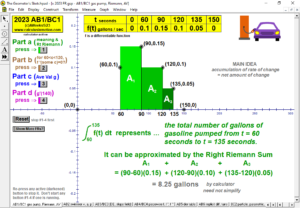
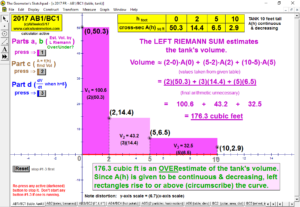
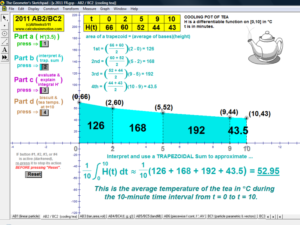
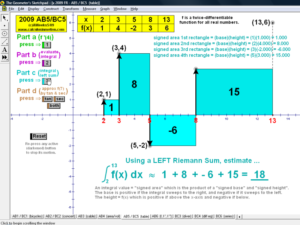
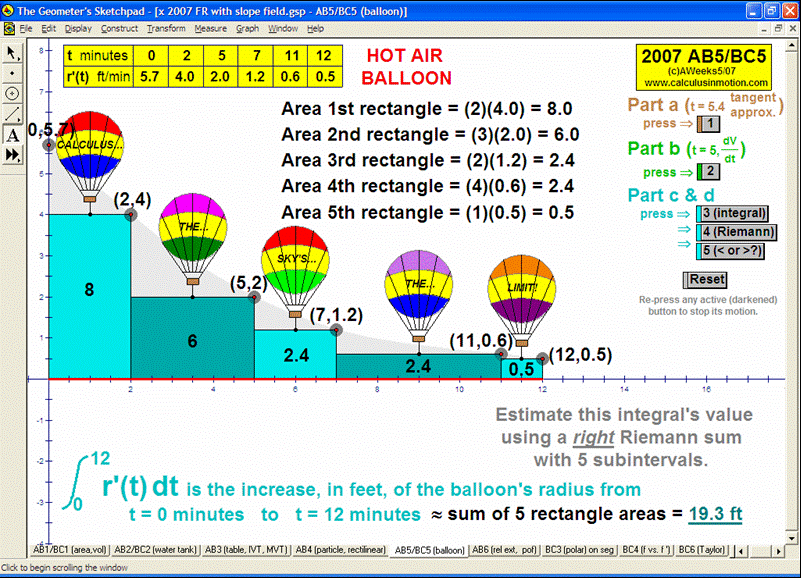
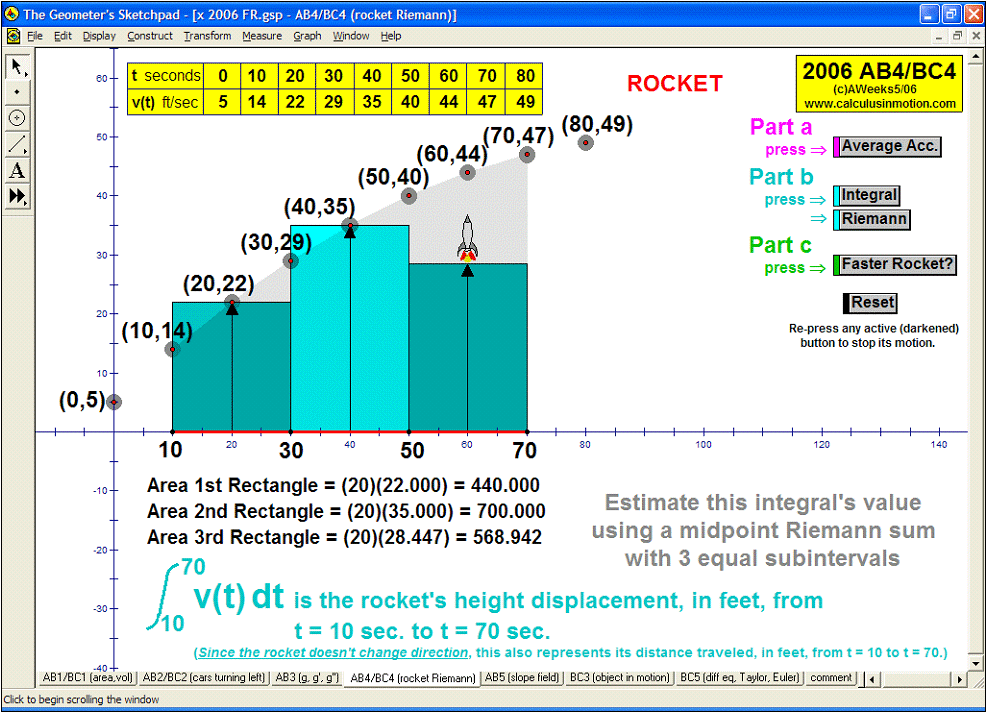
RIEMANN SUMS
Choose rectangles using left endpoints, right endpoints, or midpoints; or trapezoids to approximate an integral for any number
partitions from 1 to 80! Functions can be morphed by dragging sliders, or use the first page to type in any desired function for f(x).
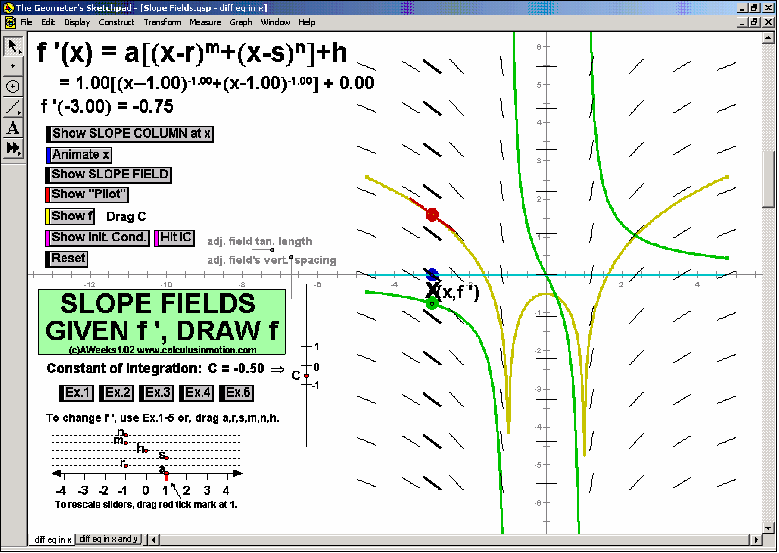
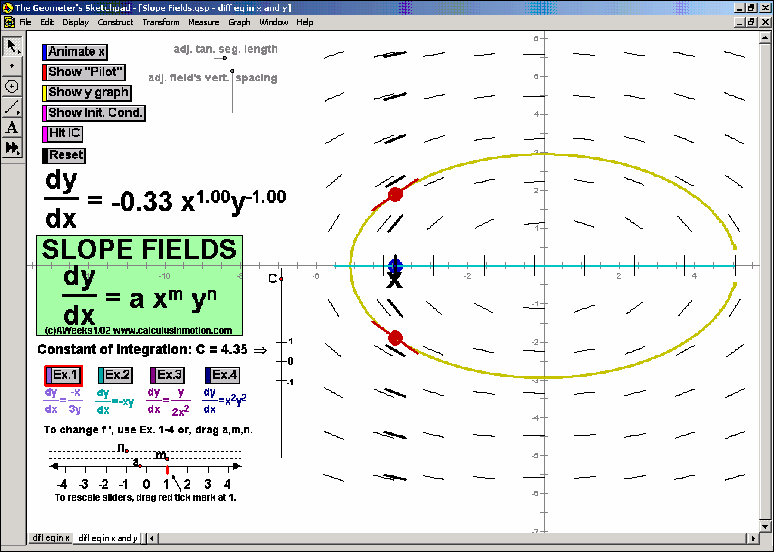
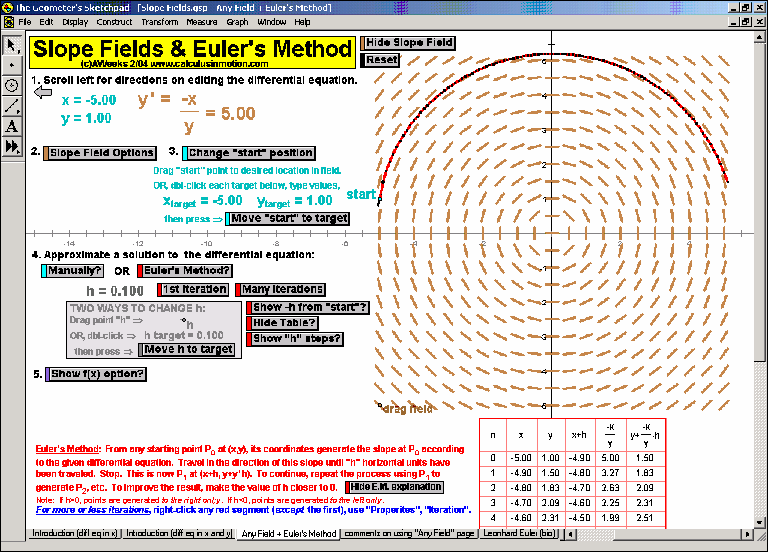
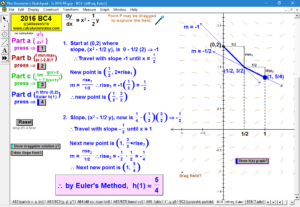
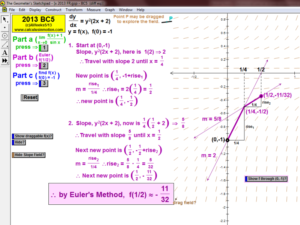
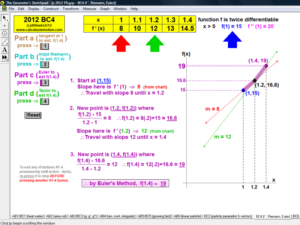
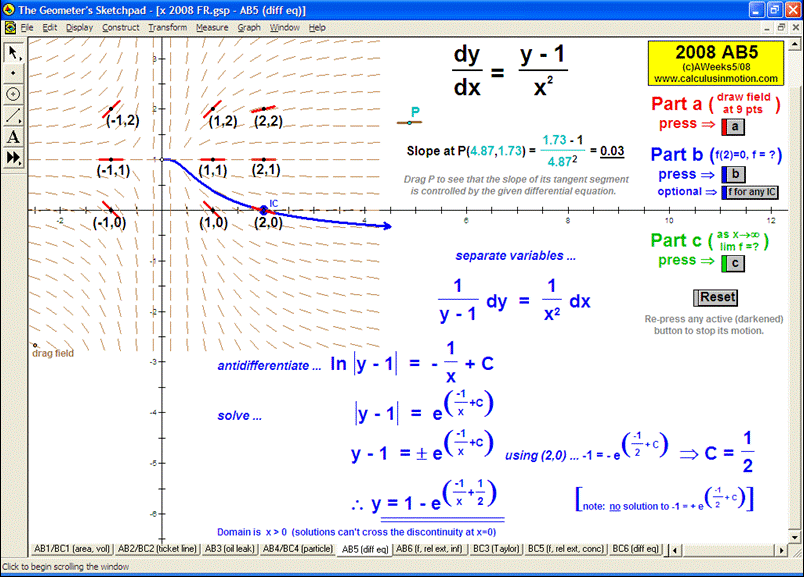
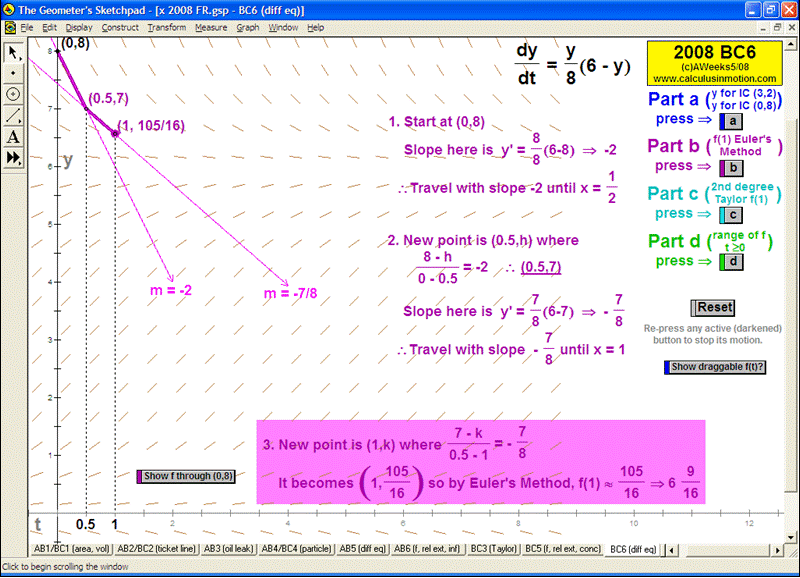
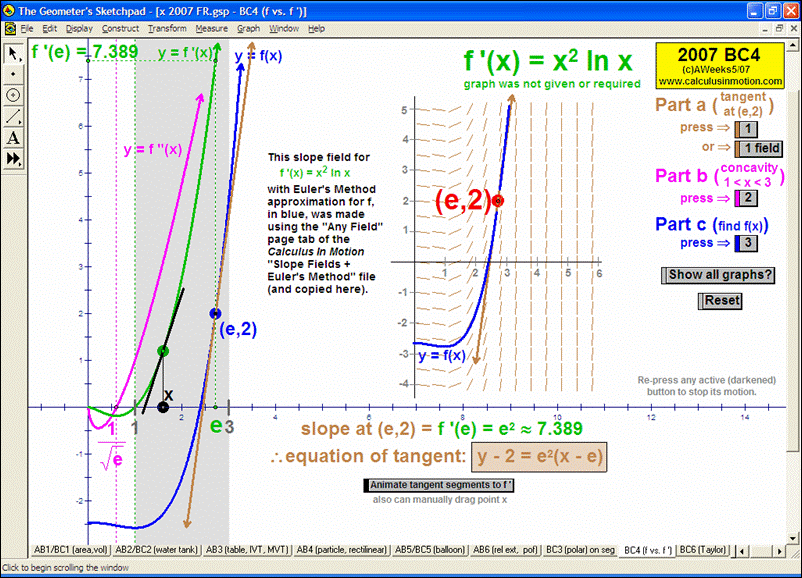
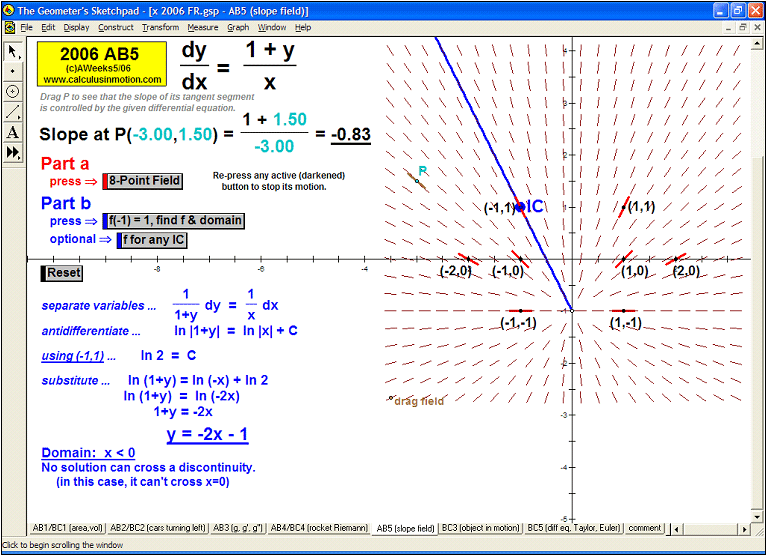
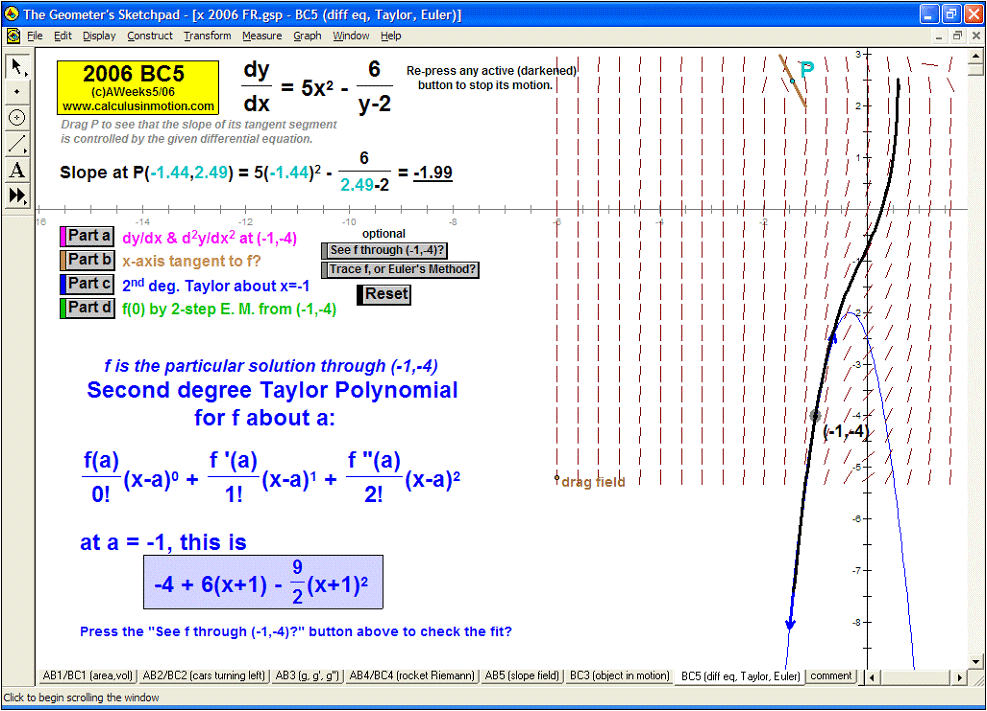
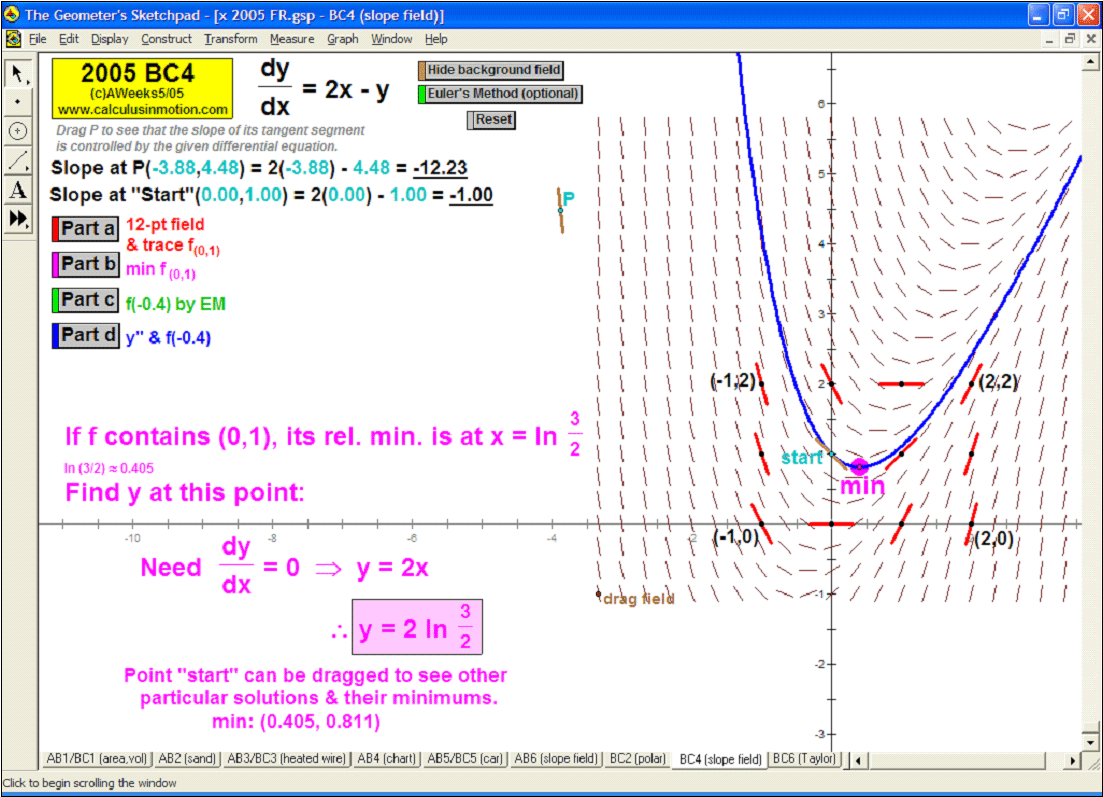
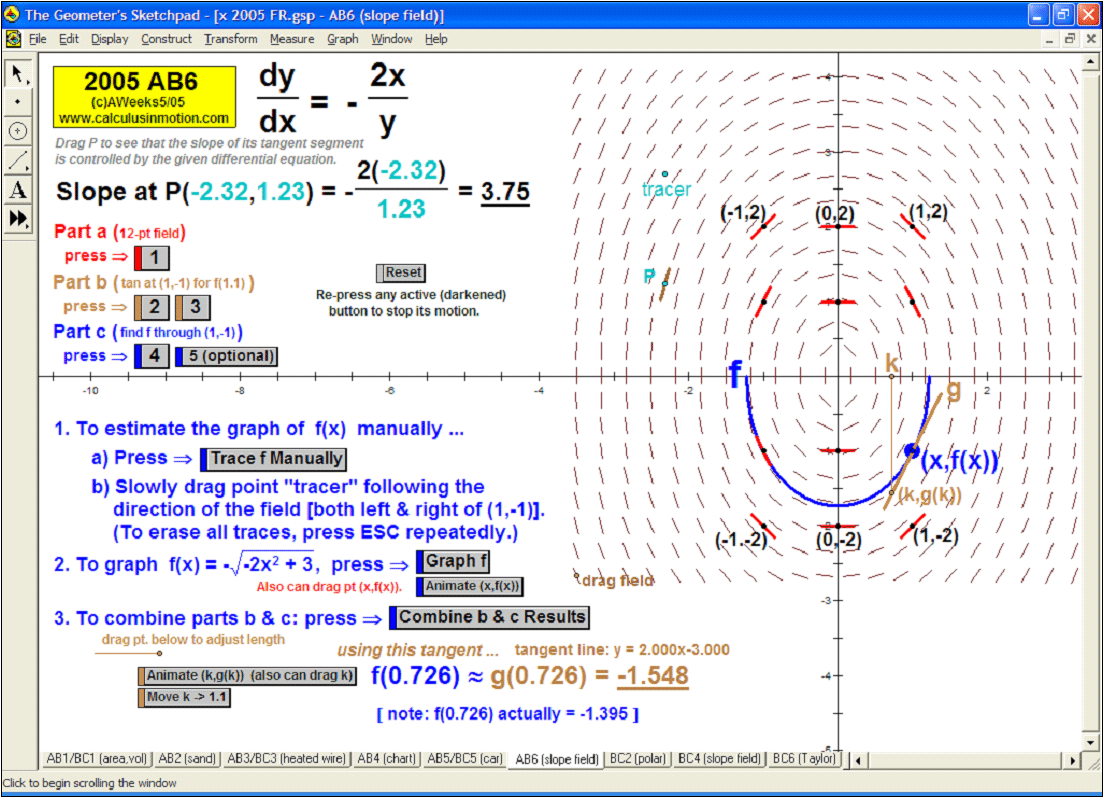
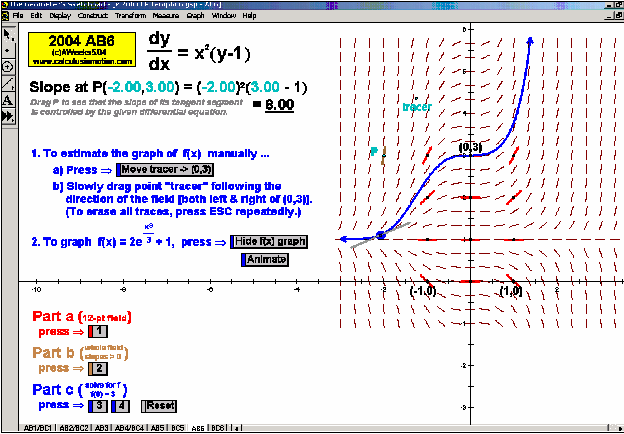
SLOPE FIELDS & EULER’S METHOD
To introduce what a slope field is, use the graph of f ’ to see its values controlling a gliding dynamic “slope column”.
Snapshots of this column are the slope field. A tangent segment “pilots” the field to draw f.
Once understood, a different animation allows any differential equation to be entered and generates the slope field.
Manually follow the field to draw f or use Euler’s Method (includes explanation of E.M. and numerical table of data). Easily adjustable.
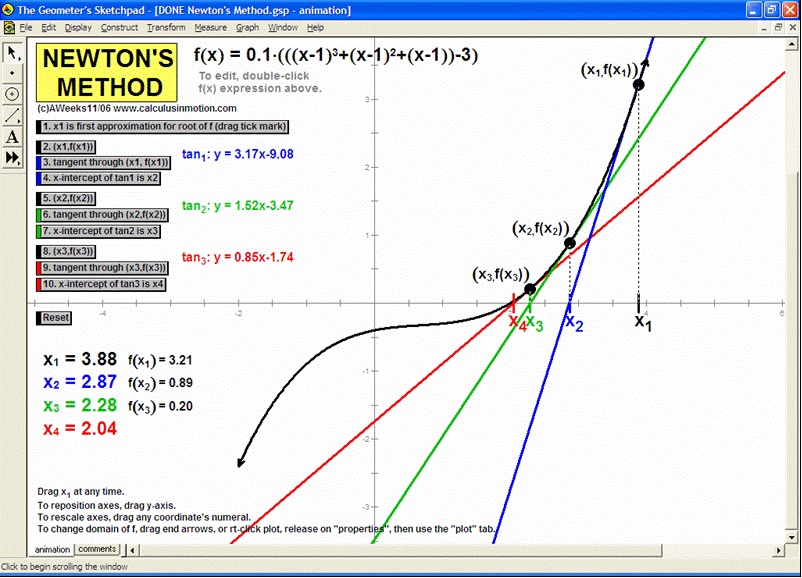
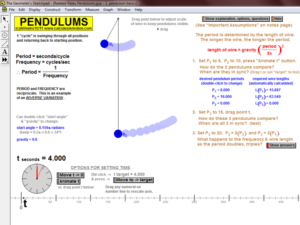
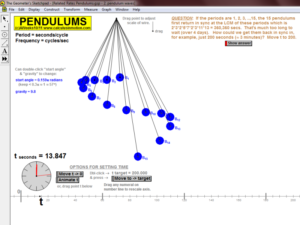
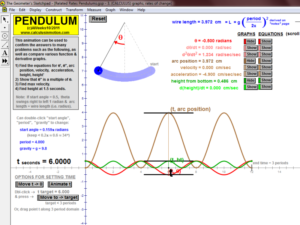
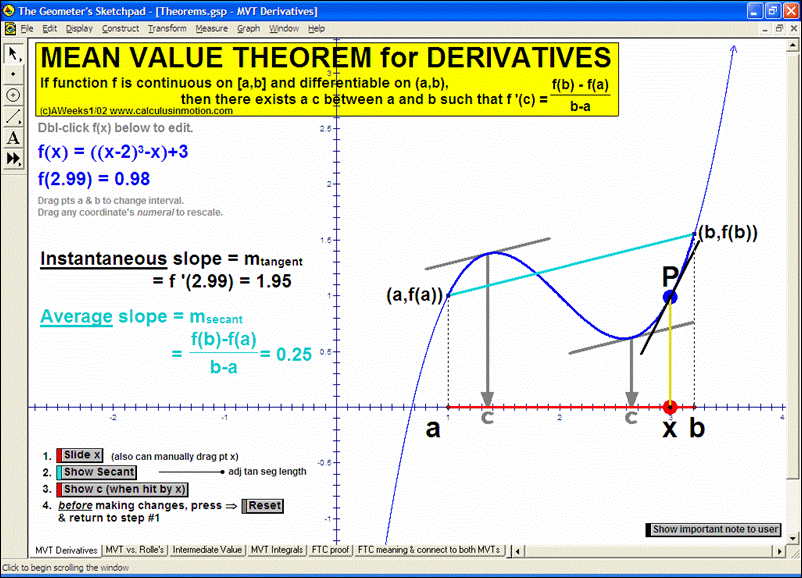
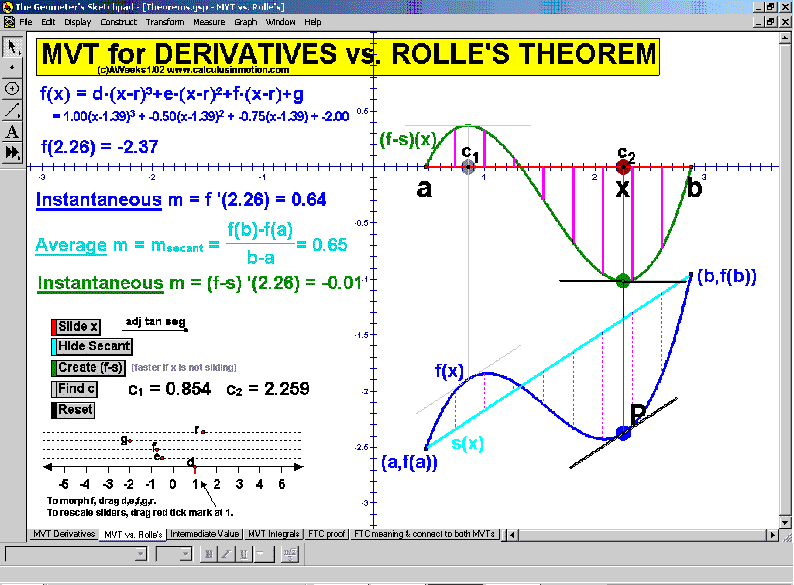
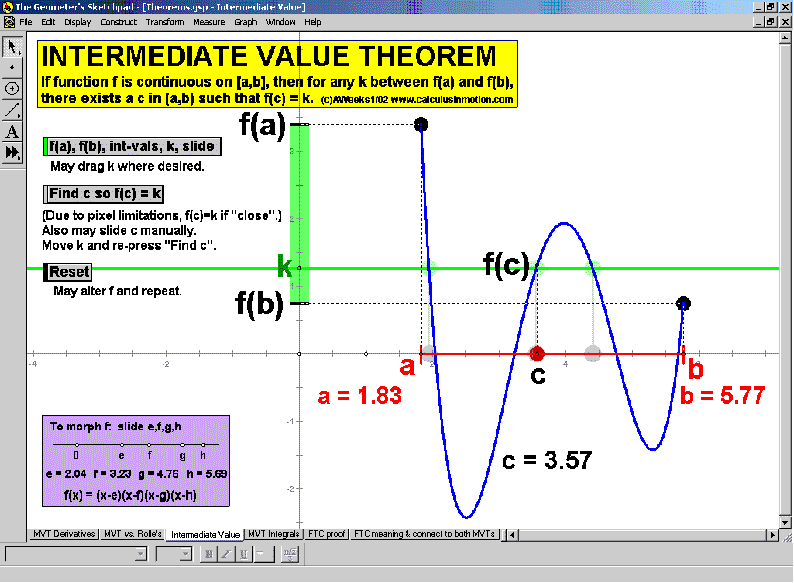
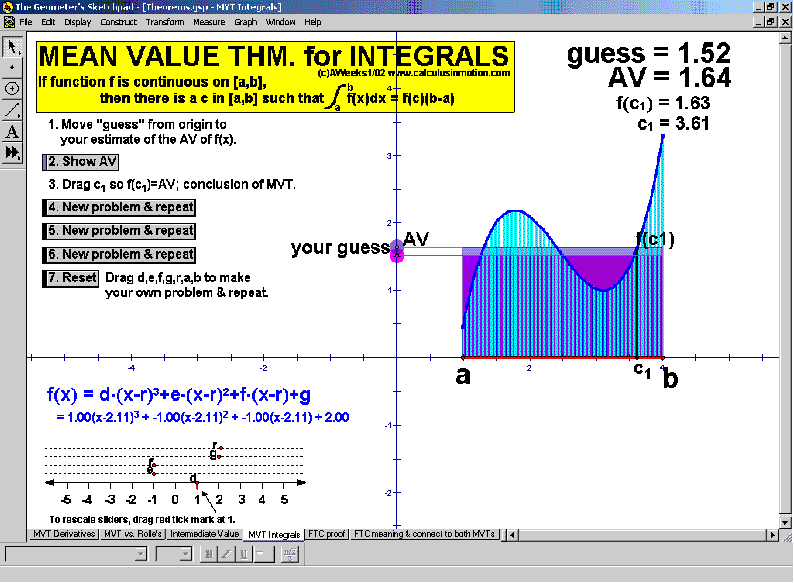
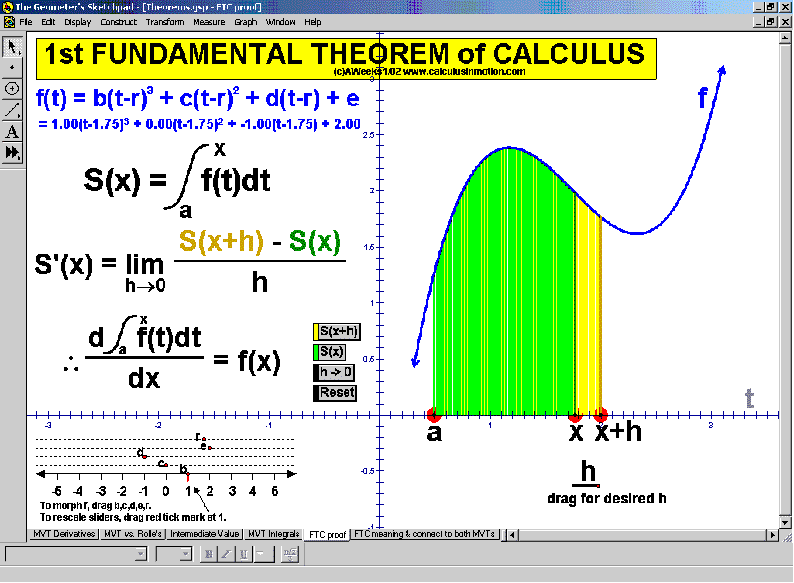
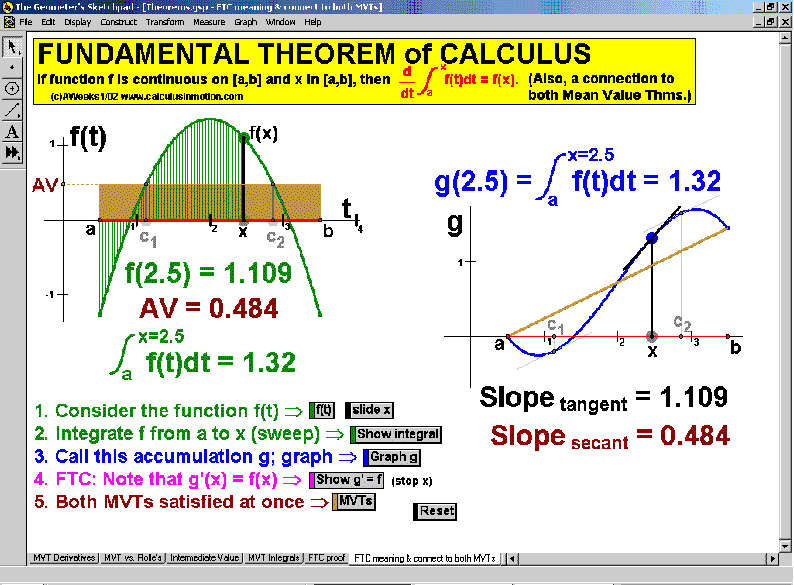
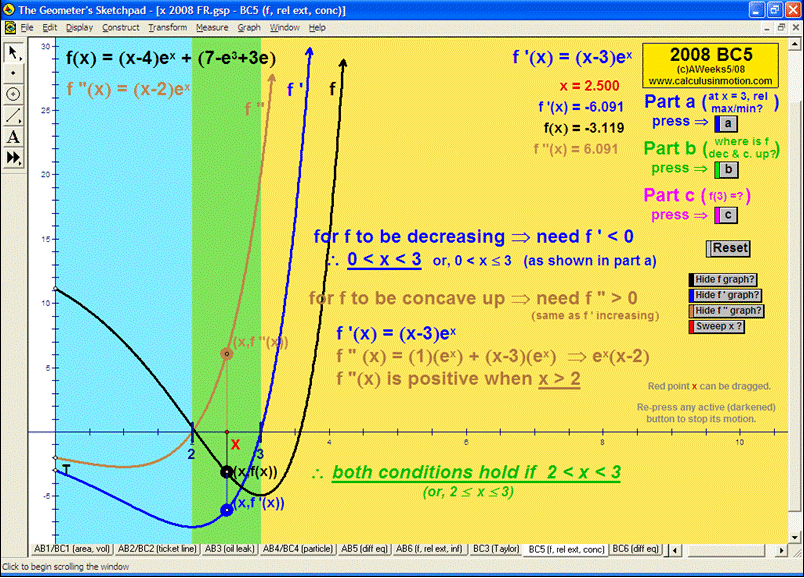
THEOREMS
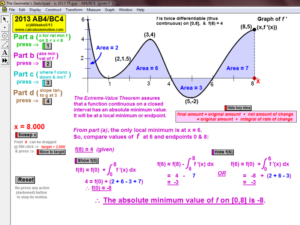
Mean-Value Theorem for Derivatives, Mean-Value Thm. for Derivatives vs. Rolle’s Thm., Intermediate-Value Theorem
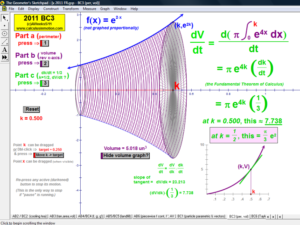
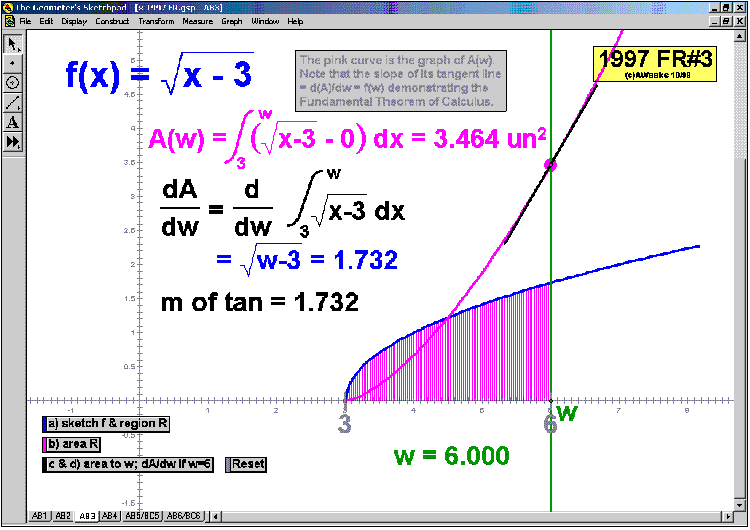
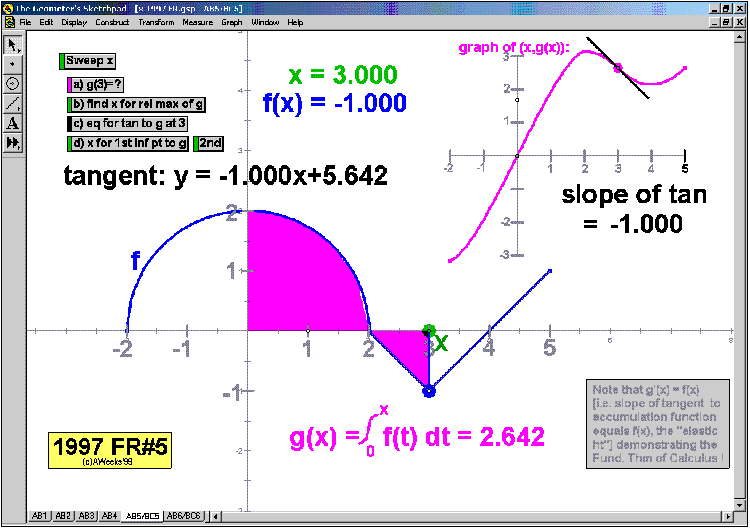
Mean-Value Theorem for Integrals (a little game),1st Fundamental Theorem of Calculus (a visual proof)
Connect the 1st FTC to both Mean-Value Theorems
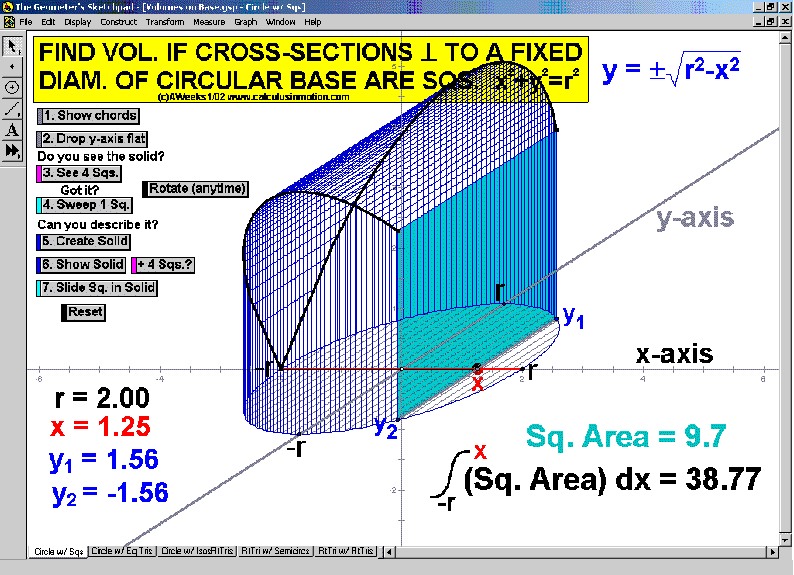
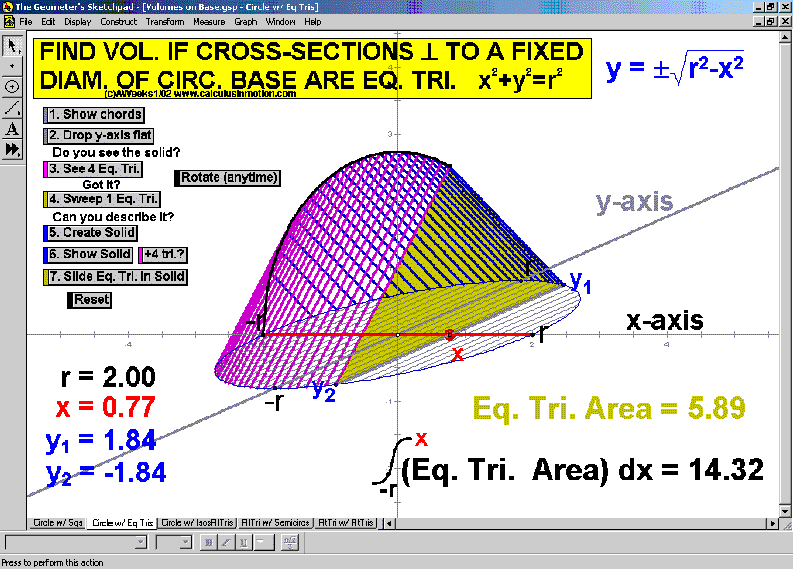
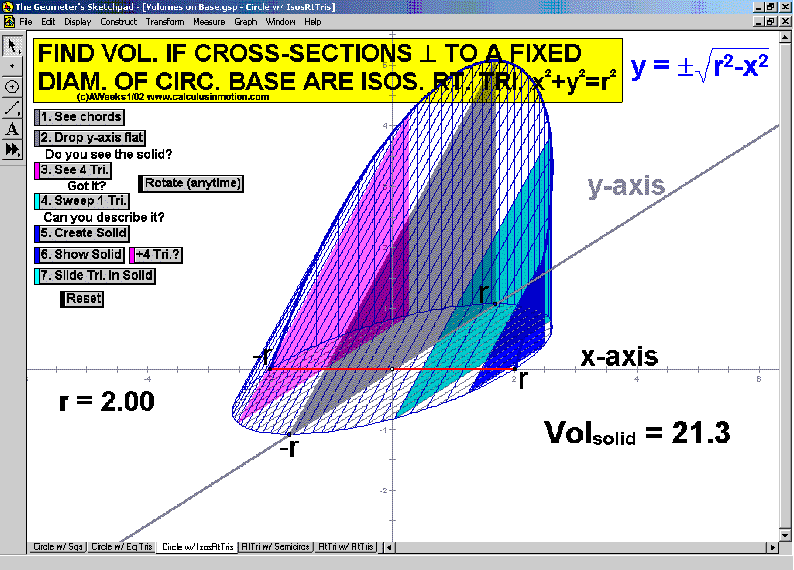
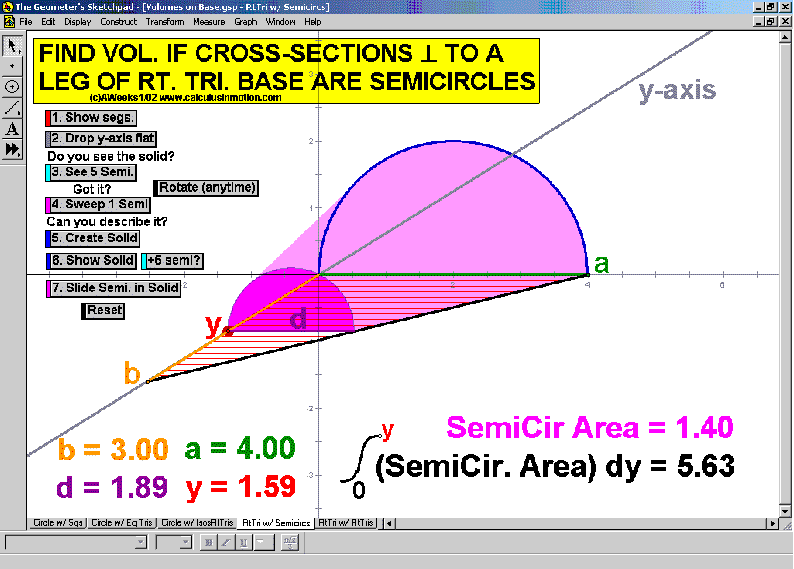
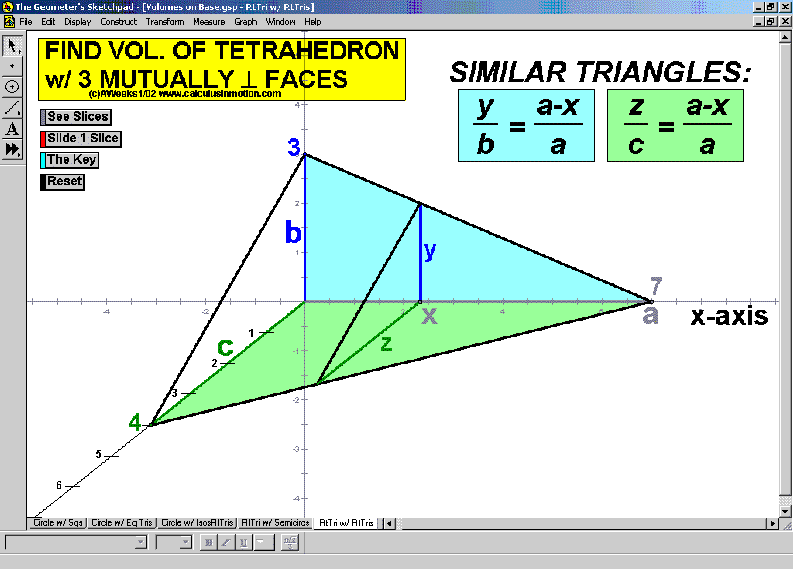
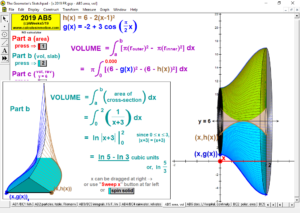
VOLUMES ON A BASE
Visualize these shapes one step at a time. Start by rotating the xy-plane to horizontal.
View a few stationary slices, then a sweeping slice, and finally, an accumulating slice.
Rotate the solid any time for other viewing angles. Choose from an assortment of bases and cross-sections.
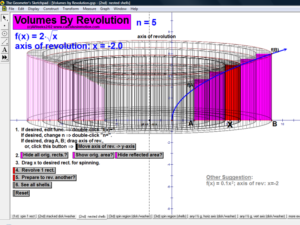
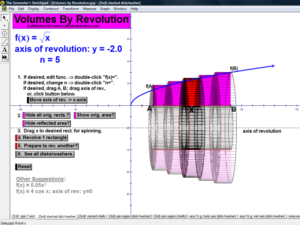
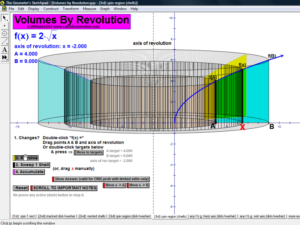
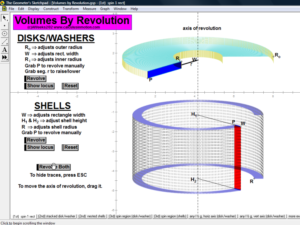
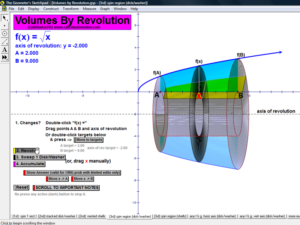
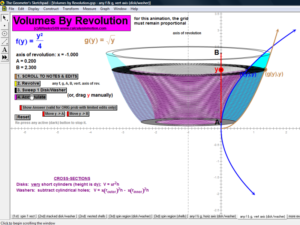
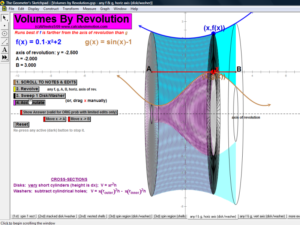
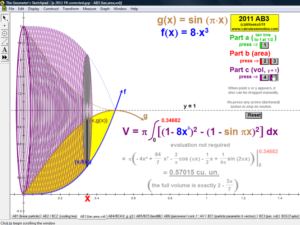
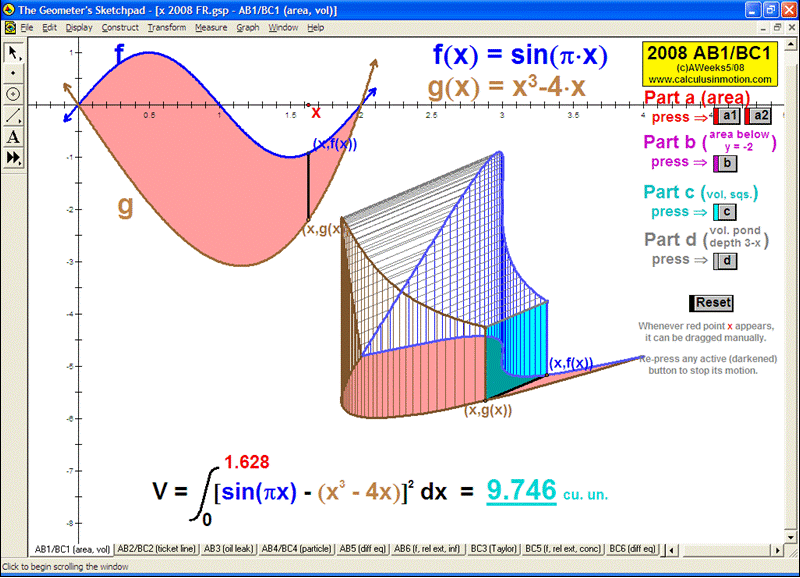
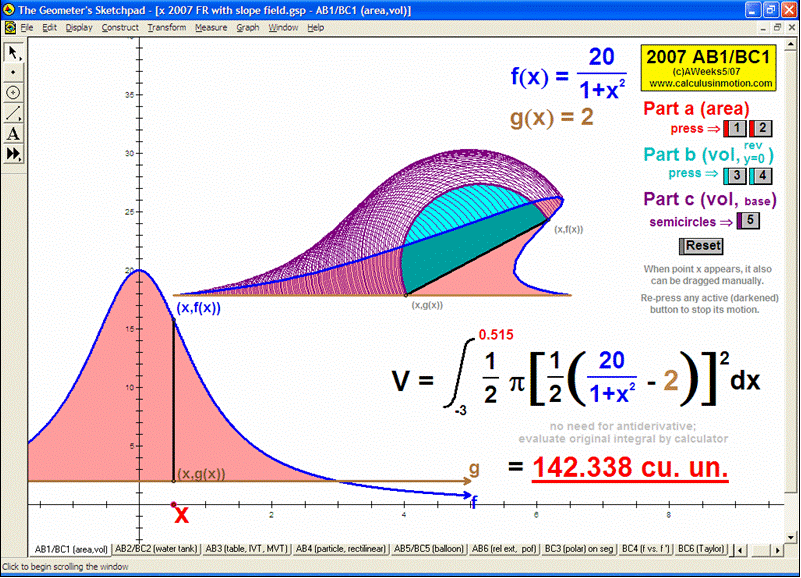
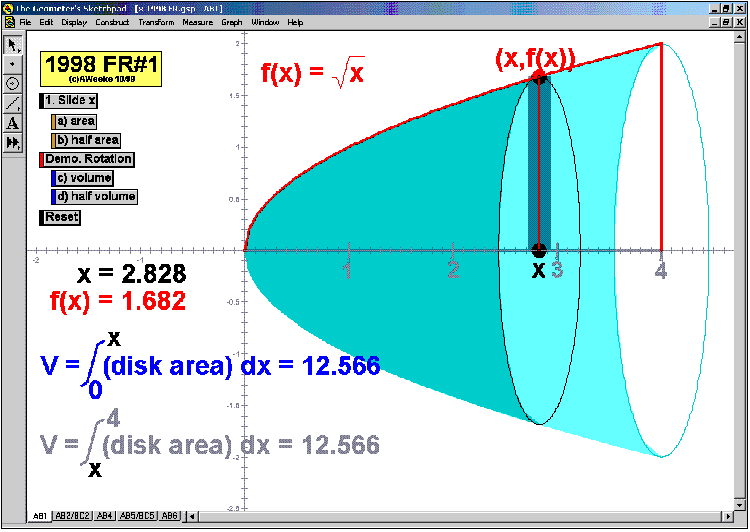
VOLUMES BY REVOLUTION
These animations cover both the disk/washer technique and the cylindrical shell technique.
Develop the process by first revolving one lone rectangle. Next, revolve several rectangles in a region and stack or nest the results.
Finally, revolve any desired region (bounded by 1 or 2 functions of choice) on an interval of choice, about any horizontal or vertical axis.
—-
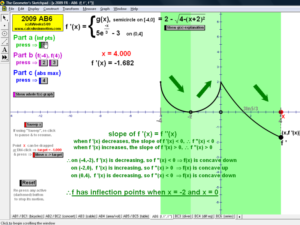
205 ANIMATIONS OF AP CALCULUS AB & BC EXAMS’
RELEASED FREE RESPONSE QUESTIONS 2023 – 1997
Click below to link to AP Central for statements of the Free Response
Questions from the exams for …
AP CALCULUS *AB* 2023 and earlier
AP CALCULUS * BC* 2023 and earlier
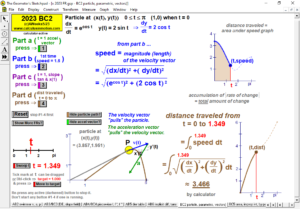
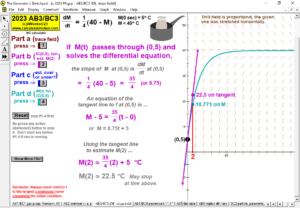
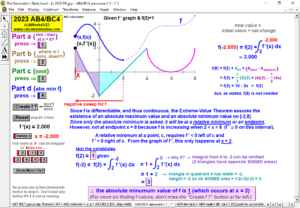
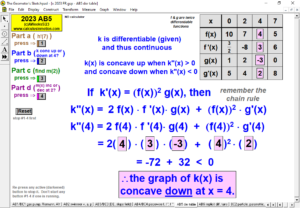
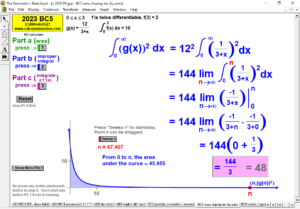
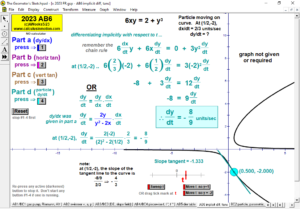
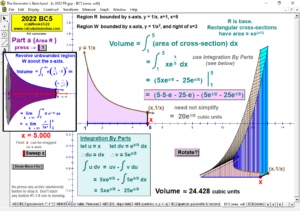
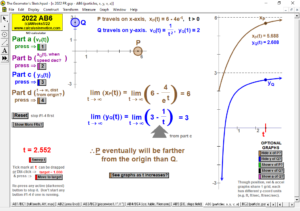
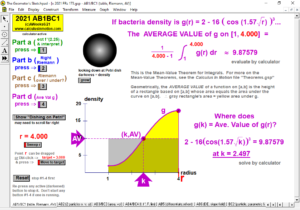
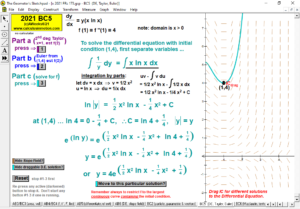
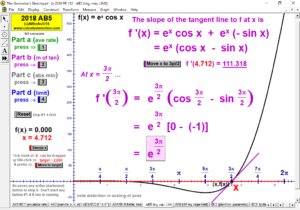
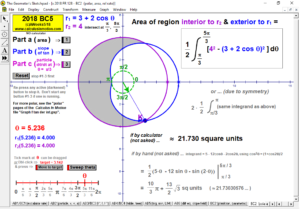
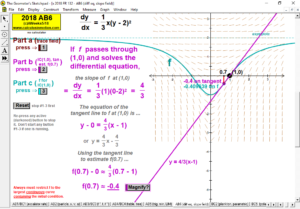
2023 animations to AP Calculus AB/BC Exams’ FRs
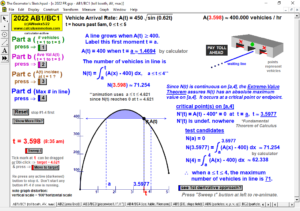
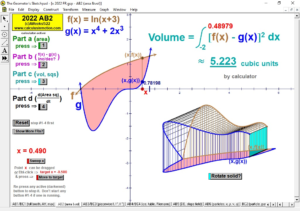
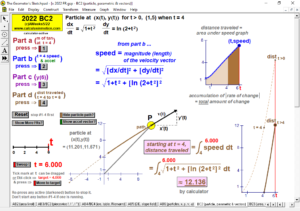
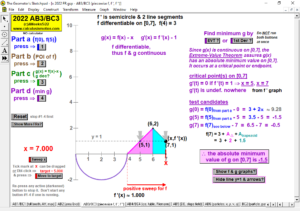
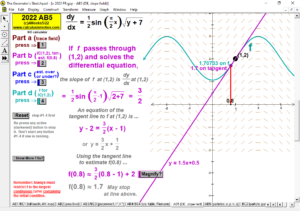
2022 animations to AP Calculus AB/BC Exams’ FRs
2021 animations to AP Calculus AB/BC Exams’ FRs
2020: due to Covid-19 changes, the College Board did not publicly release any AP Calculus exam questions
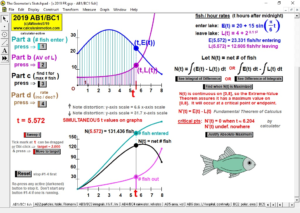
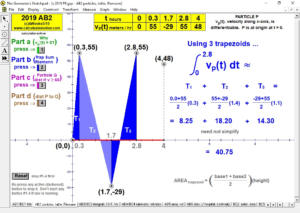
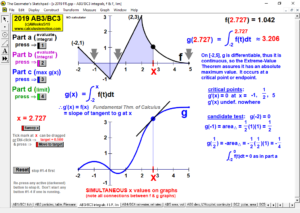
2019 animations to AP Calculus AB/BC Exams’ FRs
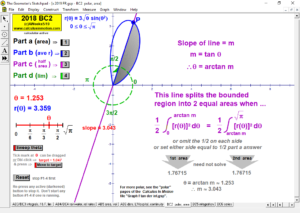
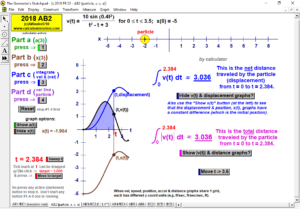
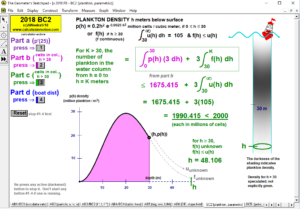
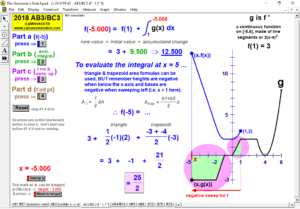
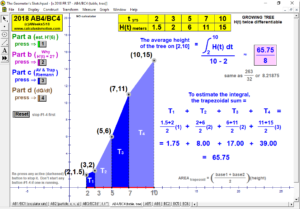
2018 animations to AP Calculus AB/BC Exams’ FRs
2017 animations to AP Calculus AB/BC Exams’ FRs
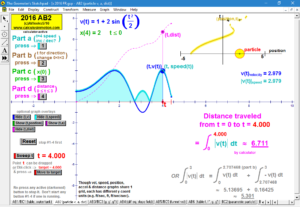
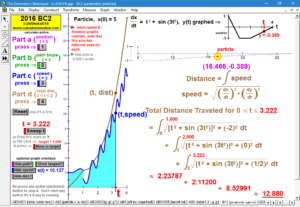
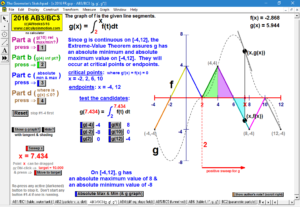
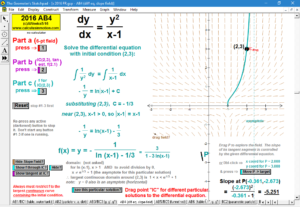
2016 animations to AP Calculus AB/BC Exams’ FRs
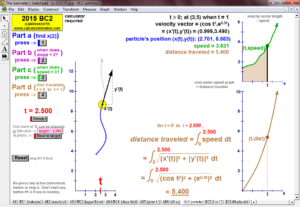
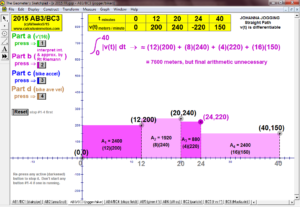
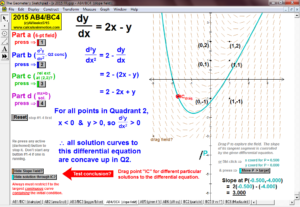
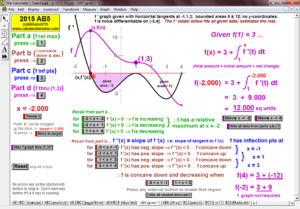
2015 animations to AP Calculus AB/BC Exams’ FRs
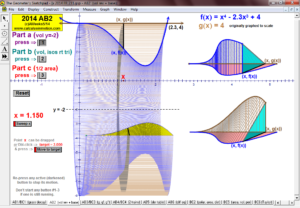
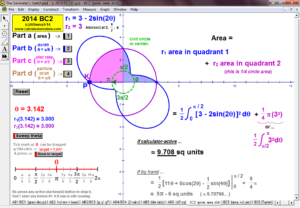
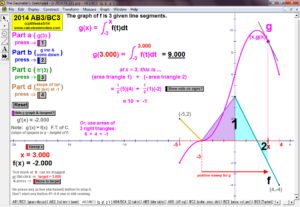
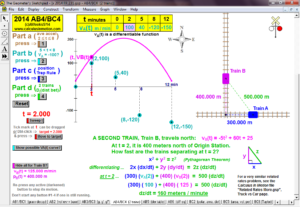
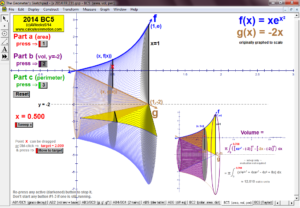
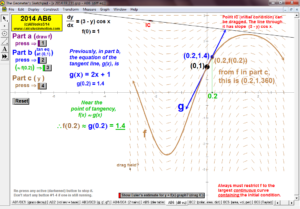
2014 animations to AP Calculus AB/BC Exams’ FRs
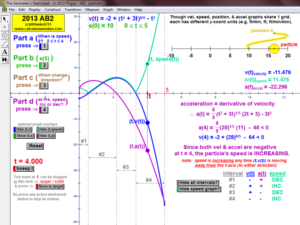
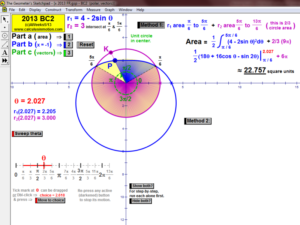
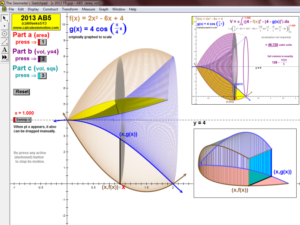
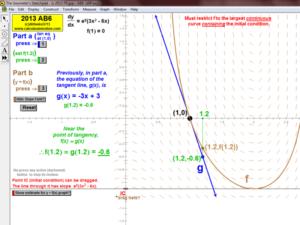
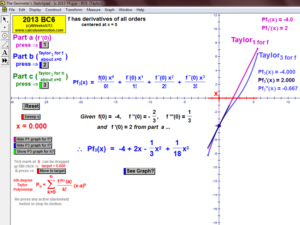
2013 animations to AP Calculus AB/BC Exams’ FRs
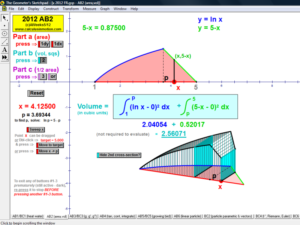
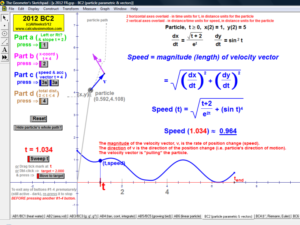
2012 animations to AP Calculus AB/BC Exams’ FRs
2011 animations to AP Calculus AB/BC Exams’ FRs
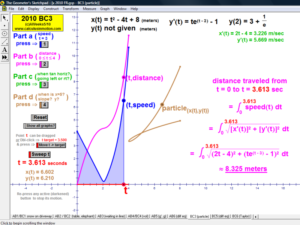
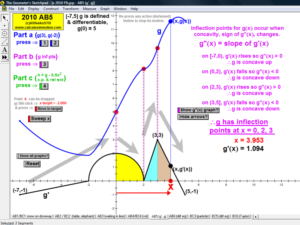
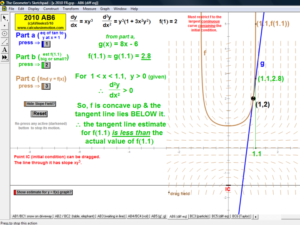
2010 animations to AP Calculus AB/BC Exams’ FRs
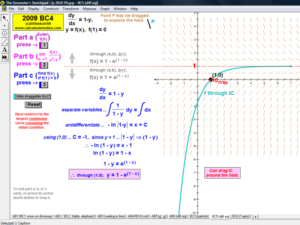
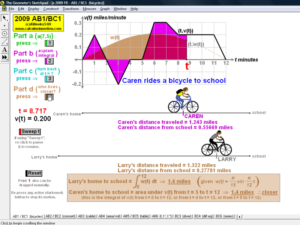
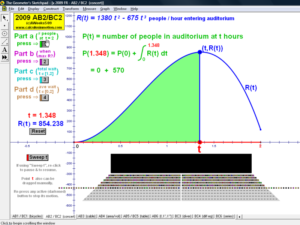
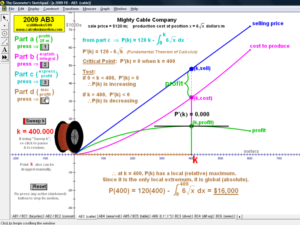
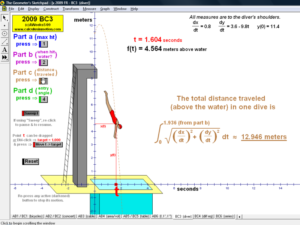
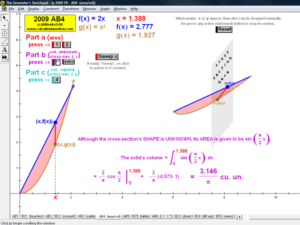
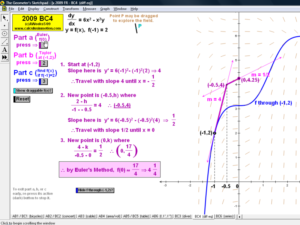
2009 animations to AP Calculus AB/BC Exams’ FRs
2008 animations to AP Calculus AB/BC Exams’ FRs
2007 animations to AP Calculus AB/BC Exams’ FRs
2006 animations to AP Calculus AB/BC Exams’ FRs
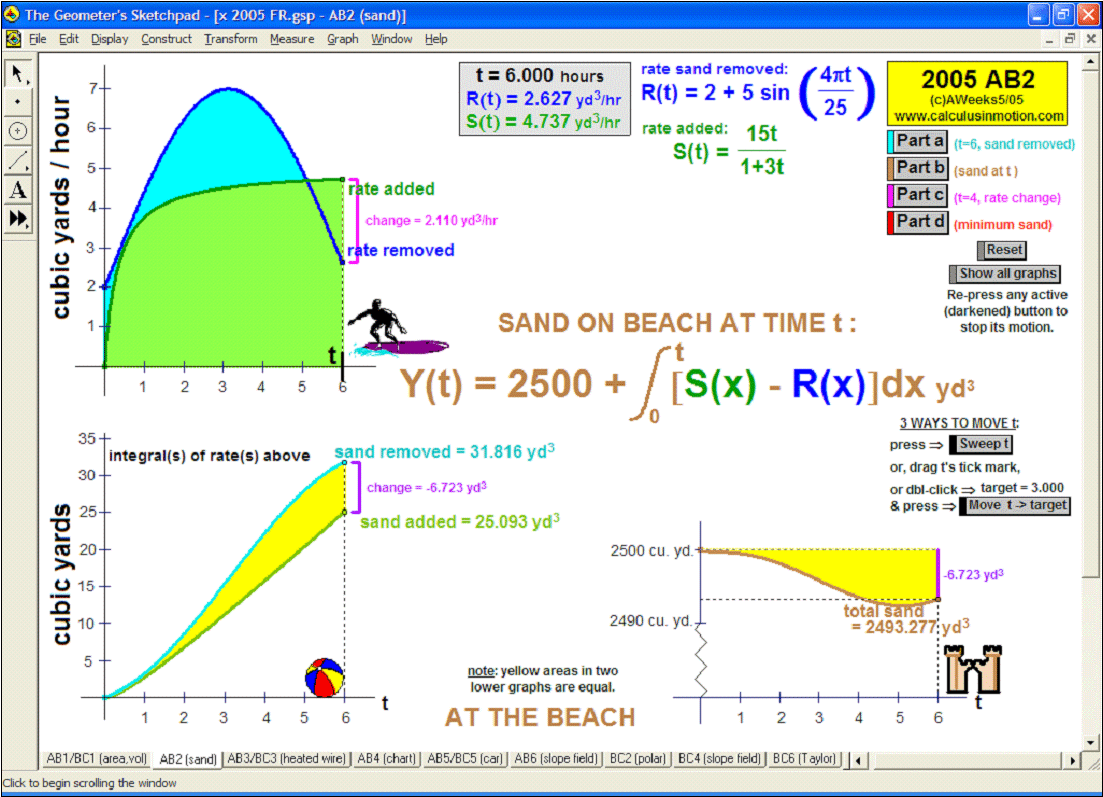
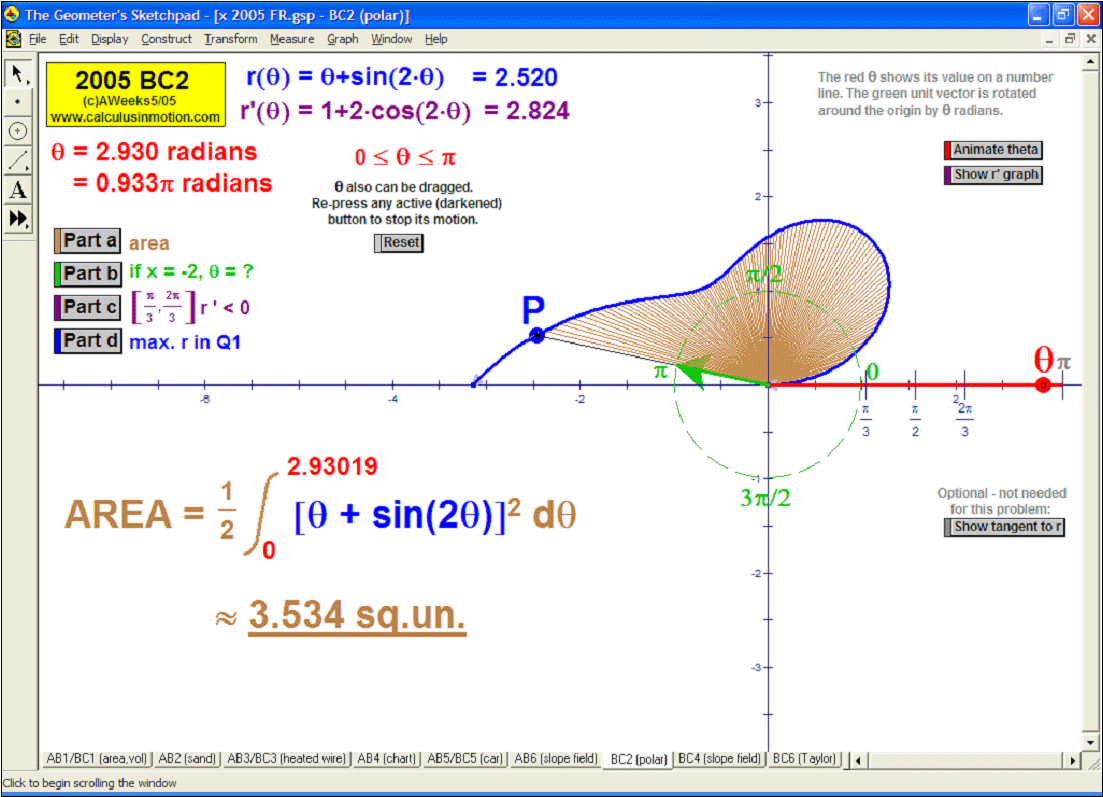
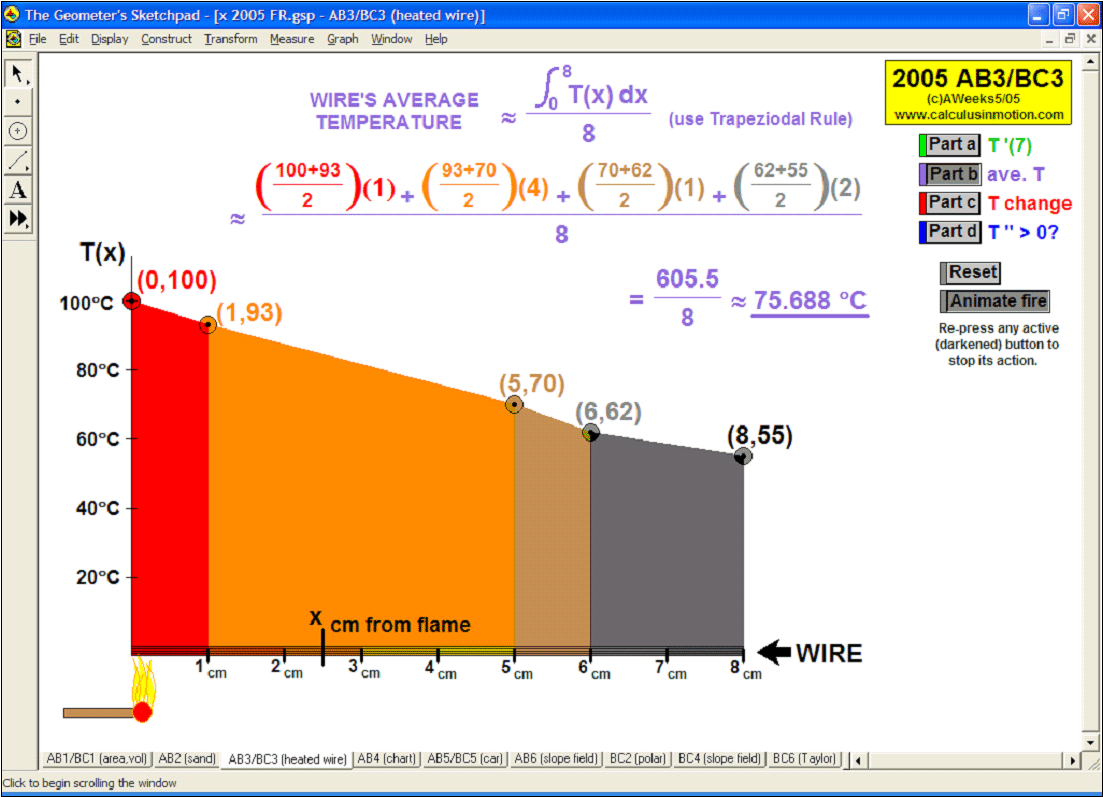
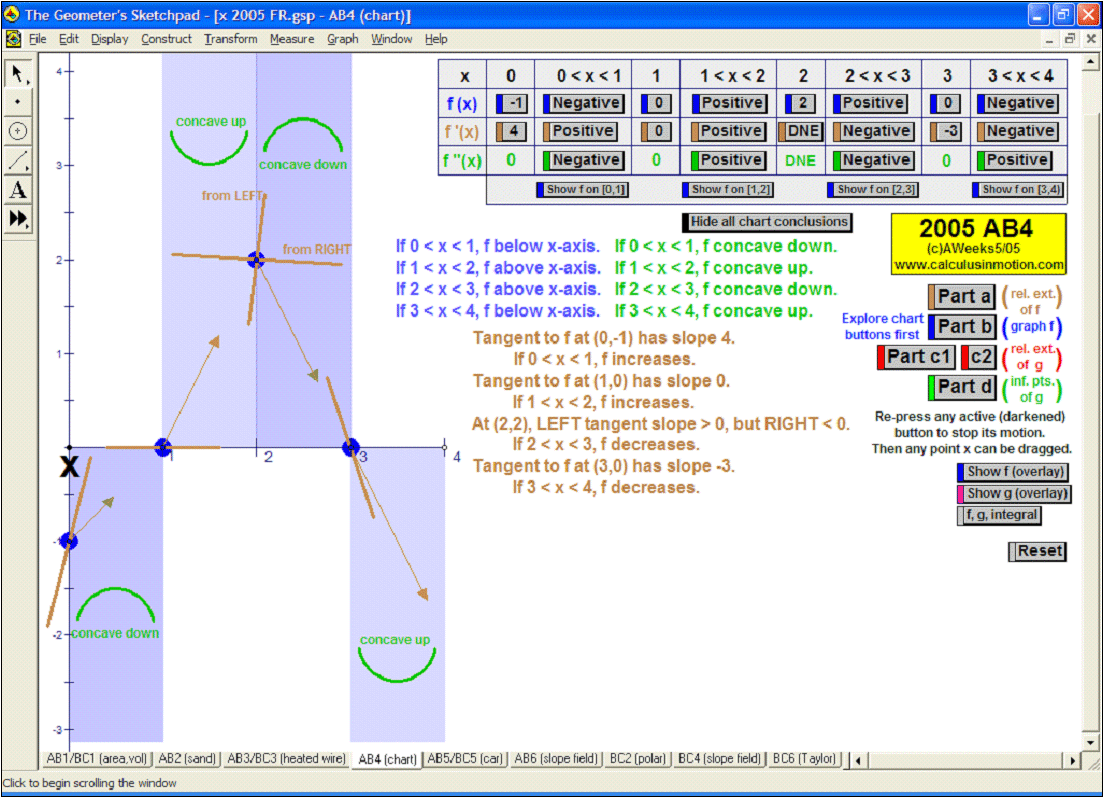
2005 animations to AP Calculus AB/BC Exams’ FRs
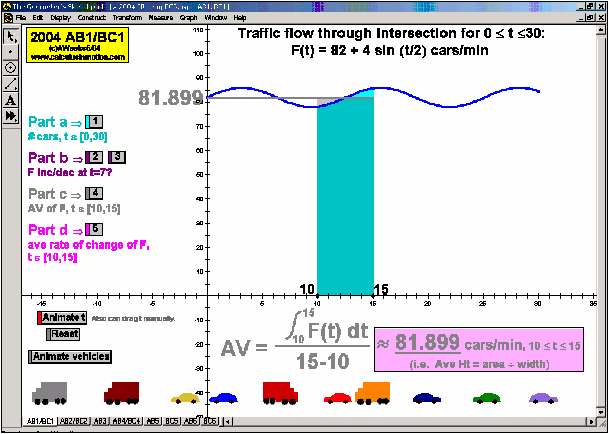
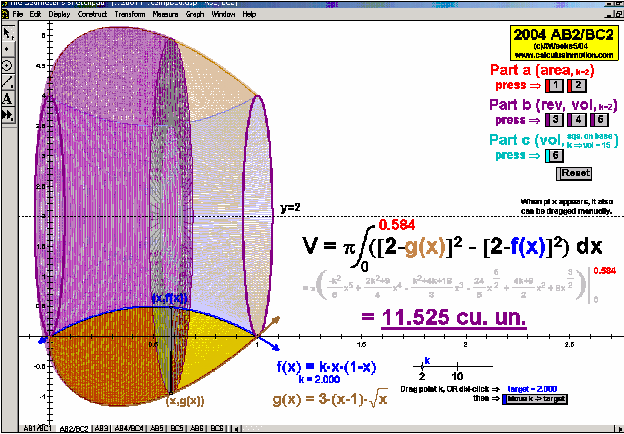
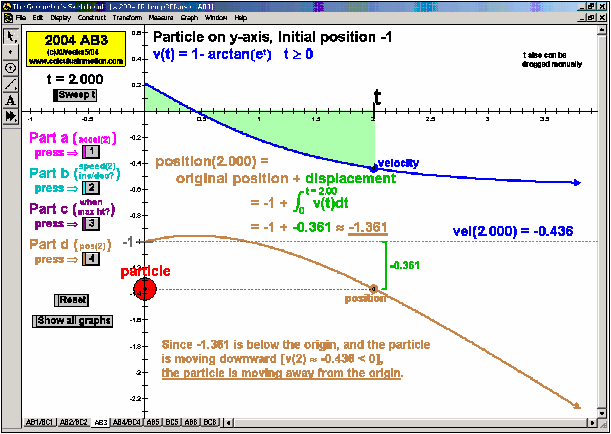
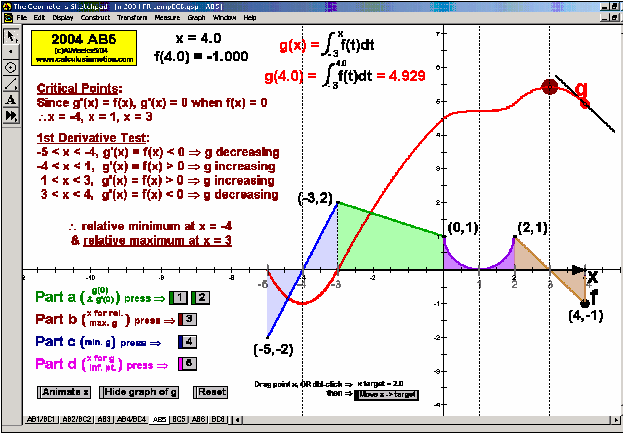
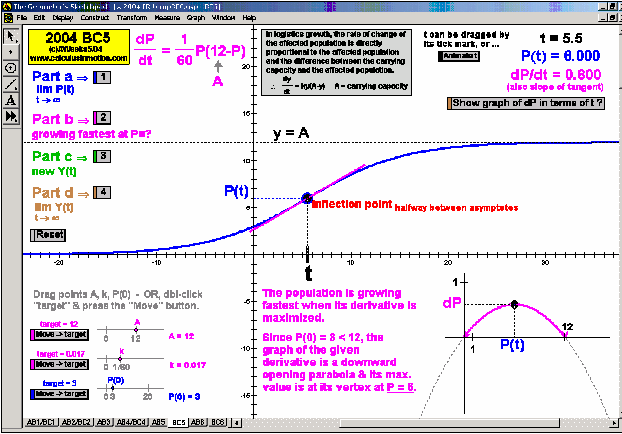
2004 animations to AP Calculus AB/BC Exams’ FRs
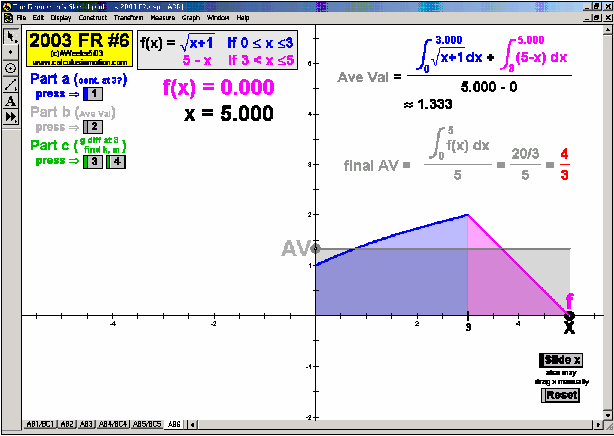
2003 animations to AP Calculus AB/BC Exams’ FRs
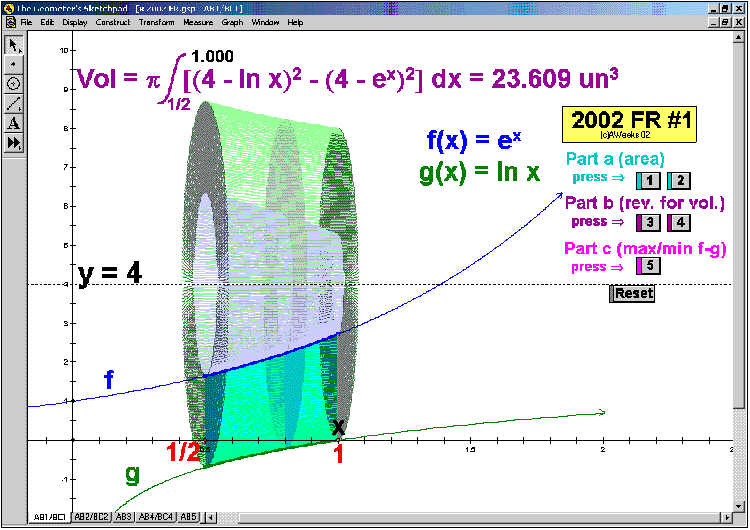
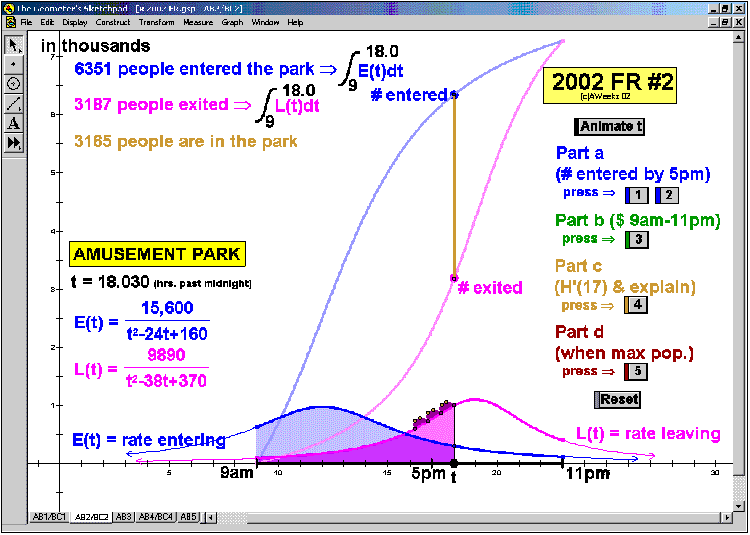
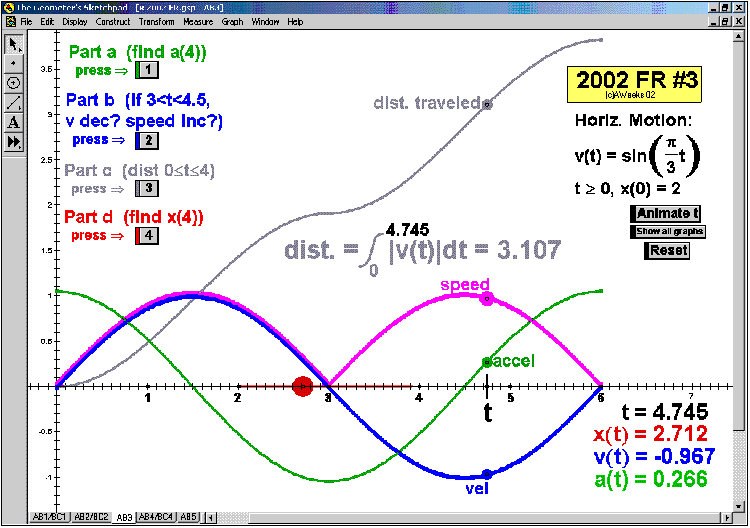
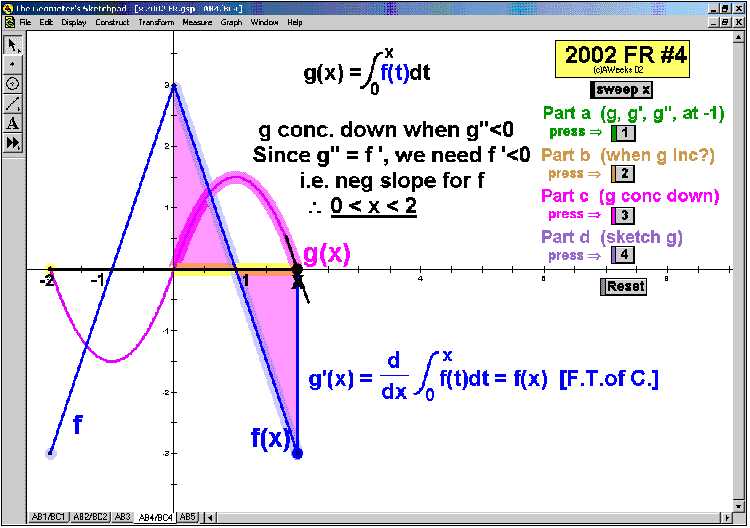
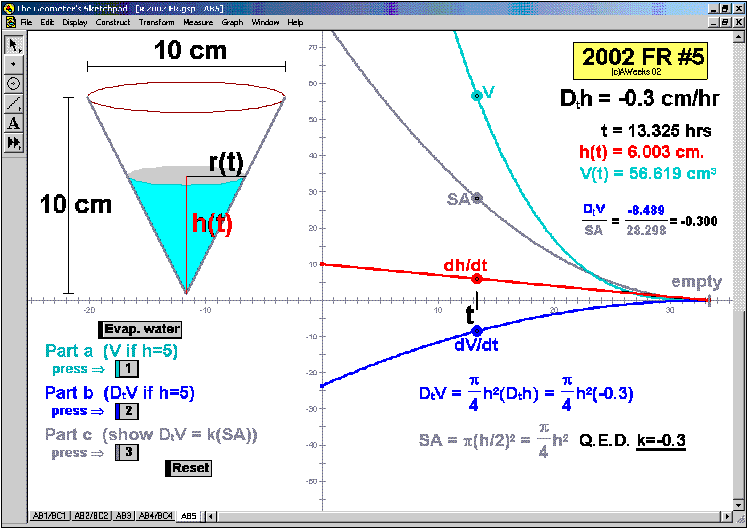
2002 animations to AP Calculus AB/BC Exams’ FRs
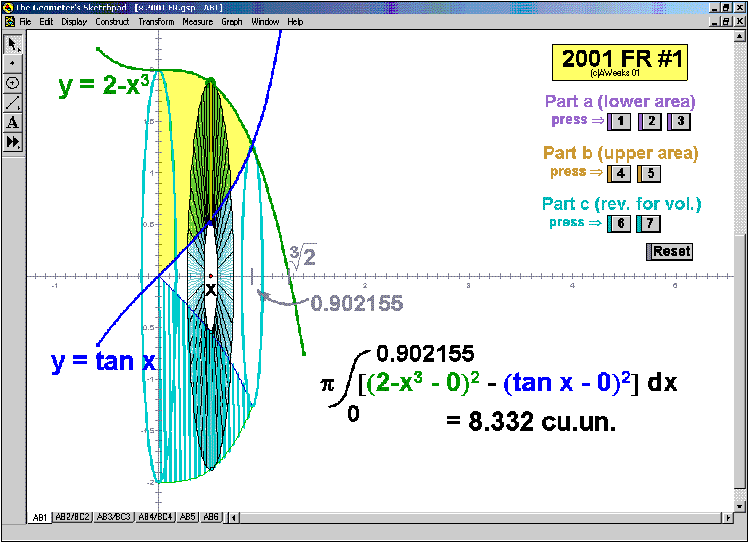
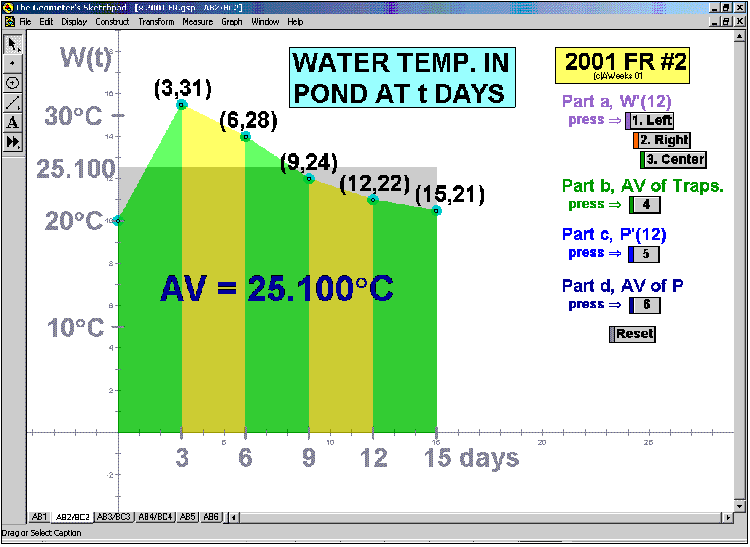
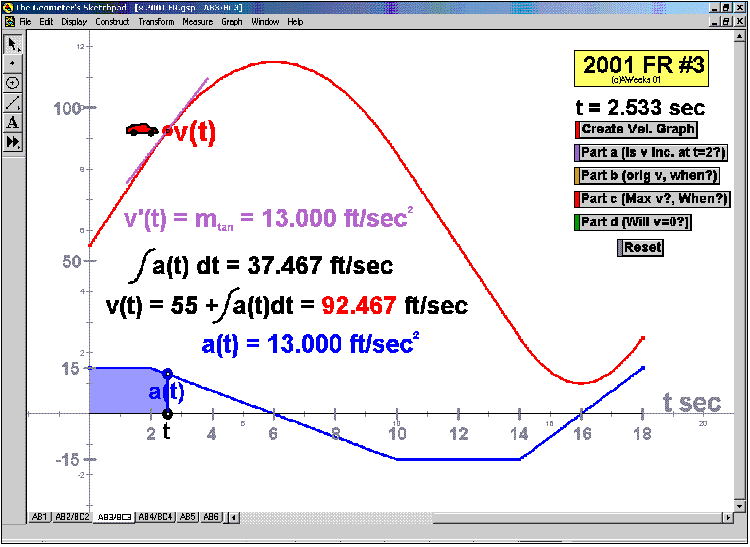
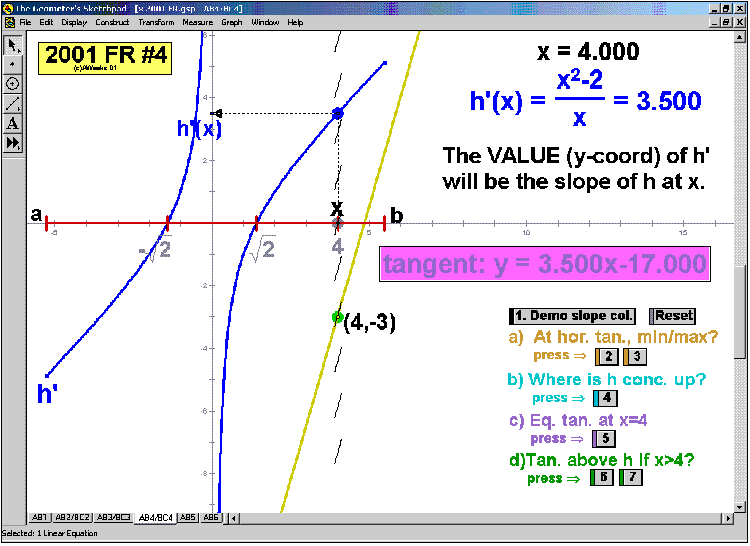
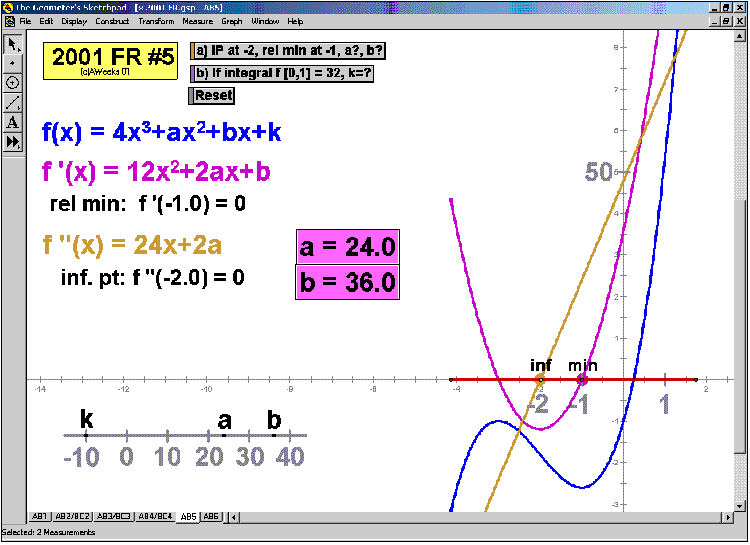
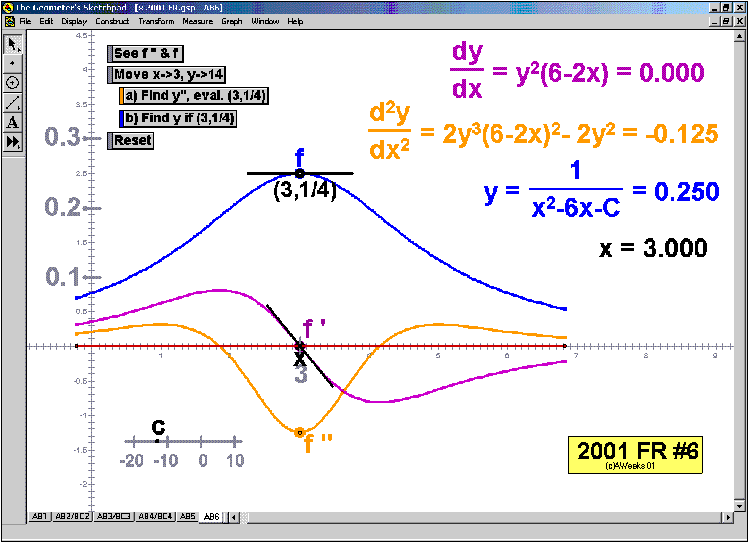
2001 animations to AP Calculus AB/BC Exams’ FRs
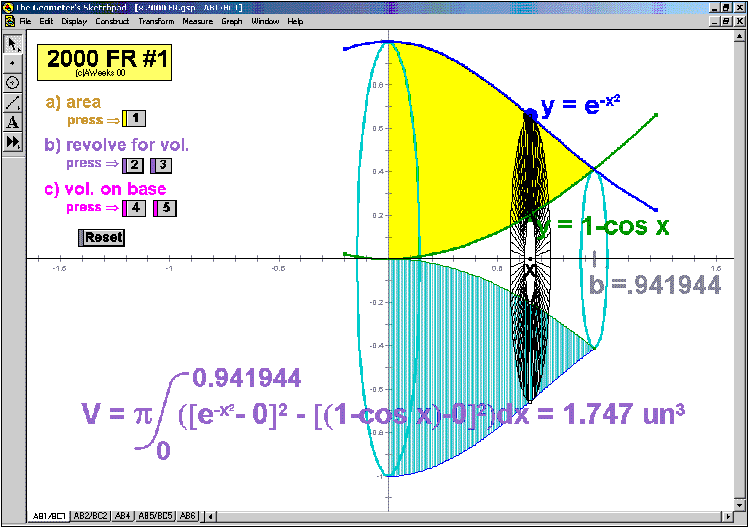
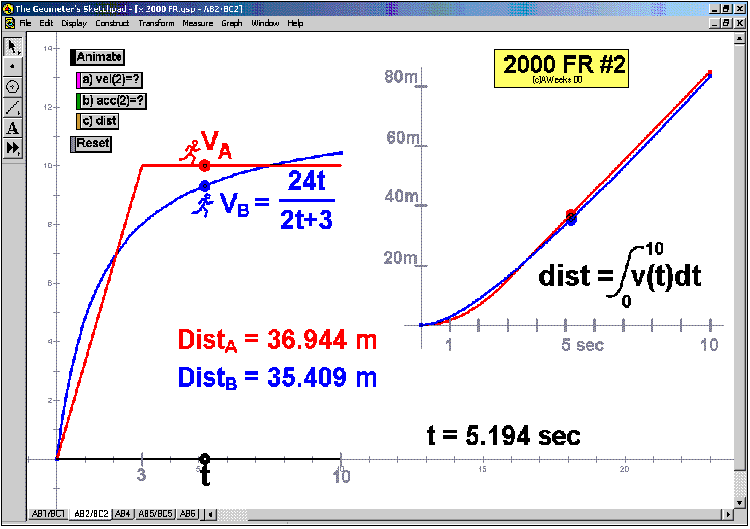
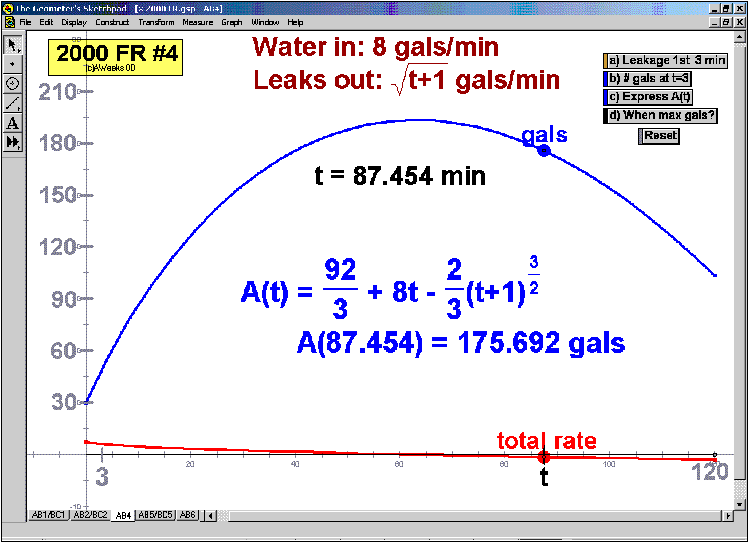
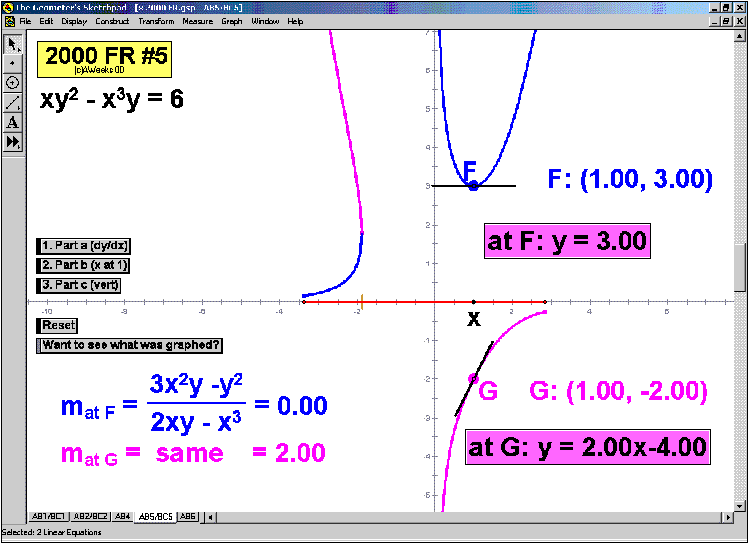
2000 animations to AP Calculus AB/BC Exams’ FRs
1999 animations to AP Calculus AB/BC Exams’ FRs
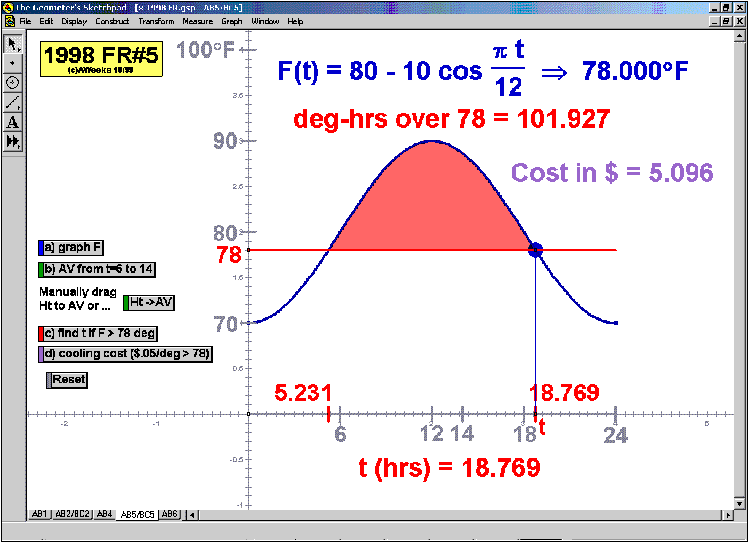
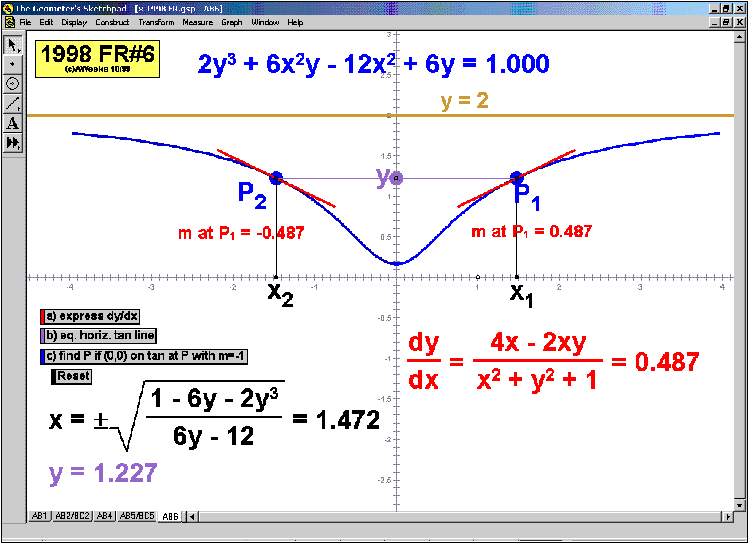
1998 animations to AP Calculus AB/BC Exams’ FRs
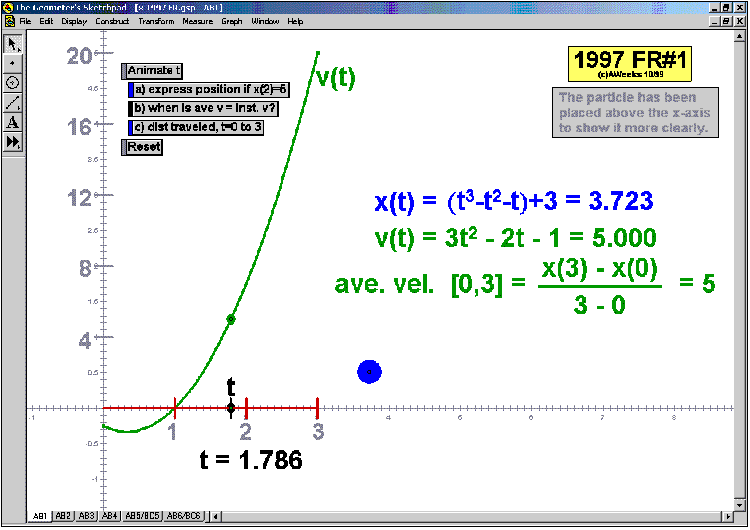
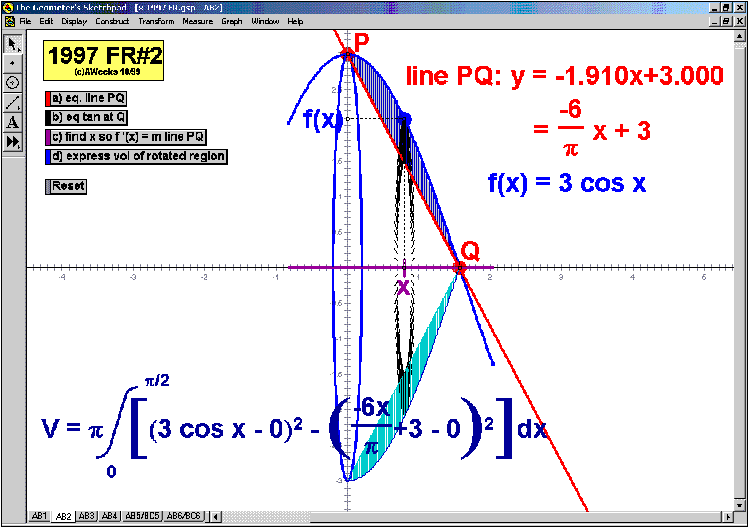
1997 animations to AP Calculus AB/BC Exams’ FRs