PLEASE NOTE: Calculus In Motion and Algebra In Motion animations are NOT videos. They are the actual animation files YOU get to interact with yourself. The videos on this page show quick views of a few of the animations in use. Each video has been restricted to be under 3 minutes (most just 1 or 2 minutes). So, to reveal as much information as possible, features are displayed very rapidly – MUCH faster than “classroom pace”. These videos provide just a glimpse of the actual power and capabilities of the animations. Screen capture software to create videos noticeably affects the running of the animations. The actual animations run smoother and sharper on their own. In the actual animations, a Motion Controller can be accessed to control the speed of any animation as desired. AB/BC Calculus Exam Free Response Question animations continue to be added each year and continue to be constructed in the same way as the 6 years of video samples below.
CALCULUS IN MOTION™
308 animations of nearly every concept in a first year calculus course including animations of 2025-1997 released AP Exam AB & BC Free Response Questions
CLICK BELOW for a quick VIDEO peek at a cluster of animations for …
Derivatives (def, graphs, rel rates, MVT, slope fields, etc)
Integrals (def, Riemann Sums, area, MVT, arc length)
Volumes by Revolution
Volumes on a Base
AB/BC Calculus Exam Free Response Questions --- 2019, 2018, 2017, 2016, 2015, 2014
* * * (Subsequent AP Exam FRQ animations through 2025 have been written in the same manner as shown in the 6 years of videos posted above.)
Jump ahead to more calculus videos.
ALGEBRA IN MOTION™ (GEOMETRY included too!)
224 animations of key topics in: (all in one set)
Pre-Algebra, Algebra 1, Geometry, Algebra 2, Trigonometry, Pre-Calculus
CLICK BELOW for a quick VIDEO peek at a cluster of animations for …
Algebra 1
Geometry - New in 2016
Algebra 2
Conics
Trigonometry
Pre-Calculus
Jump ahead to more algebra videos.
****
More Videos of Calculus In Motion in use (single animation files)
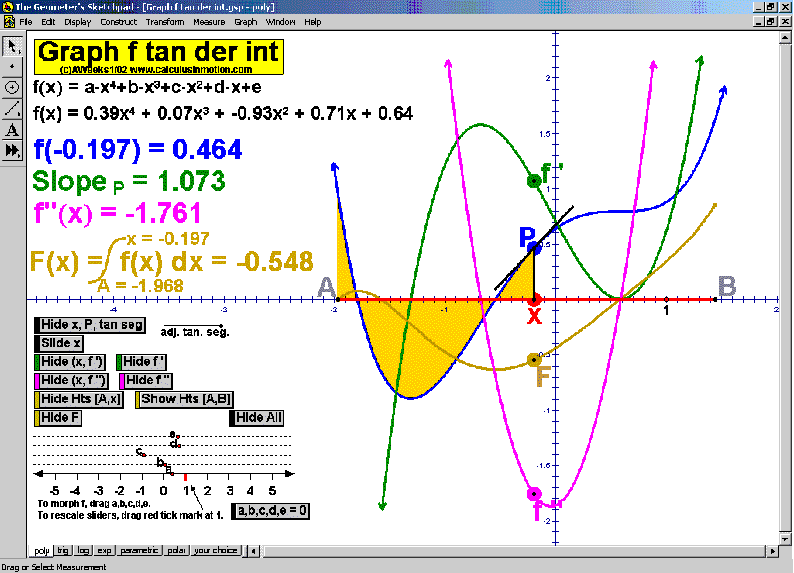
Graph f, Tangent, Derivative, Integral (Calculus In Motion)
Interact with graphs including sliding tangents, 1st and 2nd derivatives, and the integral as an accumulation of heights. Pages cover polynomials, trig, exp, ln, parametric, polar, and any curve of your own choosing. Morph the original curve to see the effects on the other components.
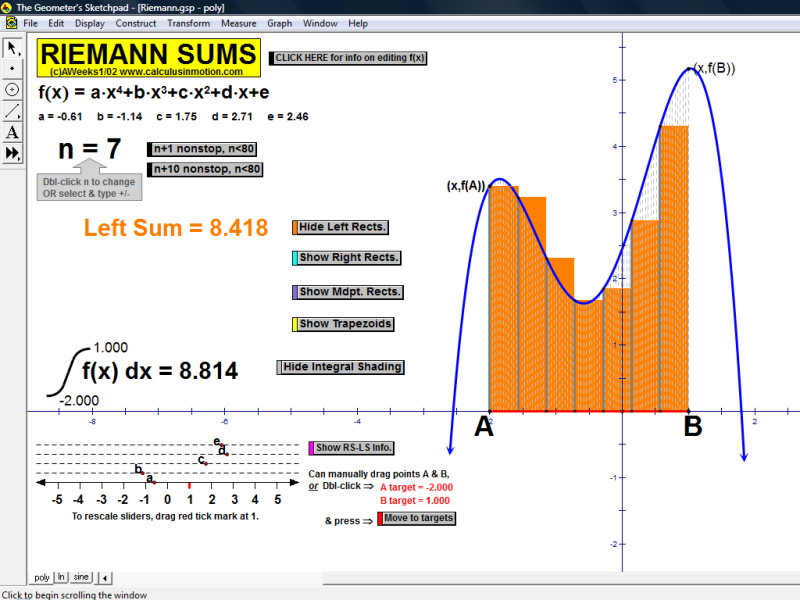
Riemann Sums (Calculus In Motion)
Choose 1 to 80 subdivisions of interval [A,B] and approximate the integral using rectangles for left sums, right sums, or midpoints; or use trapezoids for the Trapezoidal Rule. Change the domain, morph the function, or use the examples on the other pages of the file.
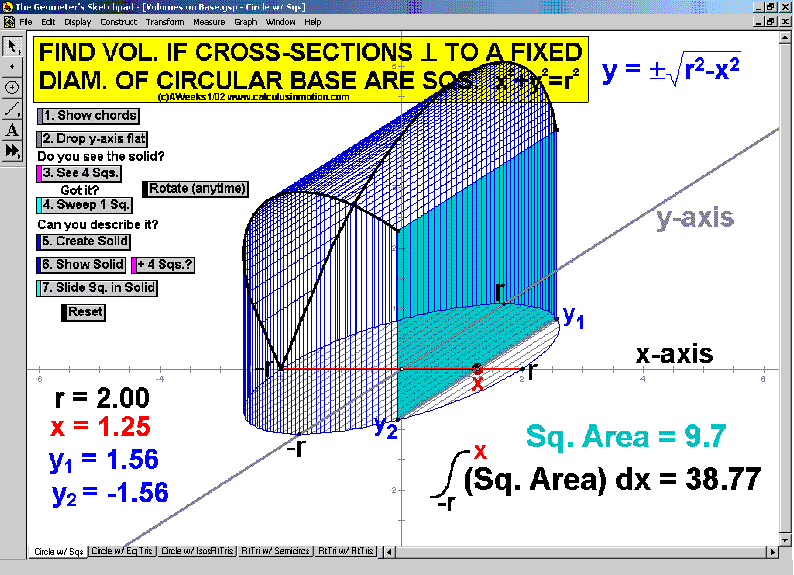
Volumes on a Base (Calculus In Motion)
This classic problem is one of several that walk through the visualization of these difficult shapes one step at a time. Afterwards, students are able to transfer what they have learned to new bases and new cross-sections.
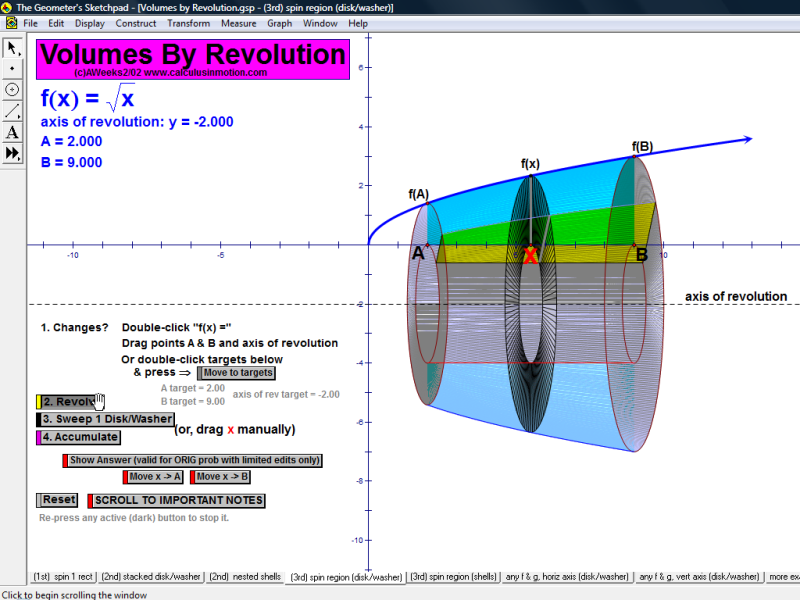
Volumes by Revolution (Calculus In Motion)
Build this concept in 3 stages. First, spin a single isolated rectangle. Second, revolve a discrete number of rectangles determined by the curve which would approximate the solid’s volume. Third, revolve the entire region (infinitely many, infinitely thin rectangles). Use any function, any horizontal or vertical axis of revolution, any partitioning, any interval. Then sweep a cross-section through the solid which would give the exact volume via integration. This video demo shows the disk/washer technique, but the same file also has pages presenting an identical development of the shell method.

Slope Fields (Calculus In Motion)
First, develop the meaning of a slope field by gliding a dynamic “slope column” across the graph of f ‘. See one tangent segment “pilot” the field & create the graph of f. Desired differential equations can be entered & many more features can be explored (e.g. Euler’s Method).
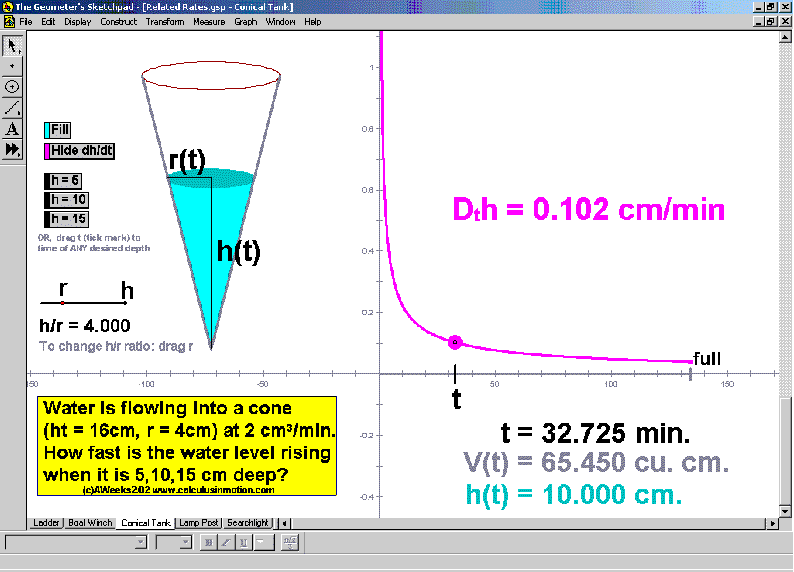
Related Rates – the classics (Calculus In Motion)
As a cone fills with water, analyze the change in the rate of increase of the water’s depth for various instants and various cones. Four other classic animations are in this file as well.
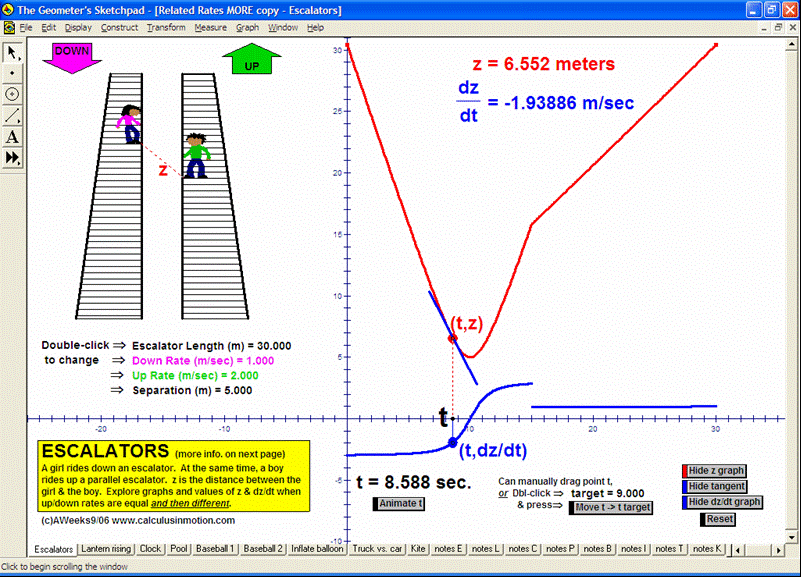
Related Rates – more (Calculus In Motion)
This file has 9 more related rates animations exploring escalators (seen in the video), a clock, a pool, vehicles approaching an intersection, baseball, a balloon, a kite, etc.
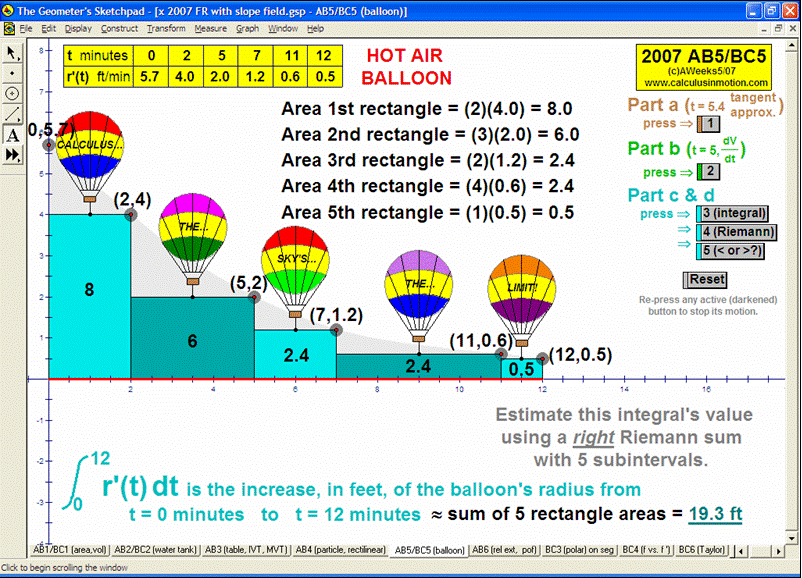
animation to 2007 AP Calculus Exam Free Response Question AB5/BC5 (Calculus In Motion)
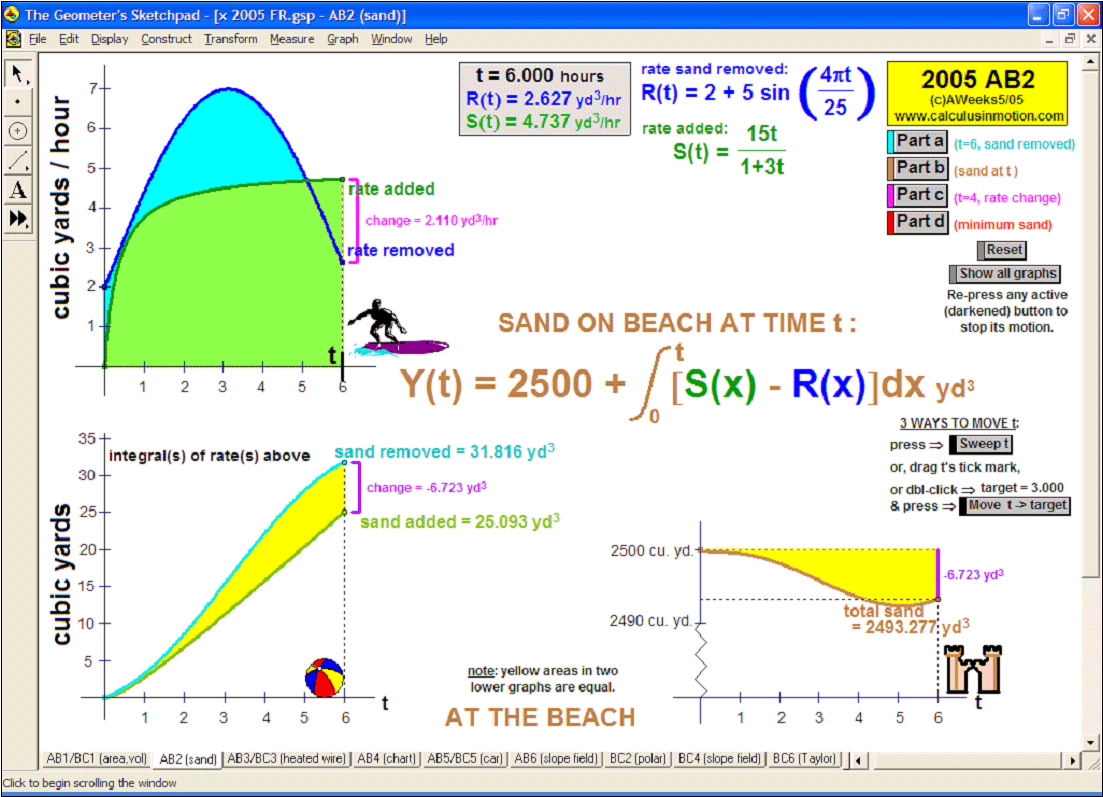
animation to 2005 AP Calculus Exam Free Response Question AB2 (Calculus In Motion)
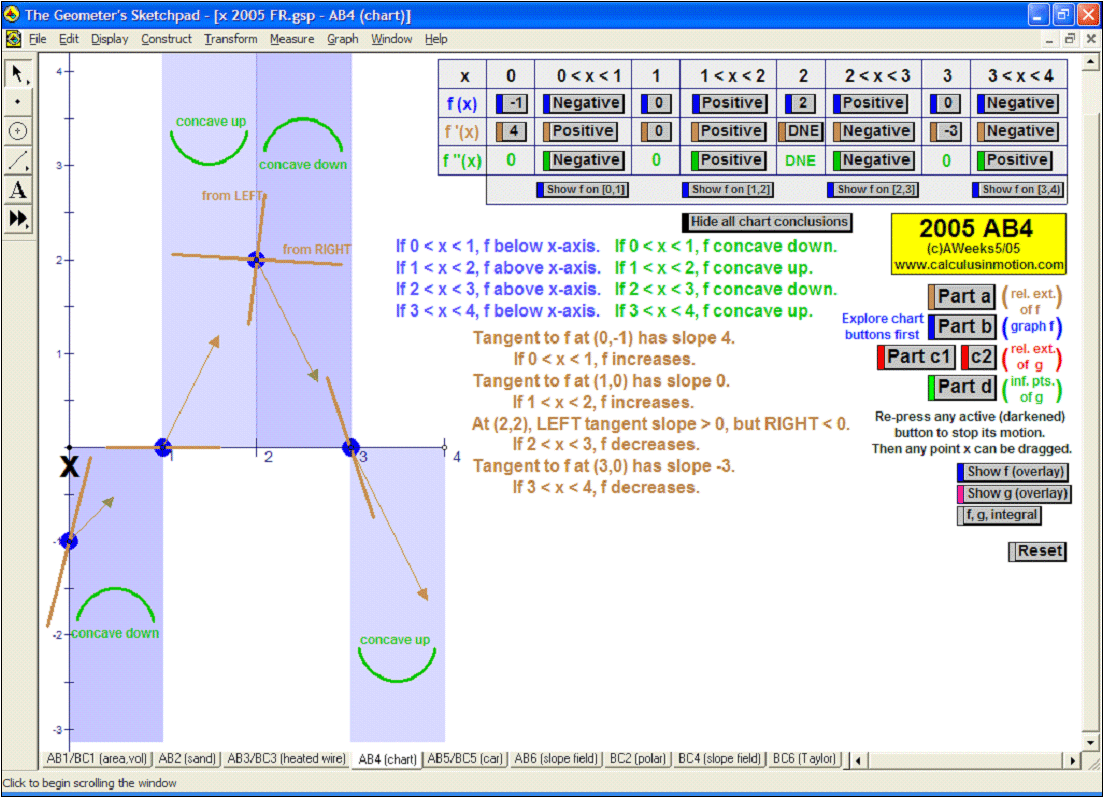
animation to 2005 AP Calculus Exam Free Response Question AB4 (Calculus In Motion)
****
More Videos of Algebra In Motion in use (single animation files)
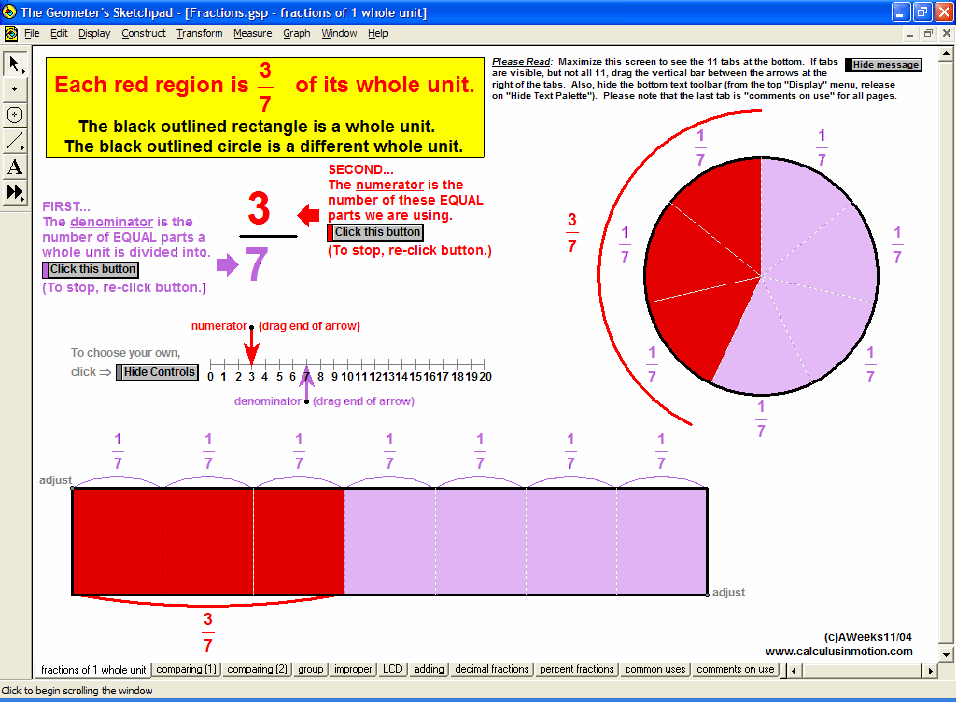
Fractions (Algebra In Motion)
Interact with graphs including sliding tangents, 1st and 2nd derivatives, and the integral as an accumulation of heights. Pages cover polynomials, trig, exp, ln, parametric, polar, and any curve of your own choosing. Morph the original curve to see the effects on the other components.
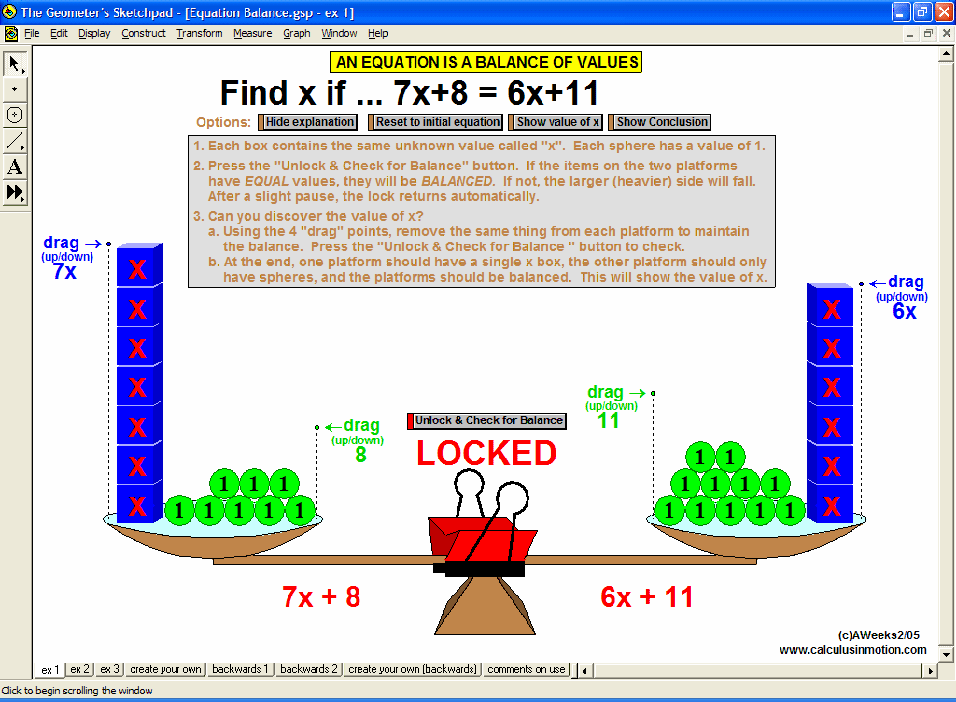
Equation Balance (Algebra In Motion)
Connect equation solving with the concept of balance. Interact with the scales to discover the value of x in each blue box. Use preset examples or create your own. Also, reverse the process, if desired.

Coordinate Plane Basics (Algebra In Motion)
Demonstrate the basic coordinate plane vocabulary and explore the connections between an ordered pair and its point’s location as points are dragged around the plane.
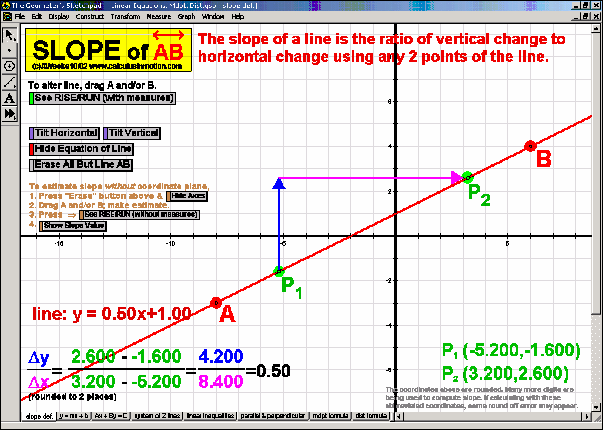
Linear Equations, Distance, Midpoint – Slope (Algebra In Motion)
Create a visual rise/run on any line and interact with it learn the critical concept of slope. Mention is also made of other pages of this file that address other topics of linear equations.
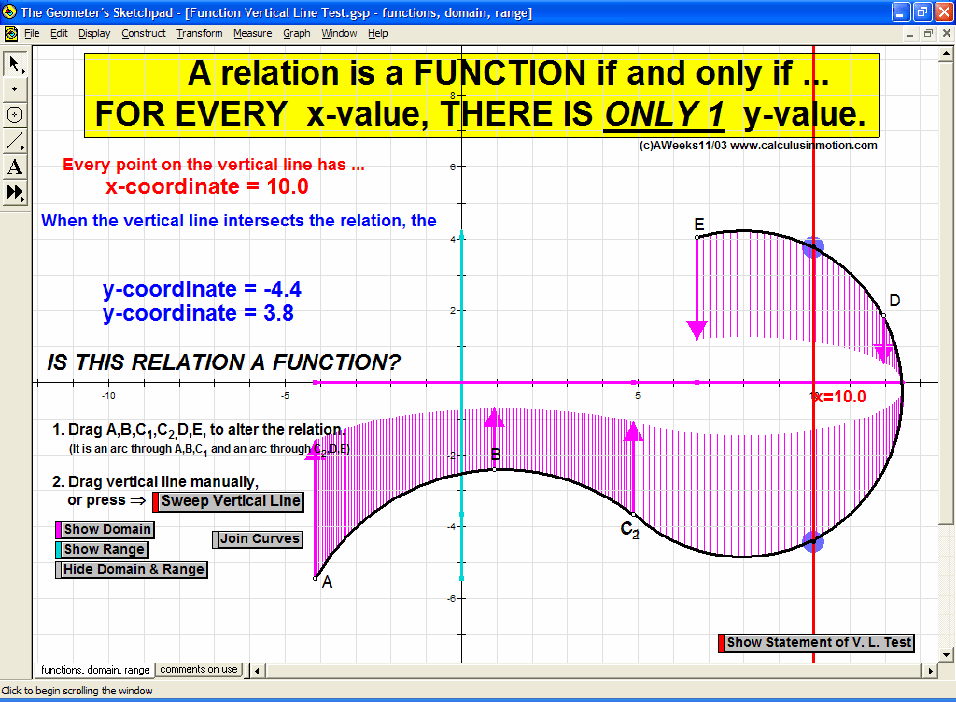
Function Vertical Line Test, Domain & Range (Algebra In Motion)
Sweep a vertical line across changeable relations to explore the definition of a function. Other buttons demonstrate the meaning of domain and range.
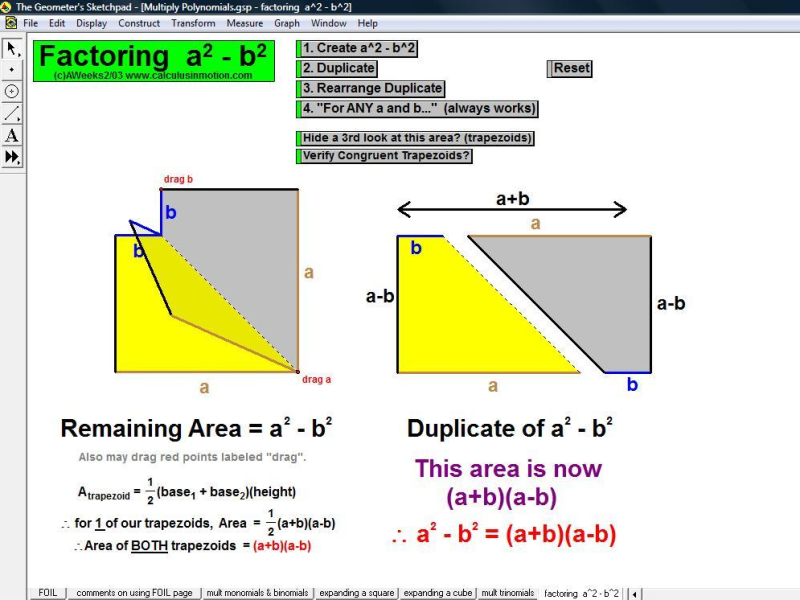
Multiplying Polynomials – Factor Difference of 2 Squares (Algebra In Motion)
Provide a concrete model for the factored form of the difference of two squares.

Conic Sections (Algebra In Motion)
Create the conic sections from their definitions. Explore their graphs, equations, eccentricity, and how it is that they can all come from the same general equation.
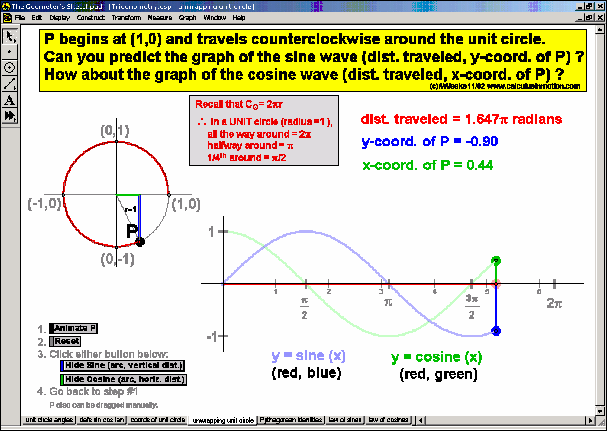
Trigonometry Animations (Algebra In Motion)
Here’s a brief look at 4 of the many trigonometry animations – basic rotation; definitions of the sine, cosine, and tangent ratios; special angles on the unit circle with reference triangles, and unwrapping the unit circle into the sine and cosine graphs.
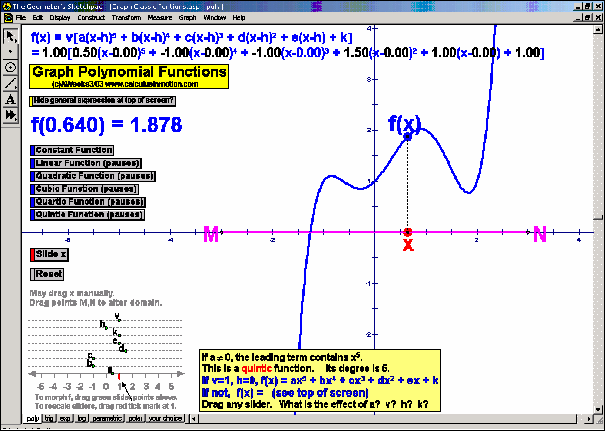
Graph Classic Functions (Algebra In Motion)
Interact with the graphs of various functions (polynomial, trigonometric, exponential and logarithmic) as well as parametric and polar graphs (plus anything you wish to invent). Each can be morphed by dragging coefficient values.
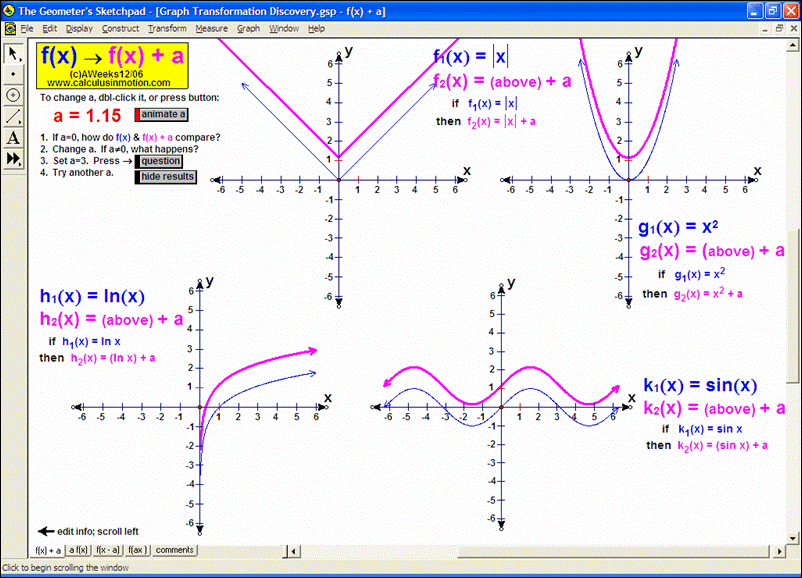
Graph Transformation Discovery (Algebra In Motion)
Discover how f(x) compares to f(x)+a, af(x), f(x-a), and f(ax) by interacting with “a” and choosing any 4 functions you desire.

Vertical Team – Open Box (Algebra In Motion)
Explore the characteristics of an open box folded from a rectangular piece of material with squares removed from its corners. Suitable for many different math courses.